Straight Lines Formulas for NDA 

Straight Lines

A straight line can be described as an infinite, one-dimensional object with no width. It consists of an unbroken series of points that continue indefinitely in both directions. The line is formed by connecting an infinite number of these points in a way that they align perfectly with no curves or bends along its length

What is a Straight Line?

A straight line is a line that continues indefinitely in both directions without any deviation or curvature. It represents the simplest and most direct path between any two points along its length, and it does not exhibit any changes in direction or shape.

Types of Straight Lines

Straight lines can be further classified into three different types based on their orientation and direction: horizontal lines, vertical lines, and oblique or slanting lines.

Horizontal lines: These lines are drawn parallel to the horizon or the x-axis in a two-dimensional Cartesian coordinate system. They have a constant y-coordinate and do not slope or incline in the vertical direction.

Vertical lines: These lines are drawn perpendicular to the horizon or the y-axis in a two-dimensional Cartesian coordinate system. They have a constant x-coordinate and do not slope or incline in the horizontal direction.

Oblique or slanting lines: These lines are neither horizontal nor vertical and have a slanted or tilted position. They have a non-zero slope and can be drawn at various angles relative to the x- and y-axes in a Cartesian coordinate system.

Properties of a Straight Line

The properties of straight lines are mentioned below:

Infinite Length: A straight line extends indefinitely in both directions and has infinite length..

Zero Area and Volume: Despite its infinite length, a straight line has zero area and zero volume. It is a one-dimensional object with no width or depth.

One-Dimensional Figure: A straight line is a one-dimensional geometric figure. It is characterized by its extension along a single dimension.

Multiple Lines Through a Point: An infinite number of lines can pass through a single point. Every point on a plane can be connected to the given point, forming a line.

Equation of a Straight Line

The general equation of a straight line can be given as ax + by + c = 0, where

• a, b, c are constants, and
• x, y are variables.

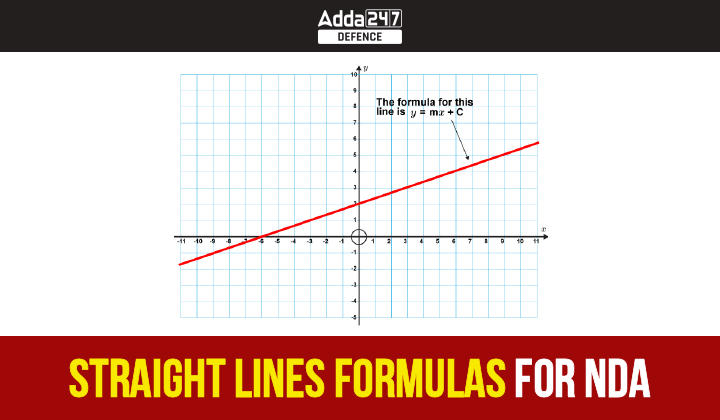
Slope:

The equation of a straight line in slope-intercept form is given by:

y = mx + c

where, ‘m’ denotes the slope of the line, and ‘c’ is the y-intercept.

Slope and Y-intercept Form

A straight line having slope m = tanθ where θ is the angle formed by the line with the positive x-axis, and y-intercept as b is given by: y = mx + b, where m is the slope.

Slope Point Form

A straight line having slope m = tanθ where θ is the angle formed by the line with the positive X-axis, and passing through a point (x1, y1) is given by:

Slope Point Form as: y – y1 = m(x – x1)

Two Point Form

A straight line passing through points (x1 , y1) and (x2 , y2) is given in the two point form as: y – y1 = [(y2 – y1) / (x2 – x1)] (x – x1).

Intercept Form

Consider a straight line that intersects the x-axis at point A, which has coordinates (a, 0), and intersects the y-axis at point B, which has coordinates (0, b). We can express the equation of this line using the Intercept Form.

In the Intercept Form, the equation is given by x/a + y/b = 1. Here, “a” represents the x-intercept, which is the x-coordinate of the point A where the line crosses the x-axis. Similarly, “b” represents the y-intercept, which is the y-coordinate of the point B where the line crosses the y-axis.

Straight Lines Examples

Example 1: For the straight line y = -3x + 2, what are: a) the slope b) the y-intercept?

Solution: a) The slope: The slope of a line is represented by the coefficient of x in the equation. In this case, the coefficient of x is -3. Therefore, the slope of the line y = -3x + 2 is -3.

2. b) The y-intercept: The y-intercept is the point where the line intersects the y-axis. In the equation y = -3x + 2, we can see that the constant term is 2. This means that when x is 0, y takes the value of 2. Thus, the y-intercept of the line is 2.

Example 2: Find the equation of a straight line that has y-intercept 4 and is perpendicular to straight line joining (2, -3) and (4, 2).

The slope of a line is calculated using the formula:

slope = (y2 – y1) / (x2 – x1),

where (x1, y1) and (x2, y2) are the coordinates of two points on the line.

Using the coordinates (2, -3) and (4, 2), we can calculate the slope:

slope = (2 – (-3)) / (4 – 2) = 5 / 2.

Since we are looking for a line perpendicular to this line, the slope of the new line will be the negative reciprocal of 5/2.

The negative reciprocal of 5/2 is -2/5.

Now we have the slope of the perpendicular line, -2/5, and the y-intercept, 4.

Using the slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept, we can substitute these values into the equation:

y = (-2/5)x + 4.

Example 3: What is the equation of a straight line parallel to the y-axis and passing through the point (4,−2)?

A line parallel to the y-axis is vertical and has an undefined slope since it does not have any horizontal change. Such a line is of the form x = c, where “c” is a constant representing the x-coordinate of any point on the line.

In this case, we are looking for a line parallel to the y-axis passing through the point (4, -2). Since the line is parallel to the y-axis, its x-coordinate remains constant and equal to 4.

Therefore, the equation of the line parallel to the y-axis and passing through the point (4, -2) is x = 4.

Example 4: What is the equation of the straight line which is perpendicular to y=x and passes through (3, 2)?

To find the equation of a straight line that is perpendicular to the line y = x and passes through the point (3, 2), we need to determine the slope of the given line first.

The line y = x has a slope of 1 because it is in the form y = mx, where m represents the slope.

To find the slope of a line perpendicular to y = x, we need to take the negative reciprocal of the slope. So, the perpendicular line will have a slope of -1.

Now, we have the slope of the perpendicular line (-1) and the point it passes through (3, 2).

Using the point-slope form of a line, which is y – y1 = m(x – x1), we can substitute the values:

y – 2 = -1(x – 3).

Simplifying the equation further:

y – 2 = -x + 3.

Now, let’s rearrange the equation to obtain the slope-intercept form (y = mx + b):

y = -x + 3 + 2,

y = -x + 5.

Therefore, the equation of the straight line perpendicular to y = x and passing through the point (3, 2) is y = -x + 5.