Table of Contents
भूमितीचे सूत्र | Geometry Formulas
भूमितीचे सूत्र | Geometry Formulas : परिमिती, क्षेत्रफळ आणि भौमितिक आकारांचे आकारमान यांसारखे परिमाण आणि संबंधित गुणधर्म शोधण्यासाठी भूमिती सूत्रे वापरली जातात. विज्ञान आणि तंत्रज्ञानाच्या विविध क्षेत्रात ही सूत्रे मोठ्या प्रमाणावर वापरली जातात. या लेखात, आम्ही त्रिकोण, चौकोन, आयत इत्यादी काही मूलभूत आकारांसाठी मूलभूत भूमिती सूत्रांसह 2D आणि 3D भूमितीची सर्व सूत्रे समाविष्ट करू. ही सूत्रे इच्छुकांना स्पर्धात्मक परीक्षांच्या तयारीसाठी देखील मदत करेल.
भूमितीचे सूत्र | Geometry Formulas : विहंगावलोकन
भूमितीची सूत्रे भौमितिक आकाराचे वेगवेगळे गुणधर्म शोधण्यासाठी वापरली जातात. हे गुणधर्म लांबी, रुंदी किंवा उंची (3D आकारांच्या बाबतीत), क्षेत्रे, परिमिती आणि खंड (3D भौमितिक आकृत्यांच्या बाबतीत) सारखे परिमाण असू शकतात.
| भूमितीचे सूत्र | Geometry Formulas : विहंगावलोकन | |
| श्रेणी | अभ्यास साहित्य |
| उपयोगिता | आदिवासी विकास विभाग भरती आणि इतर सर्व स्पर्धा परीक्षांसाठी उपयुक्त |
| विषय | गणित |
| लेखाचे नाव | भूमितीचे सूत्र | Geometry Formulas |
| लेखातील प्रमुख मुद्दे |
|
भूमिती सूत्रे
- भूमितीची सूत्रे भौमितिक आकाराचे वेगवेगळे गुणधर्म शोधण्यासाठी वापरली जातात. हे गुणधर्म लांबी, रुंदी किंवा उंची (3D आकारांच्या बाबतीत), क्षेत्रे, परिमिती आणि आकारमान (3D भौमितिक आकृत्यांच्या बाबतीत) सारखे परिमाण असू शकतात. गणितामध्ये, भूमिती म्हणजे बिंदू, रेषा, कोन, पृष्ठभाग, घन पदार्थांचे मोजमाप आणि त्यांचे गुणधर्म यांच्यातील संबंधांचा अभ्यास. भूमितीची शाखा स्थूलपणे दोन श्रेणींमध्ये वर्गीकृत केली जाऊ शकते: 2D भूमिती (द्विमितीय भूमिती) आणि 3D भूमिती (तीन आयामी भूमिती).
- 2D भूमितीमध्ये आपण 2D आकारांचा म्हणजेच द्विमितीय आकारांचा अभ्यास करतो. या भौमितीय आकृत्यांना फक्त दोन परिमाणे आहेत- लांबी आणि रुंदी (रुंदी). म्हणून, आपण या आकारांचे क्षेत्रफळ आणि परिमिती शोधू शकतो परंतु तिसरे परिमाण नसल्यामुळे त्यांचे आकारमान निश्चित केले जाऊ शकत नाही. 2D भौमितिक आकृत्यांची काही उदाहरणे म्हणजे त्रिकोण, चौरस, वर्तुळ, आयत इ.
- 3D भूमिती त्रिमितीय भूमितीय आकृत्यांच्या अभ्यासाशी संबंधित आहे. या भौमितिक आकारांना तीन परिमाणे आहेत – लांबी, रुंदी (रुंदी), आणि उंची (ज्याला खोली किंवा जाडी देखील म्हणतात). तिसऱ्या मितीच्या उपस्थितीमुळे, आम्ही क्षेत्रफळ आणि परिमिती शोधण्याव्यतिरिक्त भूमिती सूत्रांचा वापर करून 3D आकारांची मात्रा मोजू शकतो. 3D भौमितिक आकृत्यांची काही उदाहरणे म्हणजे शंकू, गोल, सिलेंडर, घन इ.
भूमितीची सूत्रे
वास्तविक जगातील गणना आणि आर्किटेक्चरमधील भूमितीय सूत्राचे महत्त्व पाहता, विद्यार्थ्यांना ही सूत्रे शिकवली जातात. विद्यार्थी 2D आणि 3D आकारांचे क्षेत्रफळ आणि खंड मोजण्यासाठी वेगवेगळ्या भूमितीय सूत्रांचा अभ्यास करतात. काही महत्त्वाची भौमितिक सूत्रे खाली दिली आहेत.
क्षेत्रफळ सूत्र
- ट्रॅपेझियमचे क्षेत्रफळ = उंची × (समांतर बाजूंची बेरीज)/2
- समभुज चौकोनाचे क्षेत्रफळ = (1/2) × d1 × d2; जेथे d1 आणि d2 हे समभुज चौकोनाचे दोन कर्ण आहेत
- विशेष चतुर्भुजाचे क्षेत्रफळ = (1/2) × d × (h1 + h2); जेथे d हा कर्ण आहे आणि h1 आणि h2 हे शिरोबिंदूंपासून कर्णांवर काढलेले लंब आहेत.
- क्यूबॉइडचे पृष्ठभाग क्षेत्रफळ = 2(lb + bh + hl); जेथे l, b आणि h हे क्यूबॉइडची लांबी, रुंदी आणि उंची दर्शवतात.
- घनाचे पृष्ठभाग क्षेत्रफळ = 6s² ; जेथे s घनाच्या बाजूचे प्रतिनिधित्व करतो.
- सिलेंडरचे पृष्ठभाग क्षेत्रफळ = 2Πr(r + h); जेथे h उंची दर्शवतो आणि r सिलेंडरची त्रिज्या दर्शवतो.
- समभुज त्रिकोणाचे क्षेत्रफळ = s²(√3/4), जेथे s = समभुज त्रिकोणाची बाजू आहे.
- नियमित षटकोनाचे क्षेत्रफळ = (3 x √3 x a²)/2, जेथे a = नियमित षटकोनाची बाजू आहे.
घनफळ सूत्र
- घनफळाची मात्रा = l × b × h; जेथे l, b आणि h हे क्यूबॉइडची लांबी, रुंदी आणि उंची दर्शवतात.

- सिलेंडरची मात्रा = Πr² h; जेथे h उंची दर्शवतो आणि r सिलेंडरची त्रिज्या दर्शवतो.
- पोकळ सिलेंडरची मात्रा = Π. h(R² – r²), जेथे R = बाह्य त्रिज्या, r = अंतर्गत त्रिज्या.
- सामान्य चौरस पिरॅमिडचे आकारमान = (1/3) xhx s², जेथे s = चौरस पायाच्या एका बाजूची लांबी आणि h ही पिरॅमिडची उंची आहे.
मूलभूत भूमिती सूत्रे
मुलभूत भूमिती सूत्रे प्रत्येक व्यक्तीसाठी महत्वाची असतात मग ती कोणत्याही स्पर्धा परीक्षेची तयारी करत असेल. या सूत्रांचे अभियांत्रिकीपासून ते सांख्यिकीपर्यंत जवळपास सर्वच क्षेत्रांमध्ये अर्ज आहेत. विविध सरकारी आणि खाजगी नोकऱ्यांच्या योग्यता विभागात या सूत्रांबद्दलच्या संकल्पना विचारल्या जातात. 2D आणि 3D भूमितीय आकृत्यांशी संबंधित ही मूलभूत सूत्रे येथे नमूद केली आहेत.
- चौरसाची परिमिती = 4 × बाजू
- आयताची परिमिती = 2 × (लांबी + रुंदी)
- चौरसाचे क्षेत्रफळ = बाजू²
- आयताचे क्षेत्रफळ = लांबी × रुंदी
- त्रिकोणाचे क्षेत्रफळ = ½ × पाया × उंची
- ट्रॅपेझॉइडचे क्षेत्रफळ = ½ × (बेस₁ + बेस₂) × उंची
- वर्तुळाचे क्षेत्रफळ = A = π × r²
- वर्तुळाचा घेर = 2πr
- सिलेंडरचे वक्र पृष्ठभागाचे क्षेत्रफळ = 2πrh
- सिलेंडरचे एकूण पृष्ठभाग क्षेत्रफळ = 2πr(r + h)
- सिलेंडरची मात्रा = V = πr²h
- शंकूचे वक्र पृष्ठभागाचे क्षेत्रफळ = πrl
- शंकूचे एकूण पृष्ठभाग क्षेत्रफळ = πr(r + l) = πr[r + √(h² + r²)]
- शंकूचे आकारमान = V = ⅓ × πr²h
- गोलाचे पृष्ठभाग क्षेत्रफळ = S = 4πr²
- गोलाची मात्रा = V = 4/3 × πr³
वरील सर्व सूत्रांमध्ये,
- h उंचीशी संबंधित आहे,
- r त्रिज्येशी संबंधित आहे,
- l = तिरकी उंची.
2D भूमिती सूत्रे
आपल्याला माहित आहे की, 2D भौमितिक आकृत्या म्हणजे त्या आकृत्या ज्यांना फक्त दोन मिती आहेत. या आकृत्यांच्या विविध गुणधर्मांची गणना करण्यासाठी सूत्र जाणून घेणे अत्यंत महत्त्वाचे आहे. या उद्देशासाठी, खाली आम्ही सर्व संबंधित 2D भूमिती सूत्रांचा उल्लेख केला आहे.

3D भूमिती सूत्रे
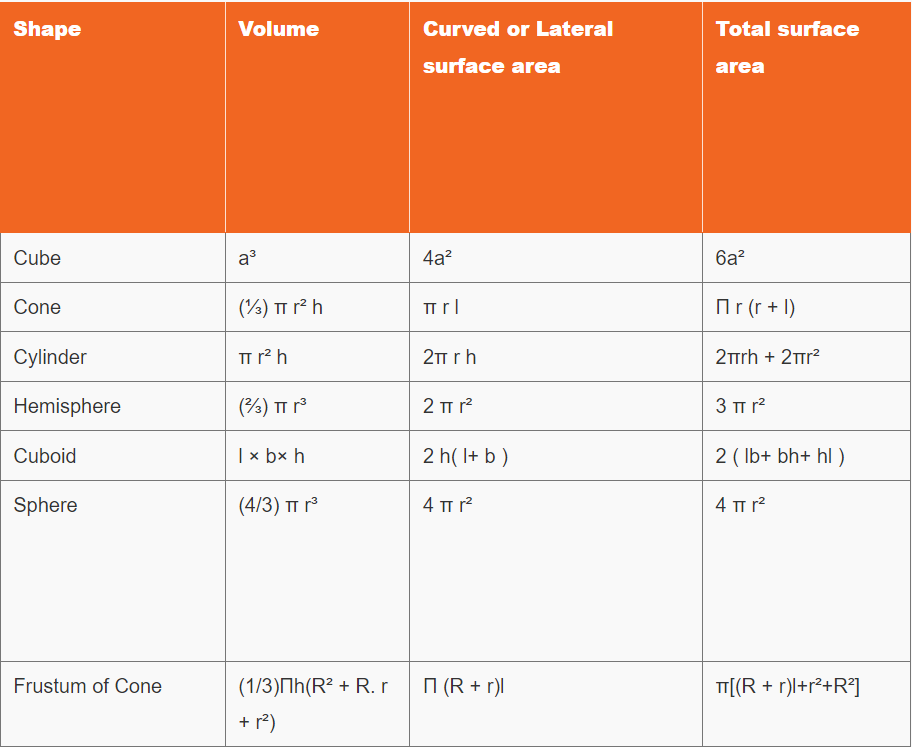
3D आकारांना असे नाव देण्यात आले आहे कारण त्यामध्ये लांबी, रुंदी आणि उंची असे तीन आयाम असतात. निसर्गात थ्रीडी आकार सर्वत्र आढळतात. म्हणून, वास्तविक-जगातील समस्या सोडवण्यासाठी, ही सूत्रे शिकणे अत्यंत महत्त्वाचे आहे. म्हणून, आम्ही खाली सर्वात उपयुक्त 3D भूमिती सूत्रांचे सारणीबद्ध केले आहे.
महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळावा.








