Fact and Formulae based Mathematics Notes For CTET Exam, Download PDF

Mathematics is an equally important section for CTET, KVS & DSSSB Exams and has even more abundant importance in some other exams conducted by central or state govt. Generally, there are questions asked related to basic concepts, Facts, and Formulae.

To let you make the most of the Mathematics section, we are providing important facts related to the Facts and Formulae. At least 2-3 questions are asked from this topic in most of the teaching exams. We wish you all the best of luck to come over the fear of the Mathematics section.

Facts and Formulae

• 0 is neither a prime number nor a composite number.
• 0 is neither a negative number nor a positive number.
• 1 is the only natural number that is neither a prime number nor a composite number.
• 1 is the smallest natural number.
• -1 is the largest negative integer.
• 2 is the only even prime number.
• The unit’s digit of any perfect square number must be 0,1,4, 5, 6, or 9.
• The unit’s digit of the square of a number whose unit’s digit is 0 will be 0.
• The unit’s digit of the square of a number whose unit’s digit is 1 or 9 will be 1.
• The unit’s digit of the square of a number whose unit’s digit is 2 or 8 will be 4.
• The unit’s digit of the square of a number whose unit’s digit is 3 or 7 will be 9.
• The unit’s digit of the square of a number whose unit’s digit is 4 or 6 will be 6.
• Sum of numbers from 1 to n = n(n+1)/2 Example: Sum of the first 5 natural numbers = 5(5+1)/2= 15
• Number of odd numbers from 1 to n = ((Last odd number +1))/2 Example: Number of odd numbers from 1 to 99 = (99+1)/2=50
• Number of even numbers from 1 to n = (Last even number)/2, Example: Number of even numbers from 1 to 50 = 50/2=25
• Sum of even numbers from 1 to n = Number of even numbers × (Number of even numbers + 1), Example: Number of even numbers from 1 to 50 =  50/2=25 ∴ Sum of even numbers from 1 to 50 =  50/2=25(25+1)=650

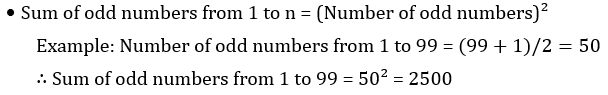
Properties of Numbers

The product of two consecutive numbers is divisible

• The product of two consecutive numbers is divisible by 2. For example, 4 × 5 = 20, which is divisible by 2.
• The product of three consecutive numbers is divisible by 6. For example, 3 × 4 × 5 = 60, which is divisible by 6.
• The product of four consecutive numbers is divisible by 24. For example, 3 × 4 × 5 × 6 = 360, which is divisible by 24.
• The product of five consecutive numbers is divisible by 120. For example, 3 × 4 × 5 × 6 × 7 = 2520, which is divisible by 120.
• The product of ‘n’ consecutive numbers is divisible by 1 × 2 × 3 × …… × n. For example, the product of ten consecutive numbers will divisible by 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10.
• The difference between the squares of two consecutive numbers is always equal to the sum of both numbers. For example, 16² – 15² = 16 + 15 = 31
• The difference between the square of two consecutive odd numbers is always a multiple of 8. For example, 17² – 15²= 289 – 225 = 64
• The sum of the first ‘n’ odd numbers is the square of ‘n’. For example, the sum of the first five odd numbers = 1 + 3 + 5 + 7 + 9 = 5²= 25

Sharing is caring!