Q.2. Does the Trapezium have parallel sides?

Ans: Yes, the Trapezium is a four-sided figure with one pair of parallel sides.

Q.3. Are the diagonals of a Trapezium equal?

Ans: No, the diagonals of a Trapezium are not equal because all the four sides are not equal in a Trapezium.

Q.4. What is the perimeter of a Trapezium?

Ans: The perimeter of a Trapezium is the sum of all the sides of a Trapezium.

Q.5. What is the altitude of a Trapezium?

Ans: The perpendicular distance between the parallel sides of a Trapezium is known as the altitude or height of a trapezoid.

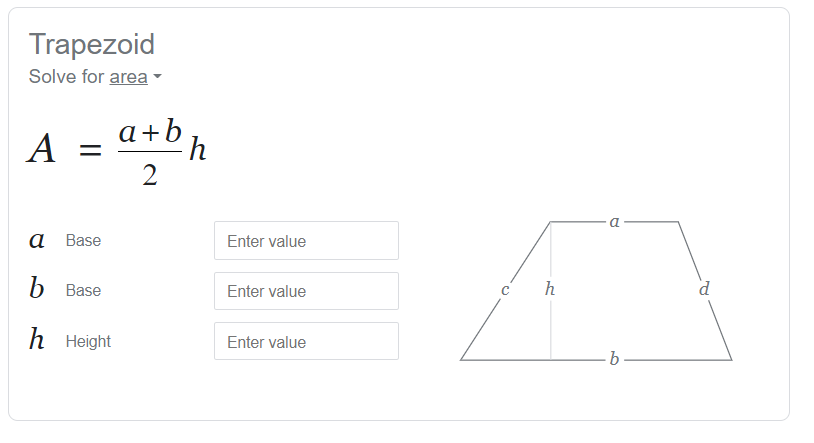
Area of Trapezium Formula in Maths

Q: Q.1. What is the area of a Trapezium formula?

Ans: Area of a Trapezium =1/2×(Sum of parallel sides)×Distancebetweentheparallelsides

Table of Contents

Area of Trapezium

It is a region covered by a 2-dimensional shape in a plane. It is the space enclosed in 2D geometry and measured in square units (like cm², m², in², etc). Alike other geometrical shapes, Trapezium also has its own properties and formulas based on area and perimeter. Hence, the area of the Trapezium formula is explained below along with its derivation and examples to make you understand better.

Let us see the formula to understand how to calculate the area of the Trapezium.

Area of Trapezium Formula

Trapezium area can be calculated by using the below formula:

Area of Trapezium = 1/2 x distance between the parallel sides x Sum of parallel sides

Area = 1/2 x h x (AB + DC)

Where,

“a” and “b” are the bases, and

“h” is the altitude or height or distance between parallel sides.

Perimeter of Trapezium

The perimeter of a shape is defined as the total length of its boundary. The perimeter of a shape is determined by adding the length of all the sides and edges enclosing the shape. It is measured in linear units of measurement like centimeters, meters, inches, or feet.

The perimeter of the Trapezium can be calculated by using the mentioned formula:

Perimeter = Sum of all the sides = AB + BC + CD + DA

Trapezium

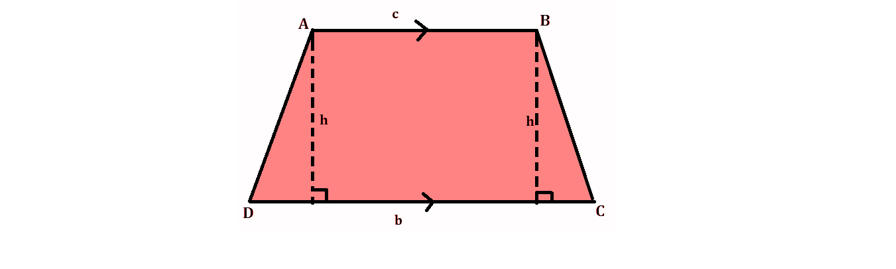
The area of Trapezium is a region covered by a 2-dimensional shape in a plane. A quadrilateral with at least one pair of parallel sides is called, in American and Canadian English, a Trapezoid. In British and other forms of English, a Trapezoid is called a Trapezium. It is a quadrilateral with exactly one pair of opposite sides parallel to each other and the other pair of a Trapezium are non-parallel. Euclidean Geometry defines a quadrilateral as a polygon with four sides and four vertices. When the trapezium is drawn it suggests a desk or a triangle, this is reduced from the top.

In the above figure, Sides AB and CD are parallel to each other (bases) whereas AD and BC are non-parallel sides (legs) and h denotes the height between two parallel lines.

Types of Trapezium

Types of Trapezium The trapezium is divided into 3 distinct classes as mentioned below:

Isosceles Trapezium
Right Trapezium
Scalene Trapezium

Isosceles Trapezium :

It can be defined as a Trapezium in which both legs and base angles are of the same measure.

Right Trapezium :

A right Trapezium is a Trapezium having two right angles.

Scalene Trapezium :

A scalene Trapezium is a Trapezium with no sides of equal measure.

Properties of Trapezium

Every Trapezium has the following properties:

One pair of opposite sides are parallel.
The two non-parallel sides are unequal except for the isosceles Trapezium.
Two pairs of adjacent angles add up to 180 degrees.
The diagonals intersect.
The line that joins the mid-points of the non-parallel sides is always parallel to the bases or parallel sides which is equal to half the sum of the parallel sides
The sum of the four interior angles is 4 right angles, i.e. 360⁰.
The sum of the four exterior angles is 4 right angles, i.e. 360⁰.

Trapezium Formula

The formula for the area of a trapezium (trapezoid) is:

A = \frac{1}{2} \times (a + b) \times ℎ

Where:

$ℎ$

You can use this formula to calculate the area of a trapezium when you know the lengths of the two parallel sides and the height.

How to Find Area of Trapezium

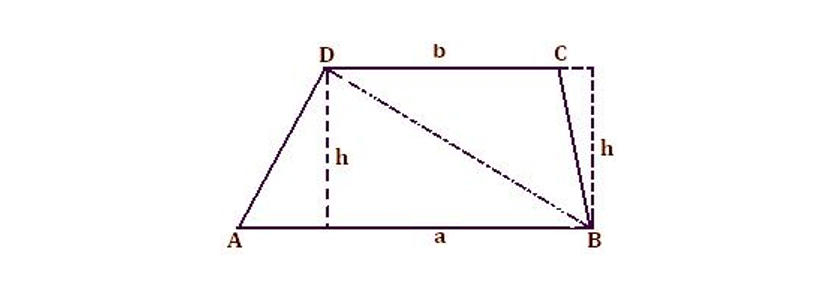
Here we will learn how to derive the formula to find the area of the Trapezium.

Area of Trapezium ABCD = Area of ∆ ABD + Area of ∆ CBD

= 1/2 × a × h + 1/2 × b × h

= 1/2 × h × (a + b)

= 1/2 (sum of parallel sides) × (perpendicular distance between them)

How to Find Area of Trapezium: Step-by-step process from Formula

Step 1: Find the dimensions of the given Trapezium, i.e., length of parallel sides and length of height.

Step 2: Add the length of parallel sides

Step 3: Multiply the sum of parallel sides with the height of the Trapezium

Step 4: Now, multiply the above-calculated value by 1/2 to get the final answer

The obtained value in step 4 is the area of the given Trapezium.

Some examples are given below for a better understanding of how to find out the area of the Trapezium.

Area of Trapezium- Uses

A Trapezium is a four-sided polygon. A Trapezium is having many applications in our daily life. In daily life, we can see the Trapezium shapes in the tabletops, bridge supporters, and architectural elements, in windows, doors, and in pencil boxes, handbags, etc. The concept of the Trapezium is used in physics to solve many problems. In mathematics, solving problems based on surface area or for finding the area and perimeter of complex figures. The formula of the Trapezium is used in the construction of the shape of the roof. A Trapezium has various applications in day-to-day life.

Area of Trapezium Formula Example Problems

Here, some questions are given below which will clear all your confusion.

Question 1:

Find the area of a Trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.

Solution:

Given,

a = 24 cm

b = 20 cm

Distance between two parallel sides, h = 15 cm

Area of a Trapezium =1/2×(Sum of parallel sides)×(Distance between them)

={1/2×(24+20)×15} cm²

=(1/2×44×15) cm²

=(22×15) cm²

=330 cm²

Hence, the area of the Trapezium is 330 cm².

Question 2:

What is the area of a Trapezium when bases are 12 cm and 20 cm respectively and the distance between the two parallel sides is 10 cm?

Solution:

Given,

a = 12 cm

b = 20 cm

Distance between two parallel sides, h = 10 cm

Area of a Trapezium =1/2×(Sum of parallel sides)×(Distance between them)

{1/2×(12+20)×10} cm²

=(1/2×32×10) cm²

=(16×10) cm²

=160 cm²

Hence, the area of the Trapezium is 160 cm².

Area of Trapezium Formula Practice Questions

Find the area of a Trapezium whose lengths of parallel sides are 10 cm and 6cm, respectively and the distance between the parallel sides is 5 cm.
If the area of a Trapezium is 728 cm². Find the height of the Trapezium such that the lengths of its parallel sides are 16 cm and 7 cm, respectively.
The area of a Trapezium is 384cm². If 3:5 is the ratio of the length of its parallel sides and the perpendicular distance between them is 12 cm. Find the length of each of the parallel sides.

Related Post: