Newton’s Laws of Motion Class 9- Know First, Second, Third Law

Newton’s Laws of Motion Class 9

In the field of physics, Newton’s laws of motion is a foundation of classic mechanics.  It gives us the idea of how an object behaves when it stands, moves or any force act on it and its response. There is a total of 3 laws of motion.  In 1687, these three laws were first compiled by  Sir Isaac Newton in his Philosophiae  Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy). Basically, these Newton’s Laws of Motion describe the relationship between force (which acts on an object or body) and motion ( Response of the object or body to that acting force). In this article, we will understand Newton’s laws and their explanations with examples and solve problems based on Newton’s laws of motion.

What is Newton’s Laws of Motion Class 9?

Newton’s laws of motion are fundamental principles that describe the relationship between the motion of an object and the forces acting upon it. Here are Newton’s three laws of motion, along with examples for each:

1. Newton’s First Law of Motion (Law of Inertia): “An object at rest tends to stay at rest, and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an external force.”Example: Imagine you’re sitting in a moving car, and suddenly the driver slams on the brakes. You’ll feel yourself being thrown forward. According to Newton’s first law, your body wants to keep moving forward (inertia). However, the car abruptly stops, applying an external force that causes your body to move in the direction opposite to the car’s motion.
2. Newton’s Second Law of Motion: “The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.”Mathematically, this law can be expressed as: F = m × a, where F is the net force applied to an object, m is its mass, and a is the resulting acceleration.Example: Consider two boxes, one with a mass of 2 kg and another with a mass of 5 kg. If you push both boxes with the same force, the lighter box will experience a greater acceleration than the heavier box. This is because the acceleration is inversely proportional to the mass according to Newton’s second law.
3. Newton’s Third Law of Motion: “For every action, there is an equal and opposite reaction.”This law states that whenever an object exerts a force on another object, the second object exerts an equal and opposite force on the first object.Example: Imagine a person standing on a skateboard. When they push against a wall with a certain force, according to Newton’s third law, the wall pushes back with an equal and opposite force. As a result, the person moves in the opposite direction due to the force exerted by the wall.

 

Newton’s First Law for Class 9

According to newton’s first law, A stationary object will remain stationary forever and a moving object will forever move in a straight line with constant momentum unless prevented from changing state by an externally applied force.

• From Newton’s first law we derive two very important concepts – (i) the inertia of matter and (ii) the definition of force.

Newton’s first law of Motion- The inertia of matter

The Characteristic for which a stationary object or body wants a stationary state or a moving object to maintain its state of motion or prevent it from changing its state is called inertia. The mass of matter is the measure of inertia.

•Interior is two types-
1. Interia of rest – A stationary object always remains in a stationary state. The tendency of matter to remain in a stationary state forever is called Interia of rest.

Example- When a car starts moving suddenly, the passenger sitting in the car is thrown backwards. This happens for stability. When the vehicle is stationary the passenger is also stationary i.e. all parts of the passenger’s body are stationary. When the car starts moving suddenly, the lower part of the passenger’s body moves with the car because it is adjacent to the car. But the upper body wants to stay still under the influence of static. So the passenger leans back.

2. Interia of the motion-The tendency of a moving object to move along a straight line with constant velocity is called the Interia of motion.

Example- When a moving car stops suddenly, the passenger of the car leans forward. This happens for speed. As the vehicle is in motion, the entire body of the rider is in motion with the vehicle. As the vehicle comes to a stop, the passenger’s lower body comes to rest, but the upper body still leans forward to maintain momentum. The body wants to go As a result the passenger leans forward.

Newton’s first law of Motion: Definition of force

According to Newton’s first law of motion, a stationary object will always remain at rest and an object in motion will always move in a straight line with constant momentum unless forced to change state by an externally applied force. That is, what is applied from outside to change or try to change the static or dynamic state of an object is called force.

Or, a physical cause that changes or attempts to change the state of motion or the state of the rest of an object, known as force.

Newton’s first law of motion: Newton’s first law of motion, often known as the law of inertia, asserts that unless acted upon by an unbalanced force, an object at rest will remain at rest and an object in motion will continue travelling at a constant pace. This signifies that objects are resistant to changes in their state of motion. For example, if you are seated in a car that has come to a complete stop at a red light, the automobile will remain stationary until the light turns green and the car begins to move. This is due to the fact that the net force applied to the automobile is zero. Once the car begins to move, it will continue to move at a steady speed unless the brakes are applied, which creates an imbalanced force that slows the car down. Newton’s first law of motion is a fundamental physics principle that is used to describe a wide range of phenomena, from the movement of objects on Earth to the direction of planets in space. It is also an important idea in engineering because it is utilised to design and create moving equipment and structures.

What is Newton’s first law of motion?

Newton’s first law of motion states that unless and until an external force occurs on a body, it remains at rest or in uniform motion in a straight line.
In simple terms, Newton’s first law of motion states that a body will not begin to move unless and until an external force acts on it. Once set in motion, it will not stop or change velocity unless and until another force acts on it. The first law of motion is frequently referred to as the law of inertia. The first law of motion is determined by two conditions:

• When an object is at rest, its velocity (v = 0) and acceleration (a = 0) are both zero. As a result, the object remains at rest.
• Objects in motion: When an object is in motion, velocity (v 0) is not equal to zero, but acceleration (a = 0) is. As a result, the object will continue to move at the same velocity and in the same direction.

Newton’s first law of Motion Example

Here are a few applications of Newton’s first law of motion:

• A bowling ball moving down the lane. Unless stopped by an obstruction, the bowling ball will continue to roll down the lane. This is due to the bowling ball’s net force being zero. The force of gravity pulls the bowling ball downward, but the force of the lane pushing back is equal and opposite.
• An automobile driving down a straight street. Unless the car is turned or stopped by the brakes, it will continue to proceed along the road at a constant speed. This is due to the fact that the net force applied to the automobile is zero. The engine’s force pushing the car forward is equal to and opposite to the friction force between the tyres and the road.
• A satellite in orbit around the Earth. Unless dragged out of orbit by another force, such as the gravity of another planet, a satellite will continue to orbit the Earth. This is due to the satellite’s net force being zero. The force of gravity between the Earth and the satellite pulls the satellite towards the Earth, whereas the force of velocity keeps the satellite in orbit.

Daily life examples of Newton’s first law of Motion

Here are some real-world applications of Newton’s first law of motion:

• When you’re in a car and it abruptly stops, you tend to keep driving forward. This is due to inertia in your body, which means it resists changes in its state of motion. When the car comes to a stop, the force that was keeping your body moving forward abruptly disappears, and your body continues to travel forward until it is stopped by the force of the seatbelt or the dashboard.
• When you ride a bike and spin the handlebars abruptly, the bike tends to continue travelling in a straight line. This is due to the bike’s inertia, which opposes changes in the direction of motion. When you turn the handlebars, you apply a force to the bike, but this force is insufficient to overcome the bike’s inertia, thus the bike moves in a straight line for a short time.
• When you hit the cue ball while playing pool, it will continue to move in the direction you struck it until it is stopped by another object. This is due to inertia in the cue ball, which opposes changes in its direction of travel. The force of the cue stick striking the cue ball is sufficient to overcome the inertia of the cue ball, and the cue ball begins to move in the direction that you struck it. However, because of the force of friction between the cue ball and the table, the cue ball will finally stop moving.

Newton’s first law of Motion in Hindi

न्यूटन का प्रथम गतिकी नियम (Newton’s First Law of Motion) गतिविज्ञान में एक महत्वपूर्ण सिद्धांत है। इसे अक्सर ‘संयमितता का नियम’ भी कहा जाता है। यह नियम कहता है कि कोई वस्तु शांति अवस्था में या स्थिरता में रहेगी जब तक उस पर कोई बाह्य बल कार्रवाई न करे। अर्थात, यदि कोई वस्तु विलम्ब से गतिशील हो रही है, तो उसे इसी गति और दिशा में आगे बढ़ने के लिए एक बाह्य बल की आवश्यकता होती है। उसके बिना, वस्तु अपनी संयमितता के कारण अपनी वर्तमान गति या स्थिति को बनाए रखेगी।

इस नियम की महत्वपूर्ण विशेषता है कि यह वस्तुओं के लिए अभिकर्ष के नियम की पूर्णता रूप में निर्देशित रूप है। अर्थात, जब तक कोई बाह्य बल वस्तु पर प्रयोग नहीं करता है, तब वस्तु अपनी मूल स्थिति या गति को बनाए रखेगी। यह नियम भी सुरंगों, गोली, वाहनों, विमानों, इंजनों, गतिशील वस्तुओं आदि के डिजाइन में महत्वपूर्ण भूमिका निभाता है।

न्यूटन के प्रथम गतिकी नियम द्वारा स्पष्ट किया जाता है कि एक वस्तु यदि विलम्ब से गतिशील हो रही है तो उसे इसी गति और दिशा में आगे बढ़ने के लिए कोई बाह्य बल की आवश्यकता होती है, जो उसे प्रेरित करेगा। इस नियम की समझ बढ़िया होने से हम गतिशील वस्तुओं की चाल, गति, रोक-चाल, संवेग आदि को समझ सकते हैं।

Newton’s Second Law of Motion

The rate of change of momentum of an object is proportional to the force applied to the object and the change of momentum also occurs in the direction in which the applied force acts.

•Newton’s second law explains (i) the concept of momentum, (ii) the measure of force, (iii) the unit of force and (iv) the neutral principle of force.

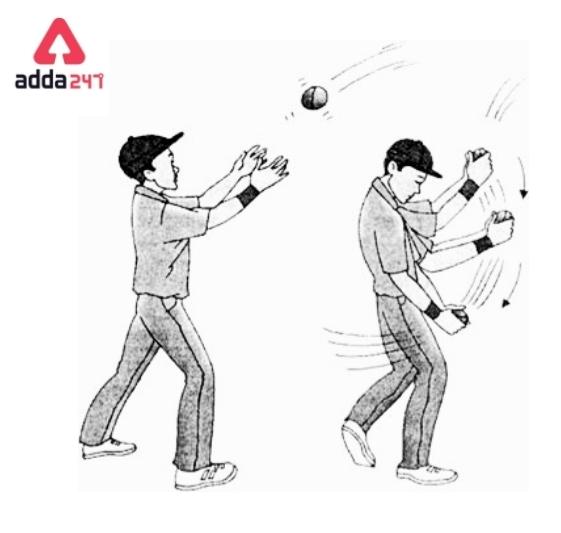
Newton’s second law of Motion: What is Momentum?

The amount of motion created by the combination of mass and velocity in a moving object is called the momentum of the object. The value of the momentum of an object is equal to the product of the object’s mass and velocity. If an object has mass m and velocity then the momentum of the object = m ×  v

Unit of Momentum- In C.G.S  Method The unit of momentum is – g. cm./s¹
In SI Method The unit of momentum is – Kg. m./s¹

Newton’s second law of Motion: Measurement of force

Let’s assume, an object having mass m, moving with a velocity of u. Force F is applied on the object for t time. Now, the formed acceleration in the object is a and the final velocity is v.

Initial momentum is = mu
After t time ,momentum is =mv
So, change in momentum = mv-mu [Final- Initial]

The Rate of changed  momentum = (mv-mu )/t
= m(v-u) /t = ma [ a= (v-u) /t ]
Acceleration of motion is derived by, Final velocity -Initial velocity /time

Newton’s second law states that the momentum change rate is proportional to the applied force on the object.  so,
F∝ ma
or, F = K×  ma, Here K is a constant. Its value depends on the unit of force. Now, if the force acting on an object of unit mass causes unit acceleration to be a unit force, i.e., when m = 1; If a = 1, then F = 1

1 = K .1.1
or, K = 1

Therefore, according to the above definition of unit force,
F = ma

i.e., applied force = mass of object x acceleration of the object.

Unit of force

Method	Unit
C.G.S,	Dyne
S.I,	Newton

Newton’s second law of motion: According to Newton’s second law of motion, an object’s acceleration is directly proportional to the net force exerted on it and inversely proportional to its mass. This means that the bigger an object’s net force, the greater its acceleration. The larger an object’s mass, the less acceleration it will experience for a given net force. If the object’s net force is zero, it will not accelerate and will remain at rest or in steady motion. This is one of physics’ most important principles, and it is used to explain a wide range of events, from the movement of objects on Earth to the direction of planets in space. When you push a shopping cart, for example, the force you exert on the cart is proportional to its acceleration. The cart will accelerate quicker if you push harder. When you leap, you are propelled into the air by the force of your legs pressing against the ground. The stronger your push, the higher you’ll jump. When a car stops, the force exerted by the brakes is proportional to the automobile’s deceleration. The faster the car slows, the harder you brake. Newton’s second law of motion is a fundamental physical law regulating objects’ movement. It is a handy tool for comprehending and predicting the behaviour of items in our environment.

What is Newton’s second law of motion?

Newton’s second law states that the acceleration of an object is determined by two variables: the net force acting on the object and its mass. The acceleration of the body is related to the net force applied to it and inversely proportional to its mass. This means that as the force acting on an object increases, so does the object’s acceleration. Similarly, as an object’s mass increases, the object’s acceleration decreases.

Newton’s second law is formally expressed as follows:

The acceleration of an item caused by a net force is directly proportional to its magnitude, in the same direction as the net force, and inversely proportional to its mass.
In equation form, this assertion is as follows:

Derivation of Newton’s Second Law of Motion

Newton’s Second Law of Motion states that the rate of change of momentum of an object is directly proportional to the net force applied to it and takes place in the direction of the applied force. The mathematical form of this law is expressed as F = ma, where F is the net force applied to an object, m is its mass, and a is the acceleration produced.

To derive Newton’s Second Law of Motion, let’s consider a body of mass m experiencing a net force F, which causes it to accelerate.

1. Assume that the object is initially at rest, so its initial velocity (u) is zero.
2. The body undergoes uniform acceleration (a) over a certain time period (t).
3. The final velocity of the object (v) can be determined using the equation of motion: v = u + at.

Now, we know that acceleration is defined as the rate of change of velocity. Therefore, we can rewrite the equation as:

a = (v – u) / t.

Substituting the value of v = u + at into the equation, we get:

a = (u + at – u) / t.

Simplifying, we have:

a = at / t.

Cancelling out the t terms, we obtain:

a = a.

This equation shows that the acceleration is equal to the acceleration itself, which is true.

Next, we introduce the concept of force into the equation. Newton’s First Law of Motion states that an object at rest or in motion will continue to remain in that state unless acted upon by an external force. In this case, the force applied to the object is responsible for its acceleration.

According to Newton’s First Law, the force required to produce the observed acceleration is directly proportional to the mass of the object. Mathematically, we can express this as:

F ∝ m.

Combining this proportionality with the previous equation, we can write:

F ∝ ma.

Introducing a constant of proportionality, we arrive at:

F = kma.

Here, k is the constant of proportionality. But we know that the constant of proportionality is equal to 1, which simplifies the equation to:

F = ma.

Thus, we have derived Newton’s Second Law of Motion, which states that the net force applied to an object is equal to the product of its mass and acceleration: F = ma.

Second Law of Motion formula

Assume a mass(m) travelling in a straight line with an initial velocity(u). The application of a constant force(F) throughout the time(t) uniformly accelerates it to velocity(v) in time(t).

The body’s initial and final momentum is,

p1 = mu

p2 = mv

Therefore, a Change in Momentum ∝ p2 – p1

∝ mv – mu

∝ m × (v – u)

Velocity is equal to displacement upon the time taken

Then, the rate of change of momentum ∝ m×( v − u )/t

The applied force will be, F ∝ m×(v- u)/t

F = k m(v-u)/t

F = k ma 

Here, a = (v-u)/t is the acceleration.

F = Net force applied

m = mass of the body

k = proportionality constant

For Changing Mass	For Constant Mass
Formulation of Force	F = m1v1 – m0v0 / (t1 – t0)	F = m(v1 – v0) / (t1 – t0)
Description	The net force acting on an object with changing mass.	The net force acting on an object with constant mass.

Application of Newton’s Second Law of Motion Class 9

Newton’s second law of motion has numerous applications in daily life. Here are a couple of such examples:

• Sports: Newton’s second rule of motion is applied in numerous sports to explain and improve athlete performance. In baseball, for example, the force of the bat hitting the ball is proportional to the ball’s acceleration, therefore a harder hit results in a quicker ball. The force of the quarterback’s throw in football is proportional to the acceleration of the ball, hence a stronger throw results in a longer pass.
• Many machines and buildings are designed and built using Newton’s second law of motion. The force of the wind acting on a bridge, for example, is proportional to the bridge’s acceleration, hence the bridge must be designed to resist the force of the wind. The force of the brakes operating on the car in cars is proportional to the car’s deceleration, hence the brakes must be built to be able to stop the car rapidly.
• Transportation: Newton’s second rule of motion is utilised to better understand and improve vehicle performance. For example, the force exerted by an engine on a vehicle is proportional to its acceleration, so a more powerful engine will result in a quicker vehicle. The force of the air acting on the wings of an aeroplane is proportional to its lift, therefore a bigger wing area results in more lift.
• Space exploration: Newton’s second rule of motion is used to comprehend and control spaceship velocity. For example, the force exerted by rocket engines on a spacecraft is proportional to its acceleration, therefore stronger engines result in a quicker spaceship. Because the force of Earth’s gravity pressing on a satellite is proportional to its acceleration, the satellite must be in a stable orbit around the Earth.

Newton’s Second Law of Motion in Hindi

न्यूटन का द्वितीय गतिकी नियम (Newton’s Second Law of Motion) गतिविज्ञान में एक महत्वपूर्ण सिद्धांत है। यह नियम कहता है कि किसी वस्तु की प्रवृत्ति (मोमेंटम) का रेट उस पर लगाए गए नेट बल के समानुपातिक होता है और यह बल उसके परिणामस्वरूप उत्पन्न होने वाली त्वरण की दिशा में होता है। इसका गणितीय रूप दिया जाता है: F = ma, जहां F वस्तु पर लगाए गए नेट बल को दर्शाता है, m वस्तु की मास है, और a वस्तु द्वारा प्राप्त त्वरण है।

इस नियम के अनुसार, जब एक वस्तु पर बाह्य बल प्रयोग किया जाता है, तो उस वस्तु पर प्रवृत्ति की दिशा में एक त्वरण प्राप्त होता है जो बल की आकारणीयता (मास) के समानुपातिक होता है। यदि एक वस्तु की मास बदलती है, तो उसकी प्रवृत्ति पर पड़ने वाले बल को परिणामस्वरूप त्वरण के साथ गणना किया जाना चाहिए।

इस नियम का उपयोग व्यापार, खेल, मोटरगाड़ी आदि में अपनाया जाता है। इसका अध्ययन हमें यह समझने में मदद करता है कि वस्तु को किसी निश्चित तरीके से गतिशील करने के लिए कितना बल लगाना चाहिए। इसके अलावा, यह नियम वैज्ञानिक अध्ययन में एक मूल तत्व है और इसे समझना महत्वपूर्ण है जब हम गतिविज्ञान की अध्ययन करते हैं।

Newton’s Second Law Class 9 Examples

Question: A car of mass 1200 kg is traveling with an initial velocity of 20 m/s. A constant force of 5000 N is applied to the car for a duration of 10 seconds. Determine the final velocity of the car.

Solution: Given: Mass of the car (m) = 1200 kg Initial velocity (u) = 20 m/s Force applied (F) = 5000 N Time duration (t) = 10 s

Using Newton’s Second Law of Motion: F = ma

We need to find the final velocity (v) of the car. Rearranging the formula, we have: F = ma => a = F/m

We know that acceleration (a) is the rate of change of velocity, so we can express it as a = (v – u)/t

Substituting the value of a, we get: (v – u)/t = F/m

Rearranging the equation to solve for v: v – u = (F/m) * t v = u + (F/m) * t

Substituting the given values: v = 20 + (5000/1200) * 10 v = 20 + (4.1667) * 10 v = 20 + 41.6667 v = 61.6667 m/s

Therefore, the final velocity of the car is approximately 61.67 m/s.

Question: A crate of mass 50 kg is being pushed across a horizontal floor with a constant force of 400 N. If the coefficient of kinetic friction between the crate and the floor is 0.3, calculate the acceleration of the crate.

Solution: Given: Mass of the crate (m) = 50 kg Force applied (F) = 400 N Coefficient of kinetic friction (μ) = 0.3

To calculate the acceleration of the crate, we need to consider the net force acting on it. The net force is the difference between the applied force and the force of friction.

The force of friction can be calculated using: Frictional force (Ff) = μ * Normal force

The normal force (Fn) is equal to the weight of the crate, which can be calculated using: Weight (W) = m * g

where g is the acceleration due to gravity (approximately 9.8 m/s^2).

Substituting the values, we have: W = 50 * 9.8 W = 490 N

Now, calculating the frictional force: Ff = μ * Fn Ff = 0.3 * 490 Ff = 147 N

To find the net force (F_net), we subtract the frictional force from the applied force: F_net = F – Ff F_net = 400 – 147 F_net = 253 N

Using Newton’s Second Law of Motion: F_net = m * a

Substituting the values, we have: 253 = 50 * a

Solving for acceleration (a): a = 253 / 50 a = 5.06 m/s^2

Therefore, the acceleration of the crate is approximately 5.06 m/s^2.

Newton’s Third Law of Motion

Every action has an equal and opposite reaction.

Explanation – When one object applies a force on another object, the second object also applies an equal and opposite force on the first object. The force exerted by the first object on the second object is called action and the opposite force exerted by the second object on the first object is called reaction. [ According to Newton’s third law, two forces are equal and opposite]

Newton’s Third Law of Motion: Examples

1. When a gun is fired, the gun exerts force on the bullet. This force causes the bullet to accelerate forward. Bullets also exert an equal and opposite reaction force on the gun. As a result, the gun moves backwards. So the person who fires the gun feels shocked.

2. When a rider jumps from a boat to the shore, the boat moves backwards. When launching from the boat, the rider exerts a force on the boat. As a result, the boat moves backwards. Immediately the boat exerts an equal and opposite reaction force on the rider, causing the rider to reach the shore.

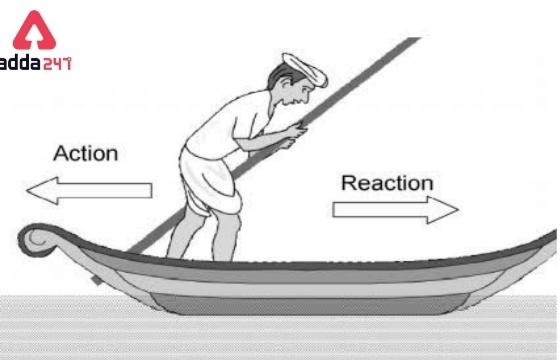
Newton’s third law of motion: According to Newton’s third law of motion, every action has an equal and opposite response. This means that when two things interact, they both exert forces on each other that are equal in magnitude and opposing in direction. When you jump, you are demonstrating Newton’s third law. When you push down on the earth with your feet, it pushes back up with equal force. This is what lifts you up into the air. Another example is when you discharge a firearm. When the gunpowder explodes, the bullet is propelled forward. The bullet then presses against the pistol, causing it to recoil. Newton’s third law is a fundamental physical law with several implications in our daily lives. It is responsible for the operation of rockets, the flight of aeroplanes, and our ability to walk and run.

Newton’s Third Law of Motion

Newton’s Third Law of Motion states, “There is an equal and opposite reaction to every action.” Newton’s third law distinguishes between two sorts of forces: action forces and reaction forces. These two forces have the same magnitude but act in different directions.

Newton’s third is so clear and lovely that it has become commonplace in our language. As a result, there are several misunderstandings. Here are some key points about Third’s law of motion:

1. The phrase’s action and reaction used in the third law indicate nothing else except ‘force’. Using several names to describe the same physical notion caused some misunderstanding. As a result, the forces occur in pairs and are applied in opposite directions.
2. The phrases action and reaction in Newton’s third law may give the erroneous impression that action precedes response, i.e. the action is the cause and reaction is the effect. However, there is no cause-and-effect relationship. As a result, the forces imparted are instantaneous. According to the same logic, one of them may be termed action and the other response.
3. Different bodies are affected by action and reaction forces, but not the same body. Summing up the two forces and asserting that the net force is zero is a mistake.

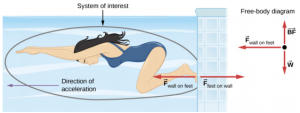
10 Examples of Newton’s third law of motion

Here are some examples of Newton’s third law of motion:

• Walking: When you walk, you push down on the ground with your feet. The ground pushes back up on you with an equal force, which propels you forward.
• Firing a gun: When you fire a gun, the gunpowder explodes, pushing the bullet forward. The bullet then pushes back on the gun, causing the gun to recoil.
• Swimming: When you swim, you push the water backward with your hands and feet. The water pushes back on you, propelling you forward.
• Riding a bike: When you ride a bike, you push the pedals down, which turns the wheels. The wheels push back on the ground, which propels the bike forward.
• Jumping on a trampoline: When you jump on a trampoline, you push down on the trampoline, which pushes back up on you, causing you to bounce up into the air.
• Taking off in a rocket: When a rocket takes off, the hot exhaust gases are expelled out the back of the rocket. The exhaust gases push back on the rocket, propelling it forward.
• Flying an airplane: When an airplane flies, the wings create lift. Lift is the force that pushes the airplane up into the air. Lift is created by the difference in air pressure between the top and bottom of the wings.
• Kicking a soccer ball: When you kick a soccer ball, you push the ball forward with your foot. The ball then pushes back on your foot, causing you to recoil backward.

These are just a few examples of Newton’s third law of motion. This law is a fundamental law of physics that has many applications in our everyday lives.

Examples of Interaction Force Pairs

Nature contains a wide range of action-reaction pairs. We have included a few examples below:

1. An action-reaction pair is the propulsion of a fish through water. A fish’s fins are used to push water backward. This push serves to propel the fish forward. The force on the water equals the force on the fish; the force on the water’s direction (backwards) is opposite the force on the fish’s direction (forwards).
2. The bird’s flight is an example of an action-reaction pair. The air is pushed downward by the bird’s wings. The air is pushed upwards by the air.
3. A swimmer pushes up against the water, and the water pushes back.
4. Helicopters generate lift by forcing the air downward, resulting in an upward reaction force.
5. Climbers use their vertical rope to propel themselves upwards.

Newton’s Third Law of Motion Formula

Whenever one body exerts a force on a second body, the first body experiences a force equal in magnitude and opposite in direction to the force it exerts. Mathematically, if a body A exerts a force⃗ on body B, then B simultaneously exerts a force – on A, or in vector equation form,

(A/B)=-⃗(A/B)

Newton’s Third Law of Motion in Hindi

न्यूटन का तृतीय गतिकी नियम (Newton’s Third Law of Motion) गतिविज्ञान में एक महत्वपूर्ण सिद्धांत है। यह नियम कहता है कि हर क्रिया प्रतिक्रिया के साथ आती है। इसका मतलब है कि जब एक वस्तु किसी अन्य वस्तु पर एक बल लगाती है, तो वही बल भी वस्तु को लगता है और उसे उत्तेजित करता है। इस प्रकार, दो वस्तुओं के बीच क्रिया और प्रतिक्रिया का संतुलन होता है।

इस नियम को आमतौर पर “एक समयी बलों का नियम” भी कहा जाता है। यह नियम स्पष्ट करता है कि जब दो वस्तुएं आपस में संपर्क करती हैं, तो उनमें प्रतिक्रियाशीलता होती है और एक दूसरे को एक समान और विपरीत बल लगाती हैं। इसलिए, एक बल एक वस्तु को प्रेरित करता है और उसी समय दूसरा वस्तु उसी मात्रा में प्रतिक्रिया द्वारा उत्तेजित होती है।

उदाहरण के तौर पर, यदि हम एक दीवार को मुक्त अवस्था से ठीक बांधे हुए गोल्फ गेंद पर एक मारते हैं, तो गोल्फ गेंद आगे की ओर आवारण ग्रहण करेगी, लेकिन साथ ही दीवार भी पिछड़ जाएगी। इस उदाहरण में, गोल्फ गेंद दीवार पर एक बल लगाती है और उत्तेजित होती है, जबकि दीवार भी गोल्फ गेंद के बल का समान और विपरीत बल उत्तेजित करती है और पिछड़ जाती है।

Newton’s Law of Motion Project PDF Class 9

Check here newton’s law of motion project pdf for class 9 Students. Check here now by Clicking on below link.

Newton’s Law of Motion Project PDF for Class 9 Students.

Related Post:

• Simple Microscope Diagram, Formula, Definition, Discovered By And Magnifying Power
• Laws Of Motion- First, Second, Third Law With Applications
• Fleming’s Left Thumb Rule Used For
• Cube Formula- Volume, Surface Area In Maths For Class 10
• Water Cycle Diagram For Kids Of Class 3 With Explanation
• 1 To 30 Square And Cube [ PDF Download ]
• Trigonometry Table (0 To 360): Formula, Value, Chart, Ratio, PDF For Class 10, 12

 

Sharing is caring!