Moment of Inertia Formula, Examples, Unit and Equations

The moment of inertia is a quantitative measure of the rotational inertia of a body—that is, the resistance that the body exhibits to having its speed of rotation along an axis altered by a torque. Learn about Moment of Inertia Definition, Formula, Examples, Unit and Equations

Table of Contents

The moment of inertia is a fundamental concept in rotational mechanics that measures an object’s resistance to angular acceleration around an axis. It plays a role analogous to mass in linear motion. Defined as the sum of the products of an object’s mass elements and the square of their distances from the axis of rotation, it depends on the shape, mass distribution, and orientation of the object. It determines how much torque is needed to achieve a desired angular velocity. Its applications span across engineering, physics, and everyday technologies, including wheels, gears, and flywheels.

Moment of Inertia Definition

The moment of inertia of a rigid body, also known as mass moment of inertia, angular mass, second moment of mass, or, more precisely, rotational inertia, is a quantity that determines the torque required for a desired angular acceleration about a rotational axis, in the same way, that mass determines the force required for a desired acceleration. It relies on the mass distribution of the body and the axis chosen, with higher moments necessitating more torque to affect the rate of rotation.

It is an extended property, the moment of inertia for a point mass is simply the mass times the square of the perpendicular distance to the rotation axis. In a rigid composite system’s it equals the sum of the moments of inertia of its component subsystems (all taken about the same axis). The second moment of mass with regard to distance from an axis is the simplest definition.

Torque must be supplied to a body that is free to rotate around an axis in order to modify its angular momentum. It is proportional to the amount of torque required to induce any given angular acceleration (rate of change in angular velocity).

Moment of Inertia Unit

Inertia moments are measured in kilogram meter squared (kgm2) in SI units and pound-foot-second squared (lbffts2) in imperial and US units.

Moment of Inertia Formula

The product of the mass of the section and the square of the distance between the reference axis and the centroid of the section is the moment of inertia.
By pulling in their arms, spinning figure skaters can minimize their moment of inertia, allowing them to spin faster due to the conservation of angular momentum.
The ratio of a system’s net angular momentum L to its angular velocity ω around a major axis is also known as the moment of inertia I

I = L / ω

If a system’s angular momentum remains constant, the angular velocity must increase as the moment of inertia decreases. To spin faster, figure skaters pull in their outstretched arms, whereas divers curl their bodies into a tuck position during a dive.

In general, an effective radius k can be defined for an object of mass m that is dependent on a particular axis of rotation and has a value such that its moment of inertia around the axis equals

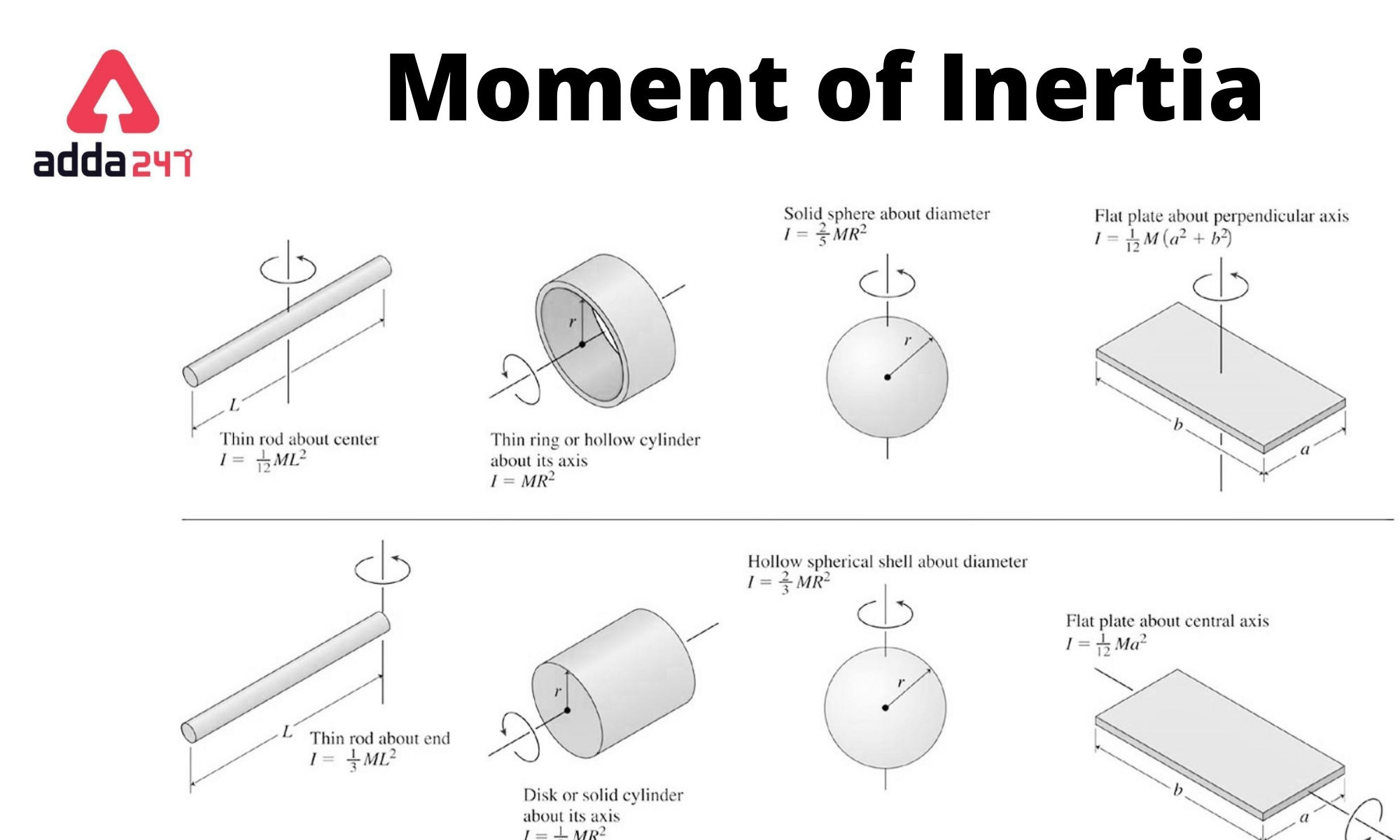
I=mk 2 The radius of gyration around the axis is known as k . Formula of Moment of Inertia The formula for the moment of inertia depends on the shape and distribution of the mass of the object. Here are the formulas for this phenomenon for some common shapes: In the following equations, I is represented as the moment of inertia Point Mass: For a point mass rotating about a fixed axis, the moment of inertia is given by: I = m * r^2 where m is the mass of the point mass, and r is the distance between the axis of rotation and the point mass. Thin Rod (Rotating about an End): For a thin rod rotating about an axis perpendicular to the rod and passing through one end, it is given by: I = (1/3) * m * L^2 where m is the mass of the rod, and L is the length of the rod. Thin Rod (Rotating about the Center): For a thin rod rotating about an axis perpendicular to the rod and passing through its center, it is given by: I = (1/12) * m * L^2 where m is the mass of the rod, and L is the length of the rod. Solid Cylinder (Rotating about Its Axis): For a solid cylinder rotating about an axis coinciding with its axis of symmetry, it is given by: I = (1/2) * m * R^2 where m is the mass of the cylinder, and R is the radius of the cylinder. Hollow Cylinder (Rotating about Its Axis): For a hollow cylinder rotating about an axis coinciding with its axis of symmetry, It is given by: I = m * R^2 where m is the mass of the cylinder, and R is the radius of the cylinder.

Moment of Inertia Factors

is an important concept in rotational dynamics and describes the object’s resistance to changes in its rotational motion. It is determined by the position of the motion’s axis of rotation, the distance between the various point masses from that axis of rotation, and the density of the material or item to be rotated along a fixed axis. The larger the mass points’ contribution to the system’s moment of inertia, the wider apart they are. You will have more inertia if you have more mass points. The following factors are as follows

i) The body’s mass.

ii) The body’s size and shape.

iii) Mass distribution around the axis of rotation

iv) The position and orientation of the rotation axis in relation to the body.

Examples of Moment of Inertia

Example 1: Simple Pendulum

The ratio of the torque due to gravity around the pivot of a pendulum to its angular acceleration about that pivot point is the moment of inertia of a simple pendulum. This is discovered to be the product of the particle’s mass m and the square of its distance r from the pivot for a basic pendulum, that is

I = m r ²

Example 2: FLYWHEEL of an automobile

A flywheel is a large mass situated on an engine’s crankshaft. The flywheel’s Moment Of Inertia is extremely large, which aids in energy storage.

Example 3: Hollow shaft

When opposed to a solid shaft, a hollow shaft transmits greater power (both of same mass). When compared to a solid shaft, the hollow shaft has a higher Moment Of Inertia.

Example 4: Shipbuilding

In shipbuilding, this quantitative measure has a significant impact. A ship can sink if it rolls, but it will never sink if it pitches.

Related Post:

FAQs

What is moment inertia?

The moment of inertia of an object is a computed measure for a rigid body rotating around a fixed axis: it measures how difficult it would be to modify the rotational speed of an object.

How to calculate moment of inertia?

Summing or integrating over each 'piece of mass' that makes up an object, multiplied by the square of the distance of each 'piece of mass' to the axis, yields moments of inertia.

What is difference between inertia and moment of inertia?

The resistance to angular acceleration is known as the moment of inertia (i.e. distribution of mass). Inertia is a linear mass attribute that describes how well an object resists a change in motion caused by a force, or how massive it is.

What is the moment of inertia for a disk?

The dimension of Mass Moments of Inertia is measured in (masslength2). It's important not to mix up the second moment of the area with the, which is utilised in beam calculations. The mass moment of inertia, also known as rotational inertia or angular mass, is a term used to describe the rotational inertia.

How do you explain inertia in very simple words?

The tendency of a body to resist a change in motion or rest is known as inertia. When you come to a complete stop in a vehicle, you tend to jerk forward. When the vehicle starts to move, you will jerk rearward in the same way.