Square Root 1 to 30 and Cube Root 1 to 30 are very important for all students who are preparing for their board exams. Not only for the board 1 to 30 square and cube also very crucial for the various one day competive exams.
In mathematics, a square root of a number x is a number y such that y² = x. In other words, a square root of a number is a number time itself equals the original number. For example, 4 and −4 are square roots of 16 because 4² = 16 and (-4)² = 16. On the other hand the cube of a number is the result of multiplying the number by itself three times. For example, the cube of 2 is 2 × 2 × 2 = 8. In this article, we will provide a list of square and cube 1 to 30 integers as well as square root and cube root 1 to 30.
Square and Cube 1 to 30 and Their Roots
1-30 Square and Cube: The list of square and cube 1 to 30 should help students to find out the perfect squares and cubes of integers. By memorizing those values students can solve any kind of simplification, Mensuration problems, Quadric equations, etc very easily and quickly. This list will help students to solve time-consuming numerical problems very quickly in an efficient way.
Square
The square of any number is obtained by multiplying the number by itself. Mathematically, if ‘n’ is any number, then the square of ‘n’ is represented as n², which equals n × n. For example, the square of 5 is 5², which equals 25 (since 5 × 5 = 25). This operation is used in various mathematical contexts and applications, including algebra, geometry, and in calculating areas of squares. The concept of squaring is foundational in mathematics and has practical applications in fields like physics, engineering, and computer science.
Cube
The cube of a number is calculated by multiplying the number by itself twice. It’s represented as the number raised to the power of 3. The formula for finding the cube of a number
is:
For example, the cube of 4 is calculated as
. This means that if you multiply 4 by itself two more times, you get 64. Cubing a number gives you the volume of a cube with sides of length equal to that number.
Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical notation, the square root of a number “x” is represented as √x. For example:
- The square root of 9 is √9, which is equal to 3 because 3 * 3 = 9.
- The square root of 16 is √16, which is equal to 4 because 4 * 4 = 16.
- The square root of 25 is √25, which is equal to 5 because 5 * 5 = 25.
Square roots can be both positive and negative. For example, the square root of 9 is both 3 and -3, because both 3 * 3 and -3 * -3 equal 9. However, in most contexts, when people refer to the “square root,” they are typically referring to the positive square root.
Cube Root
In mathematics, the cube root of a number x is denoted as ∛x, and it is the number which, when multiplied by itself three times, gives x. For example, the cube root of 27 is 3, since 3 × 3 × 3 = 27. For manual calculation, especially for non-perfect cubes, methods such as estimation or using the long division-like method for cube roots can be employed. These methods involve a step-by-step process to approximate the cube root value. Additionally, for computational purposes, programming languages and software tools can also calculate cube roots.
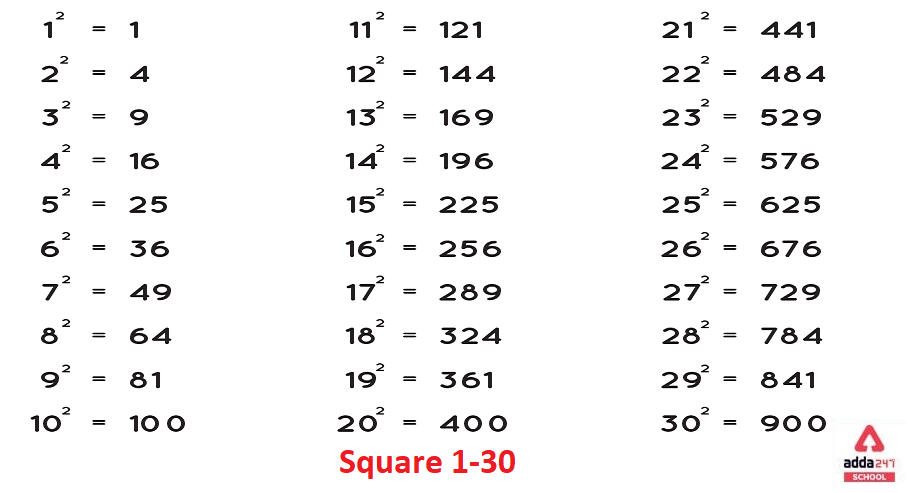
Square 1 to 30
Students can identify all perfect squares from 1 to 30 and approximate a square root by interpolating between known squares by learning squares 1 through 30. Here we give Square 1 to 30 in simple tabular form. Read all values and remember these values for future exams.
| Squares 1 to 30 | |
| 1² = 1 | 16² =256 |
| 2² = 4 | 17² =289 |
| 3² =9 | 18² =324 |
| 4²= 16 | 19² =361 |
| 5² =25 | 20² =400 |
| 6² =36 | 21² =441 |
| 7² =49 | 22² =484 |
| 8² =64 | 23² =529 |
| 9² =81 | 24² =576 |
| 10² =100 | 25² =625 |
| 11² =121 | 26² =676 |
| 12² =144 | 27² = 729 |
| 13² =169 | 28² = 784 |
| 14² =196 | 29² = 841 |
| 15² =225 | 30²= 900 |
Square Root 1 to 30
Square root 1 to 30 is given here in tabular form. The numbers 1, 4, 9, 16, and 25 are perfect squares in square roots 1 to 30, while the remaining numbers are non-perfect squares, i.e. their square root will be irrational.The square root can have both positive and negative values. Positive square root values from 1 to 30 range from 1 to 5.477.check all values for your board exams and for all other competitive exams.
| Square Root 1 to 30 | |
| √1 = 1 | √2 = 1.414 |
| √3 = 1.732 | √4 = 2 |
| √5 = 2.236 | √6 = 2.449 |
| √7 = 2.646 | √8 = 2.828 |
| √9 = 3 | √10 = 3.162 |
| √11 = 3.317 | √12 = 3.464 |
| √13 = 3.606 | √14 = 3.742 |
| √15 = 3.873 | √16 = 4 |
| √17 = 4.123 | √18 = 4.243 |
| √19 = 4.359 | √20 = 4.472 |
| √21 = 4.583 | √22 = 4.690 |
| √23 = 4.796 | √24 = 4.899 |
| √25 = 5 | √26 = 5.099 |
| √27 = 5.196 | √28 = 5.292 |
| √29 = 5.385 | √30 = 5.477 |
Cubes
The cube of a number is also known as the cubic power of the number.The cube of a number is found by multiplying it by itself three times. Cubes 1 to 30 are the cubes of the natural numbers 1 to 30 which are are particularly useful for solving many mathematical issues. Using the exponent’s formula, x³ yields the number’s cube. Assume we need to find a cube of 15.
15³= 15 × 15 × 15 = 225
Cube 1 to 30
When we multiply an integer itself three times, the value we get is the cube of that integer.
For example, 7 is an integer. Cube of 7 is =7×7×7= 343.
If ‘×’ is an integer, its cube is denoted by ‘ x³ ‘.
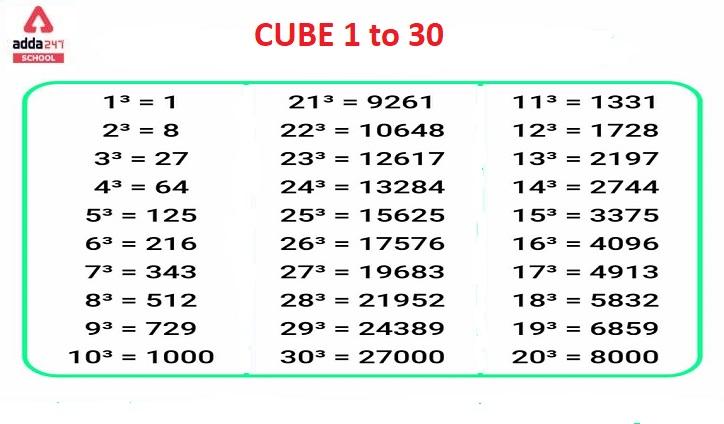
Cubes from 1 to 30 Table
Learning these cubes from 1 to 30 is really beneficial to students. Cube 1 to 30 is given in this table. read all values to solve cube-related problems quickly.Check out the values of Cubes 1 to 30 given in th below table.
| cubes from 1 to 30 (x³) | |
| 1³ = 1 | 16³ = 4096 |
| 2³ = 8 | 17³ = 4913 |
| 3³ = 27 | 18³ = 5832 |
| 4³ = 64 | 19³ = 6859 |
| 5³ = 125 | 20³ = 8000 |
| 6³ = 216 | 21³ = 9261 |
| 7³ = 343 | 22³ = 10648 |
| 8³ = 512 | 23³ = 12167 |
| 9³ = 729 | 24³ = 13284 |
| 10³ = 1000 | 25³ = 15625 |
| 11³ = 1331 | 26³ = 17576 |
| 12³ = 1728 | 27³ = 19683 |
| 13³ = 2197 | 28³ = 21952 |
| 14³ = 2744 | 29³ = 24389 |
| 15³ = 3375 | 30³ = 27000 |
1 to 30 Cube Root
Cube root 1 to 30 all values are given here in the below table. check all values and remember all of them for exams.
| Number | Cube Root (3√) |
| 1 | 1.000 |
| 2 | 1.260 |
| 3 | 1.442 |
| 4 | 1.587 |
| 5 | 1.710 |
| 6 | 1.817 |
| 7 | 1.913 |
| 8 | 2.000 |
| 9 | 2.080 |
| 10 | 2.154 |
| 11 | 2.224 |
| 12 | 2.289 |
| 13 | 2.351 |
| 14 | 2.410 |
| 15 | 2.466 |
| 16 | 2.520 |
| 17 | 2.571 |
| 18 | 2.621 |
| 19 | 2.668 |
| 20 | 2.714 |
| 21 | 2.759 |
| 22 | 2.802 |
| 23 | 2.844 |
| 24 | 2.884 |
| 25 | 2.924 |
| 26 | 2.962 |
| 27 | 3.000 |
| 28 | 3.037 |
| 29 | 3.072 |
| 30 | 3.107 |
Square Root 1 to 30 and Cube Root 1 to 30 PDF
The list of Square & Cube 1 to 30 will help students not only to find the square or cube values but also to recognize the perfect square of a number. Get the pdf of the square and cube 1 to 30 chart here.
squares and cubes 1 to 30 PDF Download
Problems based on Square root and cube root 1 to 30
Sloving the problems based square and cube 1 to 30 is the best way to memeorize the square root and cube root 1 to 30 or vice-versa effciently. Check out the following sloved examples.
Example 1- Find the value of [ 4³+ 11³ + 5²]
Solution- We know the values of 4³, 11³, and 5².
So, 4³+ 11³ + 5²
= 64+1331+ 25 = 1420 (Answer)
Example 2 – Calculate,[(28² – 9³) + 10² ]
Solution- [(28² – 9³) + 10² ]
= 784- 729 +100= 55 (Answer)
Example 3 – The length of one side of a cube is 6 cm. Calculate the volume of the cube?
Solution-The formula for determining the volume of a cube is – (side)³. The length of all sides of a cube is always equal.
So, the length of one side is 6 cm.
The volume of that cube is, V= 6³ cm³ = 216 cm³ (Answer)
Example 4 – Determine the total surface area of a sphere which have a radius of 3 cm.
Solution– The formula for determining the volume of the sphere is- A = 4π r² square units.
Total surface area – V= 4π( 3) ² cm²
A = 36 π cm² (Answer)
Example 5- The diameter of a circle is 14 cm. What is the area of the circle?
Solution-The formula for the area of a circle is, A= π r² square units.
The diameter of the given circle is – 14 cm.
So, radius of the circle is =14/2 = 7cm.
Area = π r²
Area= 22/7 ×(7²) [ here r = 7cm]
Area = 154 cm² .(Answer)
1 to 30 Square & Cube: Exercise
1. Find the value of [ 7³+ 13² + 21²]
2. Determine the circumference of a circle that has a radius of 21 cm.
3. Calculate the Area and Circumference of a square whose side length is 8 cm
4. If n² = 729, then n =?
5. The height of a cylinder is10 cm and the radius of one circular base is 7 cm. Find its volume.
Related post:
Greater Than and Less Than, Equal to Sig...
XXV Number- XXV Roman Numerals Definitio...
Ordinal Numbers: Meaning, Examples, Appl...
