Trigonometry Table- Learn Sin Cos Tan Table, Trigonometric Ratio Value Chart

A trigonometry table is a tool used in mathematics to provide values of trigonometric functions for various angles. Basically the basic trigonometric table includes values of standard angles like 30°, 45°, 60°, etc. Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles.

Trigonometric functions, such as sine (sin), cosine (cos), tangent (tan), cosecant (cosec), secant (sec), and cotangent (cot), are fundamental in solving various problems involving angles and distances. Trigonometric tables are very important for board exams and other competition exams as well.

Trigonometry Table

A trigonometry table typically lists these trigonometric functions for a range of commonly used angles, usually in degrees or radians. The angles are often given in increments of a few degrees or radians, making it convenient to quickly look up the corresponding values of the trigonometric functions without having to perform calculations manually.

In other words, A trigonometric table is used to find the values of trigonometric functions like sine (sin), cosine (cos), and tangent (tan) for common angles in degrees or radians. Here’s a basic trigonometry table for angles 0°, 30°, 45°, 60°, and 90°:

Angle (Degrees)	0°	30°	45°	60°	90°
Angle (Radians)	0	π/6	π/4	π/3	π/2
sin	0	1/2	√2/2	√3/2	1
cos	1	√3/2	√2/2	1/2	0
tan	0	1/√3	1	√3	Undefined

• Sine (sin) function gives the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
• Cosine (cos) function gives the ratio of the length of the adjacent side to the length of the hypotenuse.
• Tangent (tan) function gives the ratio of the length of the opposite side to the length of the adjacent side.

This table is fundamental in trigonometry, especially in solving problems related to right triangles and in various applications across physics, engineering, and mathematics.

Trigonometric Table

Modern trigonometric tables might also include values for hyperbolic trigonometric functions, which are analogs of the standard trigonometric functions but are based on hyperbolas rather than circles.

It’s important to note that with the prevalence of digital tools, trigonometric table functions can be easily calculated using calculators, computers, and various software applications. These tools can generate accurate and precise values for trigonometric Table functions for any angle, whether in degrees or radians.

Trigonometry Table Values

Trigonometry table showing the values of common trigonometric functions (sine, cosine, tangent, cosecant, secant, and cotangent) for angles in degrees:

Degrees (°)	Sine (sin)	Cosine (cos)	Tangent (tan)	Cosecant (csc)	Secant (sec)	Cotangent (cot)
0°	0	1	0	undefined	1	undefined
30°	1/2	√3/2	√3/3	2√3/3	2	√3
45°	√2/2	√2/2	1	√2	√2	1
60°	√3/2	1/2	√3	2/√3	2	1/√3
90°	1	0	undefined	1	undefined	0
120°	√3/2	-1/2	-√3	-2/√3	-2	-1/√3
135°	√2/2	-√2/2	-1	-√2	-√2	-1
150°	1/2	-√3/2	-√3/3	-2√3/3	-2	-√3
180°	0	-1	0	undefined	-1	undefined
210°	-1/2	-√3/2	√3/3	-2√3/3	-2	√3
225°	-√2/2	-√2/2	1	-√2	-√2	1
240°	-√3/2	-1/2	√3	-2/√3	-2	1/√3
270°	-1	0	undefined	-1	undefined	0
300°	-√3/2	1/2	-√3	2/√3	2	-1/√3
315°	-√2/2	√2/2	-1	√2	√2	-1
330°	-1/2	√3/2	-√3/3	2√3/3	2	√3
360°	0	1	0	undefined	1	undefined

Note: In this table, “undefined” indicates that the trigonometry formula is not defined for that particular angle. Also, the values shown are rounded to several decimal places for simplicity.

Trigonometry Sin Cos Table

Sin and Cos are two of the most fundamental trigonometric ratios and they are also the most widely used trigonometric ratios. It is because, using these trigonometric ratios, we can derive the reset of the trigonometric values, such as Tan, Cot, etc. So, learning the values of these ratios at standard angles like 0, 30, 45, 60, and so on becomes even more important.

The trigonometry table of Sin and Cos is very important to memorize for this reason. The Sin Cos trigonometric table, also known as the Sin Cos table is given below for standard angles from 0 to 360 degrees.

Sin Cos Table
Angles (In Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
Angles (In Radians)	0°	π/6	π/4	π/3	π/2	π	3π/2	2π
sin	0	1/2	1/√2	√3/2	1	0	-1	0
cos	1	√3/2	1/√2	1/2	0	-1	0	1

Trigonometry Table Class 10

Most Indian education boards introduce the concept of trigonometry to their students in class 10. Students who have just entered their final year of high school get haunted by realizing this fact. Trigonometry seems hard to students when they study it for the first time. This is so because trigonometry is a new concept for them.

For this purpose, the trigonometry table is designed for standard angles of 0, 30, 45, 60, and 90 degrees. This trigonometric table consists of the values of Sin and Cos for the above-mentioned standard angles. By memorizing this trigonometric table, one can easily ace their school examinations and lay a strong foundation for higher studies. The trigonometry table for class 10 is tabulated below.

Trigonometry Sin Cos Table Class 10
Angles	0°	30°	45°	60°	90°
sin	0	1/2	1/√2	√3/2	1
cos	1	√3/2	1/√2	1/2	0

Trigonometry Table Learning Tricks

It is very common for students to become nervous in the exam room. Due to this, their memory fades or they completely forget whatever they had memorized. In such scenarios, the trigonometry table trick comes into play. This trigonometric table learning trick will help you derive the values of all the trigonometric ratios. So, you no longer need to memorize the trigonometric table. By following the steps mentioned below, you will be able to find the values of trigonometric ratios for standard angles without memorizing the trigonometry tables.

Step 1: Write down the standard angles from 0 to 90 degree

Step 2: Start writing whole numbers starting from 0 below these standard angles, i.e., 0 for 0, 1 for 30 degree and so on

Step 3: Divide the whole numbers by the largest value, i.e., by 4

Step 4: Perform the square root operation on the divided result

Step 5: The final result are the corresponding values of Sin for those standard angles

Step 6: Write the values of Sin in reverse to get the corresponding values of Cos

With the values of sin and cos in hand, one can easily find the values for the rest of the trigonometric ratios. The aforementioned trick will help you derive the values of trigonometric ratios even if you somehow forget the trigonometric table.

Sin Cos Tan Table

The sine (sin), cosine (cos), and tangent (tan) are fundamental trigonometric functions. A table for these functions often includes values at key angles in degrees (and sometimes in radians) in a right-angled triangle. Here is a commonly used table for sin, cos, and tan at angles of 0°, 30°, 45°, 60°, and 90°:

Angle (°)	Sin	Cos	Tan
0	0	1	0
30	1/2	√3/2	1/√3
45	√2/2	√2/2	1
60	√3/2	1/2	√3
90	1	0	Undefined

These values are derived from the properties of right-angled triangles and the unit circle. They are fundamental in trigonometry and are widely used in various fields, including mathematics, engineering, and physics. It’s also important to note that the tangent function is undefined at 90° because it involves a division by zero (tan θ = sin θ / cos θ, and cos 90° = 0).

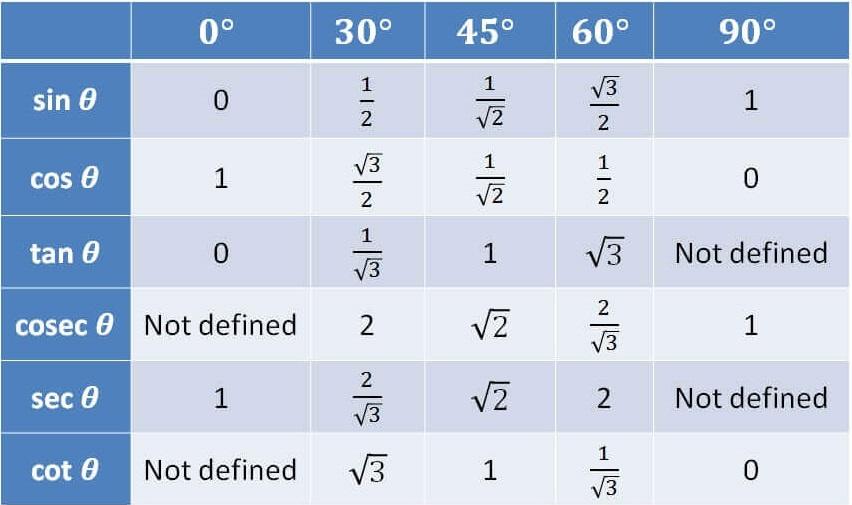
Trigonometric Ratio Table

Trigonometric ratios are included in the trigonometric table: sine, cosine, tangent, cosecant, secant, and cotangent. These ratios are abbreviated as sin, cos, tan, cosec, sec, and cot.  The Fast Fourier Transform algorithms are another notable application of trigonometric tables. In solving trigonometry issues, the values of trigonometric ratios of standard angles in a Trigonometry Table are useful. In this article, we will discuss the tricks to create the Trigonometric Table. Stay tuned and bookmark this page to get all the updates. 

Trigonometry Ratio Table

Trigonometry Ratio Table is given below in the table.

Trigonometry Ratio Table
Angles (In Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
Angles (In Radians)	0°	π/6	π/4	π/3	π/2	π	3π/2	2π
sin	0	1/2	1/√2	√3/2	1	0	-1	0
cos	1	√3/2	1/√2	1/2	0	-1	0	1
tan	0	1/√3	1	√3	∞	0	∞	0
cot	∞	√3	1	1/√3	0	∞	0	∞
cosec	∞	2	√2	2/√3	1	∞	-1	∞
sec	1	2/√3	√2	2	∞	-1	∞	1

Trigo Table

Students must know the Trigonometry relations between ratios because it makes it easy for students to learn the Trigonometry Table. Even trigonometric ratios are dependent upon trigonometric values. To ease the students below we have given the trigonometric table as well as the values. The students are advised to go through the trigonometry ratios and their relations first before jumping on the steps to learn trigonometric tables. If students will already know the trigonometric then learning trigonometry will be easy for them. 

Trigonometry Table 0-360 Value

Trigonometry Table (0-360) degree All values are given below.

1. sin x = cos (90° – x)
2. cot x = tan (90° – x)
3. sec x = cosec (90° – x)
4. cos x = sin (90° – x)
5. tan x = cot (90° – x)
6. cosec x = sec (90° – x)
7. 1/sin x = cosec x
8. 1/tan x = cot x
9. 1/cos x = sec x

Trigonometry Table Tricks To Learn Trigonometric Table

The Trigonometry Table is quite easy to remember for children of class 10 if you know all the trigonometry formulas. There is also a trick to learning trigonometric tables called the one-hand trick to memorize the trigonometric table.

Step 1: For the sine table, count the fingers on the left side for the standard angle.

Step 2: Divide the number of fingers on the left side (calculate in the 1st step) by 4

Step 3: Find the Square root of the value calculated in Step 2.

Learning the trigonometric table can be challenging, but several tricks and methods can help you memorize it more effectively. Here are some options:

(a) Use Mnemonics: Create a mnemonic device to remember the values. For example, for the sine values of 0°, 30°, 45°, 60°, and 90°, you could use the phrase “Some People Have Curly Brown Hair” to remember the sequence 0, 1/2, √2/2, √3/2, 1.

(b) Visualize the Unit Circle: Understand and visualize the unit circle, as it can help in remembering the sine and cosine values for common angles.

(c) Relate to Special Triangles: Memorize the properties of 30°-60°-90° and 45°-45°-90° triangles. These triangles reflect the sine, cosine, and tangent values for these angles.

(d) Practice Regularly: Regular practice through exercises and quizzes can help reinforce your memory of the trigonometric table.

The best option depends on your learning style and preference, but a combination of these methods can be very effective.

Solution:

• Mnemonics like “Some People Have Curly Brown Hair” are useful for quick recall.
• Visualizing the unit circle helps in understanding the trigonometric values as coordinates on a circle, providing a conceptual understanding.
• Relating to special triangles connects trigonometric values to geometric shapes, which can be easier to recall.
• Regular practice is essential for any learning and memorization process, as it reinforces the memory and aids in quick recall during exams or practical applications.

How to Create a Trigonometry Table?

We can easily create a Table by using the following steps-

Step 1: Make a table with the top row listing the angles such as 0°, 30°, 45°, 60°, 90°, and the first column containing the trigonometric functions such as sin, , cosec, cos, tan, cot, sec. 

Step 2: Calculating the value of sin for different angles: In ascending order, write the angles 0°, 30°, 45°, 60°, and 90° and assign them the numbers 0, 1, 2, 3, 4 according to the order. As a result, 0 will be assigned to 0°; 1 will be assigned to 30°; 2 will be assigned to 45°; 3 will be assigned to  60°; 4 will be assigned to 90°. Next, divide the values by four and square root the total value. 

 0° ⟶ √(0/4) = 0

30° ⟶ √(1 /4) = 1/2 

45° ⟶ √(2/4) = 1/ √2

60° ⟶√(3/4) = √3/2

90° ⟶ √(4/4) = 1

This offers the sine values for these 5 angles i.e. 0°, 30°, 45°, 60°, 90°. Now for the last three angles we will use the equation given below:

sin (180° − x) = sin x

sin (180° + x) = -sin x

sin (360° − x) = -sin x

Calculate the values of 180º, 270º, 360º   

sin (180° − 0º) = sin 0º 

Here we are taking x = 0 because we have to find the value of Sin 180º. Thus, putting x = 0º  is satisfying the equation.

sin (180° + 90º) = -sin 90º

Here we are taking x = 90º because we have to find the value of Sin 270º. Thus, putting x = 90º  is satisfying it.  

sin (360° − 0º) = -sin 0º

Here we are taking x = 0º because we have to find the value of Sin 360º. Thus, putting x = 0º  is satisfying the equation.

Angles (in Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
sin	0	1/2	1/√2	√3/2	1	0	-1	0

Step 3: To find the value of cos, we use sin (90° – x) = cos x. Use this it to calculate cos x for all the angles. 

Example: 

for value of X =  0°

Cos 0° = sin (90° – 0°) = sin 90°

for value of X =  30°

cos 30° = sin (90° – 30°) = sin 60°.

for value of X =  45°

Cos 45° = sin (90° – 45°) = sin 45°

for value of X =  60°

cos 60° = sin (90° – 60°) = sin 30°

for value of X =  90°

cos 90° = sin (90° – 90°) = sin 0°

for value of X =  180°

cos 180° = sin (90° – 180°) = -sin 90°

for value of X =  270°

cos 270° = sin (90° – 270°) = -sin 180°

for value of X =  360°

cos 360° = sin (90° – 360°) = -sin 270°

Angles (in Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
cos	1	√3/2	1/√2	1/2	0	-1	0	1

Step 4: Calculate the value of tan for all the angles.

 tan x = sin x/cos x

Calculate the value of tan by putting all the angles given above.

Angles (In Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
tan	0	1/√3	1	√3	∞	0	∞	0

Step 5: Calculate the value of the cot for all the angles. 

cot x = 1/tan x

Calculate the value of the cot by putting all the angles in the given above.

Angles (In Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
cot	∞	√3	1	1/√3	0	∞	0	∞

Step 6: Calculate the value of cosec for all the angles. 

cosec x = 1/sin x

Calculate the value of cosec by putting all the angles given above.

Angles (In Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
cosec	∞	2	√2	2/√3	1	∞	-1	∞

Step 7: Calculate the value of sec for all the angles. 

sec x = 1/cos x

Calculate the value of sec by putting all the angles given above.

Angles (In Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
sec	1	2/√3	√2	2	∞	-1	∞	1

Trigonometry Table 0 to 360 Degrees Values PDF

Trigonometry Ratios Table PDF

Sin Cos Tan Chart

The Trigonometry Table sin cos tan chart is given below. take a close look to remember.

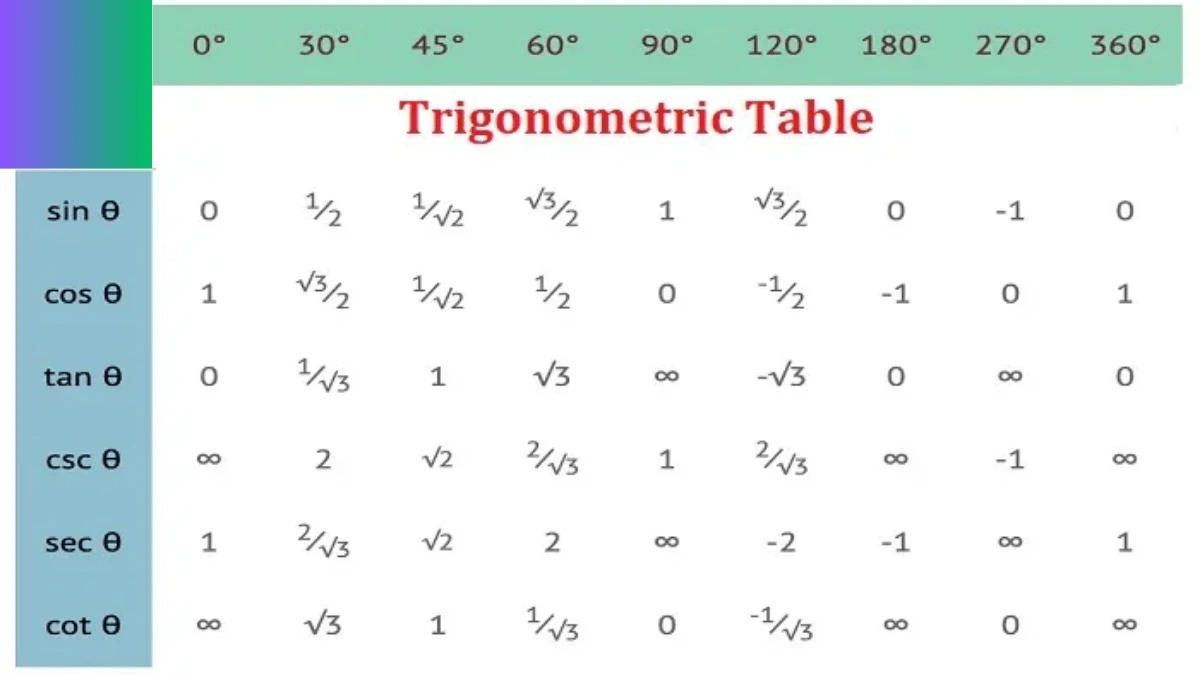
Trigonometry Table in Pi

Trigonometry Table in PI (π) check full table which is listed here.

Angles (In pi)	0°	π/6	π/4	π/3	π/2	π	3π/2	2π
sin	0	1/2	1/√2	√3/2	1	0	-1	0
cos	1	√3/2	1/√2	1/2	0	-1	0	1
tan	0	1/√3	1	√3	∞	0	∞	0
cot	∞	√3	1	1/√3	0	∞	0	∞
cosec	∞	2	√2	2/√3	1	∞	-1	∞
sec	1	2/√3	√2	2	∞	-1	∞	1

Trigonometric Table Examples

Q. Find the Exact value of Sin 15 using trigonometry table values.

Answer-  sin15 ° can be written as, sin(45° -30°)

sin15°= sin(45° -30°)= sin45° cos30°-cos45°sin30°,

[using sin(X-Y)=sinXcosY-cosXsinY] 

or,sin15° = (1/√2 ×√3/2)- (1/2×1/√2)  { using Trigonometry Table values }

sin15° = 1/√2 [(√3 -1)/2]

sin15° = (√3 -1)/2√2 (Answer)

Q. If θ =30°,prove that  cos 2θ =cos²θ -sin² θ

Answer- θ =30°

R.H.S –  cos²θ – sin² θ

= cos²30° – sin²30° = (1/2 )² – (√3/2 )² =3/4 – 1/4 = 1/2 

L.H.S – cos 2θ 

= cos 2 ( 30° )= Cos 60° = !/2 

Hence, L.H.S =R.H.S [ Proved]

Q. Find the length of the ladder which is leaning against a wall with an angle of 60° and the foot of the ladder is 12.4 m away from the wall.

Answer-  In the above question, the length of the base is 12.4 m. The elevation angle is 60°.

Now, let’s assume the length of the ladder is h m

Cos 60°= 12.4/ h

or,1/2 = 12.4/h

or, h = 2 ×12.4 = 24.8 m.

Hence, the length of the ladder is 24.8 m.

Trigonometry Table Practice Questions

1. Using Trigonometry Table, find the value of [4/3 tan²60° + 3cos²30° – 2 sec²30° – 3/4cot² 60°]

2. Proves that {sin²30° +cos²30° =1} , using Trigonometry  Table values.

3. Using Trigonometric Table, find the values of (a) tan (π/4)  (b) sec(π/6) ( c) sec(π/3

4. If the length of the shadow of a tree is √3 times its real height, then calculate the angle of elevation of the sun.

Sharing is caring!