Prime Numbers: Understanding the Basics and Importance
Students often encounter the question, “What are the prime numbers between 1 and 100?” In mathematics, there are several types of numbers such as even numbers, odd numbers, prime numbers, composite numbers, and more. Among these, prime numbers are particularly interesting and can sometimes confuse students.
But what exactly is a prime number? A prime number is a natural number greater than 1 that has only two distinct positive divisors: 1 and itself. In contrast, a composite number has more than two factors. For example, 2, 3, 5, 7, and 11 are prime numbers, while 4, 6, 8, and 9 are composite numbers.
In this article, we will explore the concept of prime numbers, how to identify them, and their significance in various fields of mathematics and beyond.
Prime Numbers
Prime numbers play an important role in the number system. These numbers are those that are bigger than 1 which simply have two factors: the number itself and factor 1. This indicates that these natural numbers cannot be divided without leaving a remainder by any number other than 1 and the number itself. The whole positive number system can be divided into two groups based on factorization: Prime numbers (with only 2 factors) and composite numbers.
What is Prime Number? Definition
The definition of Prime Number states that “every natural number bigger than 1 which has only two factors: 1 and the number itself. For instance, the number 5 is prime because there are only two ways to write it as a product, 1, 5 and 5, 1. But 4 is not a prime number since it has more than two factors: 1, 2 and 4. Prime numbers are infinitely abundant and form the building blocks of the entire number system.
Prime Numbers 1 to 100
There are 25 prime numbers between 1 to 100. Following is a list of prime number from 1 to 100.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
History of Prime Numbers
Since ancient times, the prime number has piqued people’s interest, and mathematicians are still looking for prime numbers with magical powers. The prime number theorem, proposed by Euclid, states that there are an unlimited no. of prime number.
Eratosthenes was a famous scientist who devised a clever method for calculating all prime number up to a certain quantity. The Eratosthenes Sieve is the name given to this procedure. We’ll build a list of all numbers from 2 to n if you need to locate prime numbers up to n. All multiples of 2 except 2 will be struck from the list starting with the smallest prime number, p = 2. Assign the next value of p, which is a prime number bigger than 2, in the same way.
Prime Number Examples
Some prime numbers are: 2, 11, 23, 29, 37, etc. Natural numbers which are greater than 1 that are divisible by 1, themselves and any other numbers are excluded from the prime number series. These numbers are also known as composite numbers. For example, 2, 3, 5, 7, and 11 are prime number, while 4, 6, 8, and 9 are composite numbers. A composite number is a natural number greater than one that is not prime.
Prime Numbers from 1 to 200
Prime numbers from 1 to 200 list are given below, which we can learn and crosscheck if there are any other factors for them.
| Prime Number from 1 to 200 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199 |
All Prime Numbers 1 to 1000
Prime Numbers 1 to 1000 are given in the below table. There are a total of 168 prime number between 1 to 1000. They are:
| Prime Numbers List 1 to 1000 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997. |
Prime Numbers Chart 1 to 100
The chart of prime numbers between 1 to 100 in each intervals of 10 is given hereunder.
| All Prime Numbers 1 to 100 Table | |
| Prime number from 1 and 10 | 2, 3, 5, 7 |
| Prime number from 10 and 20 | 11, 13, 17, 19 |
| Prime number between 20 and 30 | 23, 29 |
| Prime number between 30 and 40 | 31, 37 |
| Prime number between 40 and 50 | 41, 43, 47 |
| Prime number between 50 and 60 | 53, 59 |
| Prime number between 60 and 70 | 61, 67 |
| Prime number between 70 and 80 | 71, 73, 79 |
| Prime number between 80 and 90 | 83, 89 |
| Prime number between 90 and 100 | 97 |
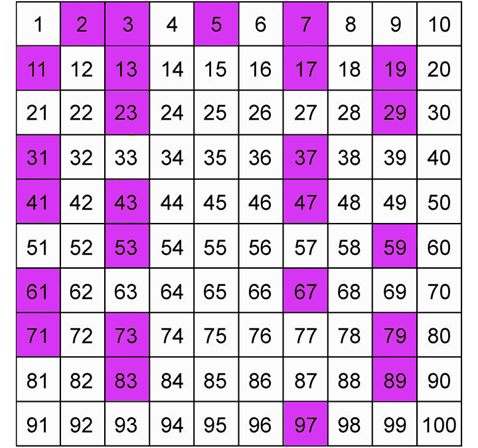
Properties of Prime Numbers
The following are some of the most essential qualities of prime numbers:
- It is made up of only two factors: 1 and the number itself.
- There is just one prime number that is even, which is 2.
- Any two prime numbers will always be co-prime to one another.
- A prime number is a whole number that is greater than or equal to one.
- The product of prime numbers can be used to express any integer.
How to Identify Prime Numbers
One of the easiest methods to find out prime number is the “Sieve of Eratosthenes”. Determining whether a given number is prime or composite can be achieved through various methods. One approach is to divide the number by all smaller numbers up to its square root.
If no divisors other than 1 and itself are found, the number is prime. However, this method becomes inefficient for larger numbers. Another popular technique is the Sieve of Eratosthenes, which involves iteratively eliminating multiples of prime numbers to identify prime numbers within a given range. There are a few tricks to find out prime number. Here are some of them:
- Factorization method: This is the most basic method of finding the prime number. You can factor a number into its prime factors. If a number has only two factors, 1 and itself, then it is a prime number.
- Sieve of Eratosthenes: This is a more efficient method of finding a prime number. It works by creating a list of all the numbers from 2 to a given number. Then, you start at the prime number 2 and cross out all the multiples of 2. Then, you move on to the next prime number, 3, and cross out all the multiples of 3 that are not already crossed out. You continue this process until you reach the square root of the given number. Any numbers that are not crossed out are prime numbers.
- Trial division method: This is the simplest method of finding prime numbers. You simply start at 2 and divide the given number by all the numbers from 2 to the square root of the given number. If the given number is divisible by any of these numbers, then it is not a prime number. If it is not divisible by any of these numbers, then it is a prime number.
Trick to Find Prime Numbers 1 to 100 Using Sieve of Eratosthenes
To find prime numbers, we apply a method called “Sieve of Eratosthenes” that can easily filter out prime number from composite numbers. Let us learn the steps of finding prime numbers between 1 to 100.
| Trick to Find Prime Number 1 to 100 using Sieve of Eratosthenes | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
- Make a table format like shown above.
- Now leave the number 1 as it is because all prime numbers are greater than 1.
- Highlight the number 2 as it is a prime number but leave all the multiples of 2 as it is.
- Next, number 3 and 5 are also prime number; highlight them but leave all of their multiples as it is.
- Lastly, the number 7 is left, keep all the multiple of 7 as it is and finally leftover numbers are prime number as highlighted in the above table.
Prime Number Significance
The prime number plays a crucial role in numerous fields, including cryptography, number theory, and computer science. They form the foundation of encryption algorithms used to secure sensitive information in modern communication systems.
Additionally, prime numbers are fundamental in the study of patterns, distribution, and factorization of numbers. They have practical applications in areas such as prime factorization, which is vital for data encryption and decryption.
Prime Numbers Uses
Prime numbers, with their unique properties and applications, continue to captivate mathematicians and researchers alike. From their role in cryptography to their significance in number theory, prime number serves as an essential cornerstone in various domains. Embracing the beauty and intrigue of prime number can deepen our understanding of the fascinating world of mathematics.
How many Prime Numbers between 1 and 100?
There are 25 prime numbers between 1 and 100. These are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 73, 79, 83, 89, and 97. Only 1 and the number itself divide each of these numbers. These numbers are hence referred to be prime numbers. These are the first 25 prime number, as well.
Difference Between Prime Numbers and Composite Numbers
A prime number is a number over 1 with only two factors, while a composite number has more than two factors. One way to factorize the number 5 is by multiplying 1 and 5, or by multiplying 5 and 1. It has just a pair of factors, specifically 1 and 5. Hence, 5 is a prime numeral.
A composite number is a number that is bigger than 1 and has more than two factors. For instance, 4 can be decomposed in various ways. Therefore, the divisors of 4 are 1, 2, and 4. It possesses more than two multiples. Hence, 4 is a non-prime number.
Let’s grasp the distinction between prime numbers and composite numbers using the provided table.
| Prime Numbers | Composite Numbers |
| These are numbers, greater than 1, having only two factors, 1 and the number itself | These are numbers greater than 1 having at least three factors |
| 2 is the smallest and the only even prime number | 4 is the smallest composite number |
| Examples of prime numbers are 2, 3, 5, 7, 11, 13, and so on. | Examples of composite numbers are 4, 6, 8, 9, 10, and so on. |
Difference Between Prime and Coprime Numbers
Prime numbers and co-prime numbers are not the same. The distinctions between prime numbers and co-prime numbers are outlined below.
Co-prime numbers are always viewed as pairs, whereas a prime number is an individual number.
Numbers are considered co-prime if they do not share any factors except for 1. There is no condition for prime numbers.
Co-prime numbers can be either prime or composite, as long as they have a Greatest Common Factor (GCF) of 1. Prime numbers are distinguished from composite numbers by having only two factors, which are 1 and the number itself. You can study about the coprime numbers in detail by clicking the following link.
Know about Coprime Numbers Here
Is 1 a Prime Number?
No. We can’t categorize the 1(one) in the prime numbers 1 to 100 List. A number can only be called a prime number if it has two positive elements. Now, the number of positive divisors or factors for 1 is simply one, which is 1. As a result, one is not a prime number.
What is the Smallest Prime Number?
The smallest prime number is 2. It’s also the only even prime number; all other even numbers, at least 1 and 2, maybe divided by themselves, implying that they’ll have at least three factors.
Largest Prime Numbers
The largest prime number cannot be identified since numbers are limitless and the highest prime number cannot be defined. The largest prime number will be found at infinity, so it cannot be defined.
Odd Prime Numbers
It is important to mention that, with the exception of 2, all prime numbers are odd numbers. It is interesting to note that 2 is the only even prime number. This implies that the odd number sequence can begin at 3 and go on, as the remaining prime number are also odd. Odd prime numbers include 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and more.
Even Prime Numbers
The sole even prime number is 2. This implies that every even number is a composite number. 2 qualifies as a prime number due to its sole factors being 1 and the number 2 itself.
What are Twin Prime Numbers?
Twin prime numbers or twin primes are prime numbers that have only one composite number between them. Another way to define twin prime numbers is as a pair of prime numbers that are only 2 numbers apart. 3 and 5 are twin primes as an illustration, with a difference of 2 when subtracted. Other instances of twin prime numbers include:
- (5, 7) [7 – 5 = 2]
- (11, 13) [13 – 11 = 2]
- (17, 19) [19 – 17 = 2]
- (29, 31) [31 – 29 = 2]
- (41, 43) [43 – 41 = 2]
- (59, 61) [61 – 59 = 2]
- (71, 73) [73 – 71 = 2]
Prime Numbers Things to be Remember
Some Prime Numbers between 1 to 100 key points are given below.
- One and zero are not prime numbers, these are categorized as special or unique numbers.
- 2 is the only even prime number; the rest are odd.
- Divisible by one, and the number itself is a prime number.
- A prime number greater than five and ends with five can be divided by 5, so it cannot be a prime number.
Solved Examples of Prime Numbers 1 to 100
Some solved examples on the concept of prime number is given below.
Question 1: Identify the prime numbers from the following list?
17,36,55,79,97
Answer: As per the given list, 17, 79 and 97 are prime numbers. 36 and 55 are composite numbers.
Question 2: Why 25 is not a prime number?
Answer: 1, 5 and 25 are the factors of 25. And since 18 has more than two factors it is not considered a prime number.
Question 3: Find the next four numbers of the following series:
- 67,71, 73…..
- 4, 5, 7…
Answer:
1. It’s a prime number series:
79, 83, 89, and 97 are the next four numbers.
2. In this series each consecutive prime number is added by 2:
2+2=4
3+2=5
5+2=7
So the next four numbers will be 9, 13, 15 and 19.
Question 4: How many prime numbers are between 1 to 100?
Answer: There are 25 prime numbers between 1 to 100.
Question 5: Which of the given ten numbers are prime number; 1,3,10,33,56, 59, 71, 77,89,99 ?
Answer: 3, 59, 71 and 89 are prime numbers as these have only two factors – one and the number itself. We can verify this result from the list of prime number between 1 to 100 as shown above.
Practice Questions on Prime Numbers
Here we discussed some Prime Number sample practice questions.
Question 1: Find the average of the last ten prime number?
Question 2: Why is 1 not a prime number?
Question 3: Which is the largest two-digit prime number?
- 97
- 99
- 75
- 84
Question 4: Write the four pairs of prime number less than 20?
Question 5: Is 78 a prime number?
| Related Articles | |
| Even Numbers | Odd Numbers |
| Co-Prime Number | Integers |
| Ordinal Numbers | Roman Numbers |









 CUET UG Final Answer Key 2025 Revised, D...
CUET UG Final Answer Key 2025 Revised, D...
 DU Cut off 2025, Delhi University Expect...
DU Cut off 2025, Delhi University Expect...
 OUAT Result 2025 OUT @ouat.nic.in: Check...
OUAT Result 2025 OUT @ouat.nic.in: Check...









