In mathematics, integers are a collection of both positive and negative numbers. it does not include fractions. Thus, we can say, that integers are numbers that can be positive, negative, or zero, but cannot be a fraction. We can perform all arithmetic operations on integers, including addition, subtraction, multiplication, and division. Examples of such numbers are -60,-55,-5, -20,0,4. 8,19,15 etc. In this article, we are going to learn about Integers, their definition, Examples, types, and Properties, and solve some problems based on them.
Integer Definition
Integers are the primary unit of mathematics. The meaning of Integer is Intact or whole. Groupings of positive and negative numbers along with zero are known as integers. These sets of numbers do not contain fractions and decimals just like whole numbers. it can be positive, negative, or zero and can be used for all arithmetic operations, including addition, subtraction, multiplication, and division.
What is Integers?
Integers are the set of whole numbers that include all positive numbers (1, 2, 3, …), their negative counterparts (-1, -2, -3, …), and zero (0). In mathematical notation, the set of integers is often denoted by ℤ, which is derived from the German word “Zahlen,” meaning “numbers.”
Integers Numbers
In mathematics, Integers are a set of numbers that include all the whole numbers (both positive and negative) as well as zero. it is represented with ” Z”. In mathematical terms, the set of is often denoted by the symbol ℤ. This set includes:
Examples include of such numbers are -39,-20,-12- 5, 1, 8, 10,20 -12, and so on.
Also, it can be written as,
Z ={ ……-4,-3,-2,-1,0,1,2,3,4,……….}
- Positive integers:
(also called natural numbers)
- Negative integers:
- Zero:
Types of Integers
In maths, three types of Integers are there. Those are- Negative, Positive integers, and Zero. Let’s briefly know about them.
Negative Integers
Integers with a negative value are those that are less than zero. They exclude decimals and fractions.
Examples of negative integers are -40,-7,-8,5,-4, -3-2,-1
Z- {∞,…….-10,-9,-8,-7,-6,-5,-4,-3,-2,-1}
Positive Integers
Positive Numbers also known as Natural Numbers are a set of numbers from 1 to infinity. Natural numbers do not include 0, negative integers (-1, -35, etc.), fractions, or decimals. The positive numbers from 1 to 10 are 1, 2, 3, 5, 6, 7, 8, 9, and 10.
Z+ = {1,2,3,4,5,6,7,8,9,10…∞}
Zero
The value of Zero is Null. But these are the most vital numbers in all Integers. Zero is neither a part of Positive nor a part of Negative integers.
Although Zero belongs to the whole Number set .in mathematics whole number ser is represented by the symbol W, which is written as { 0, 1, 2, 3, …….}
W = {0,1,2,3,4,5,6,7,8,9,10…∞}
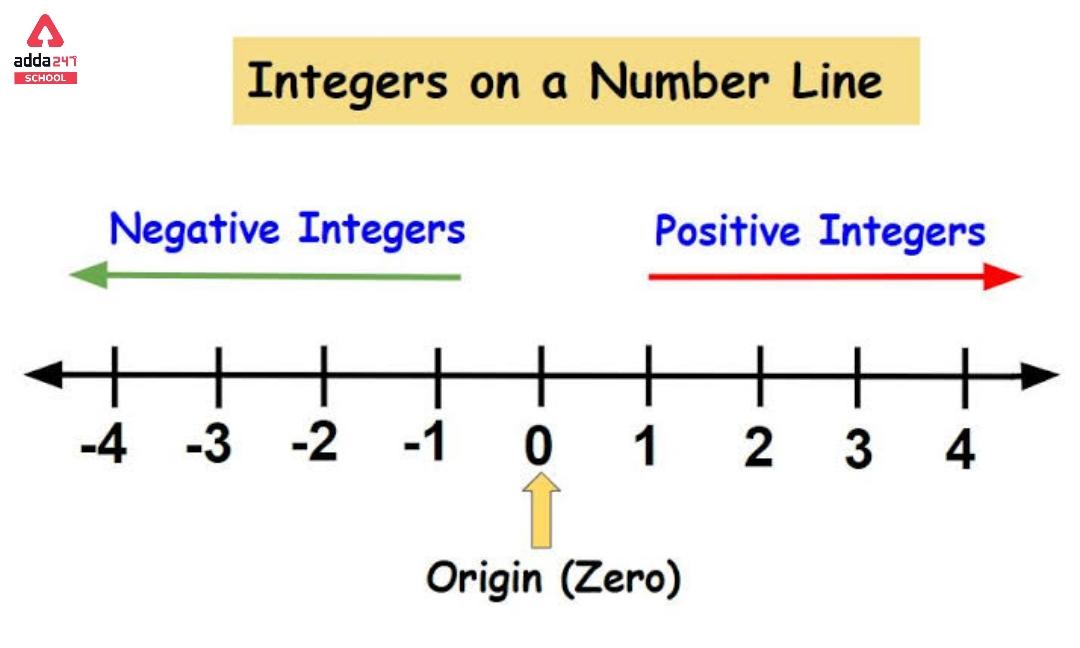
Integers on Number Line
A straight line of numbers is shown visually as a number line. As earlier we know, there are three types of integers -Zero, positive, and Negative integers. They can be simply represented on a number line.
• The center of an integer on a number line is zero. It cannot be positive or negative.
• On the number line, Positive integers are on the right side of zero
• Negative integers that are placed on the left side of the zero on the number line.
Integer Rules
For integers, the following rules are specified:
| Rules | Examples |
| The sum of two positive integers is always an integer. | (+ 5)+ (+40 )= + 45 |
| The sum of two negative integers, also be always an Integer. | (-8) +(-6) = -15 |
| An integer and its inverse have a total of zero. | 3+ (-3) =0 9 + (-9) = 0 |
| An integer’s product with its reciprocal is always one | [ 9 ×1/9 ] = 1 |
| If there is no sign in front of an integer then it is considered positive. | 20 denotes +20. |
| An integer has a positive absolute value | |5| =|+5| = 5. |
Arithmetic Operations on Integers
Integers can be used in the following four fundamental arithmetic operations:
1. Addition of Integers
2. Subtraction of integers
3. Multiplication of integers
4. Division of Integers
Let us understand the operations with examples.
1. Addition of Integers
The addition of two integers always results in an integer. But there is some rule while performing the Addition.
• while multiplying two absolute values of the two integers having the same sign, then write the sum of the integers using the sign indicated by the numbers.
• when two numbers having different signs added should be subtracted, and the difference should be expressed using the sign of the number with the highest absolute value.
For Example,
(+4) + (+7) = +11
(-6) + (-4) = -10
(-12)+ 3 = – 9
2. Subtraction of Integers
We follow the below guidelines while subtracting two integers:
•Change the subtrahend’s sign to make the operation become an additional problem.
•Then apply the same integer addition rules to solve the problem.
For example,
Substrate, 20 – 7
= 20 – (+7)
= + 13
Substrate , – 35 – 7
= -35 – (+7)
= – 42
3. Multiplication of Integers
The following guidelines are used when multiplying two integers:
| Operation | Results | Examples |
| (+) × (-) | – | 5× (-3) = -15 |
| (-) × (+) | – | (-5) × 3 = – 15 |
| (-) × (-) | + | (-5) × (-3) = 15 |
4. Division of Integers
While the division of two integers follows the guidelines,
| Operation | Results | Examples |
| (+) ÷ (+) | + | 21 ÷ 3 = 7 |
| (+) ÷ (-) | – | 21 ÷ (-3) = -7 |
| (-) ÷ (+) | – | (-21) ÷ 3 = – 7 |
| (-) ÷ (-) | + | (-21) ÷ (-3) = 7 |
Integers Numbers Properties
Major characteristics of integers include:
- Additive Inverse Property
- Multiplicative Inverse Property
- Closure Property
- Associative Property
- Commutative Property
- Distributive Property
Additive Inverse Property
A number’s opposite number is the additive inverse of that number. If 9 is an integer, its additive inverse is -9.
When an integer is multiplied by its additive inverse, the result is zero.
The simple rule is to flip from the positive to negative numbers or vice versa.
As The 9’s Additive integer is -9 then the sum of them is equal to 0.
[9+(-9]= 0
Multiplicative Inverse Property
The word Inverse means the opposite. Here Multiplicative Inverse means the reciprocal of an integer. Eg – Integer 4, its reciprocal is 1/4.
The Multiplicative Inverse Property of Integers suggests that if we multiply an integer with the reciprocal of that number the result is always One.
Integer 5, reciprocal 1/5
[ 5 ×1/5 ] = 1
Integer Closure Property
The Closure property of integers indicates that the set is closed for the given math operation. When two integers are added or multiplied, only an integer is produced.
For any two integers a and b:
a + b = integer
a – b = integer
a × b = integer
a/b = Integer
Integer Associative Property
Due to the associative Property of integers, when three or more numbers are added or multiplied, the resultant sum or product always comes out the same, regardless of how the numbers are arranged. Brackets are used to group the items in this sentence.
a × (b × c) = (a × b) × c
Commutative Property
According to the commutative property, If we move or swap the integers present in the operation then the solution will remain the same. No changes are there. But Subtraction and division are not affected by the property, which only applies to addition and multiplication.
Let’s suppose a and b are two integers.
a × b = b×a
a + b = b +a
Above both cases, the sum or the product will see although changes are made.
Distributive Property
When we distribute something, it means dividing that thing into equal parts. The distributive property of integers says that
Let three integers A, B and C then,
A ( B+ C) = A× B + A× C
Example: 8 x ( 4 + 6) = 8x 4 + 8x 6
LHS = 8 x (4+6 ) = 8 x 10= 80
RHS = 8 x 4 + 8 x 6 = 32+ 48 = 80
Hence, LHS = RHS (proved)
Integers Examples
Example 1. Prove, 10 ( 4 + 5) = 90
Solution- L.H.S- 10 ( 4 + 5)
= 10 x 9 =90= R.H.S ( Proved)
Example 2. Solve the following integer product:
- (+6) × (+12)
- (30) × (6)
- (- 9) × (6)
- 5 × (-4)
Solution:
- (+6) × (+10) = +50
- (30) × (6) = 1800
- (- 9) × (6) = -54
- 16 × (-5) = -80
Example 3. Solve the following Problems
- (-20) ÷ (4) = ?
- (-8) × (-4) = ?
- (169) ÷ (-13) = ?
Solution:
- (-20) ÷ (4) = -5
- (-8) × (-4)= 31
- (169) ÷ (- 13) = -13
| Other Formulas | |
| Simple Interest Formula | Trigonometry Formula |
| Algebra Formulas | Mensuration Formulas |









 Greater Than and Less Than, Equal to Sig...
Greater Than and Less Than, Equal to Sig...
 XXV Number- XXV Roman Numerals Definitio...
XXV Number- XXV Roman Numerals Definitio...
 Ordinal Numbers: Meaning, Examples, Appl...
Ordinal Numbers: Meaning, Examples, Appl...









