Does volume exist in 2D shapes?

No. Volume is the property of 3D shapes like cubes, cuboids, etc. 2D shapes can only have an area and perimeter.

Mensuration Formulas PDF for All 2D, 3D Shapes in Maths, Get Chart

Mensuration is a discipline of mathematics concerned with the measurement of geometric figures. Mensuration formulas are an important aspect of geometry and are utilized in a variety of mathematical and real-world contexts. It deals with dimensions such as shape, length, volume, area, surface area, and so on. Mensuration is the measurement of geometrical figures that fall into the categories of 2D and 3D shapes. Problems based on Mensuration Formula are very frequent in class 10 as well as in various competitive Exams. In this article, we have discussed all the mensuration all formulas for 2D and 3D Shapes in detail.

Mensuration Formula

Mensuration formulas are an important aspect of geometry and are utilized in a variety of mathematical and real-world contexts. In mathematics, Mensuration is the branch in which we learn about different measurements like length, area, volume, etc of different figures and shapes like cylinders, Sphere, etc. These formula aid in determining the size, shape, and volume of various things, and so play an important part in numerous industries such as engineering, architecture, and construction.

Mensuration Formulas for 2D and 3D Shapes

Mensuration is the discipline of geometry concerned with measuring area, length, and volume in 2D and 3D forms. Before we go into the mensuration all formulas, it’s important to understand the distinction between 2D and 3D figures. A 2D shape has only two dimensions, length, and breadth, whereas a 3D figure has three dimensions: length, breadth, and height. we measure for 2D shapes area (A) and perimeter (P). Volume(V), total, lateral, and curved surface area are all estimated in 3D.

2D Mensuration –A shape or figure that only has two dimensions i.e. length and width. This type of figure does not have any thickness and is a flat plane shape. In a 2D shape, we can only calculate the area and the perimeter of the 2d shape.

3D Mensuration – A shape or figure that has all three dimensions i.e length width and thickness, is known as a three-dimensional shape. In 3d shape, we can calculate volume, the area covered by a curved surface and the total surface area of the 3D shape.

Important Terms Used in Mensuration formulas

Lets, ‘s learn about some terminology that we are going to use in mensuration all formulas.

Area – Area defines as a quantity of surface that is surrounded by a shape. Abbreviation by ‘A’.

Volume – Volume is a quantity that expresses the amount of space covered by a three-dimensional shape. Abbreviation by ‘V’
Parameter – Parameter is a measurable factor by which we can measure the length of the boundary line of a closed figure. Abbreviation by ‘P’.
Curved Surface Area (CSA) – This is the total area of all curved surfaces.
Lateral Surface Area (LSA) – This is the whole area of the surface excluding the top and bottom.
Total Surface Area (TSA) – This is the total area of the object’s surfaces, including the bases.

Mensuration All Formulas

Now, you are clear about what is exactly? 2-D shapes and 3-D shapes, but still, for your better understanding, we will be given the mensuration formula tables for both the shapes below. Check out all formulas of mensuration for 2-D and 3-D shapes which are given below.

2D Mensuration All Formulas

In mensuration, some Important mensuration 2d formula for the area and perimeter of some 2D shapes are listed below-

Shape	Area ( Square units)	Perimeter (Units)
Square	a²	4a
Circle	π r²	2πr
Rectangle	l × b	2 ( l+ b )
Triangle	½ (b × h)	a + b + c
Right angle Triangle	½ (b × h)	b + hypotenus +h
Equilateral Triangle	√(3/4) × a²	3a
Rhombus	½ ×d1 ×d2	4 × side
Parallelogram	b × h	2 ( l+ b )
Trapezium	½ h(a+b)	a+b+c+d

3D Mensuration All Formulas Chart

some Important mensuration 2d formula for some 3D shapes are listed below-

Shape	Volume (Cubic units)	Curved or lateral surface area ( Square units)	Total surface area ( Square unit )
Cube	a³	4a²	6a²
Cone	(⅓) π r² h	π r l	Π r (r + l)
Cylinder	π r² h	2π r h	2πrh + 2πr²
Hemisphere	(⅔) π r³	2 π r²	3 π r²
Cuboid	l × b× h	2 h( l+ b )	2 ( lb+ bh+ hl )
Sphere	(4/3) π r³	4 π r²	4 π r²
Frustum of Cone	(1/3)Πh(R² + R. r + r²)	Π (R + r)l	π[(R + r)l+r²+R²]

Mensuration Formula for Class 8 and Class 10

Mensuration is one of the important concepts in class 8. Some of the formula for class 8 students is given below.

Area Formula

Area of Trapezium = height × (sum of parallel sides)/2
Area of Rhombus = (1/2) × d1 × d2; where d1 and d2 are the two diagonals of the rhombus
Area of Special Quadrilateral = (1/2) × d × (h1 + h2); where d is the diagonal, and h1 and h2 are the perpendiculars drawn on the diagonals from the vertices.
Surface area of Cuboid = 2(lb + bh + hl); where l, b and h represent the length, breadth and height of the cuboid.
Surface area of Cube = 6s²; where s represents the side of the cube.
Surface area of cylinder = 2Πr(r + h); where h represents the height and r represents the radius of the cylinder.
Area of an equilateral triangle = s²(√3/4), where s = side of the equilateral triangle
Area of a regular hexagon = (3 x √3 x a²)/2, where a = side of the regular hexagon

Volume Formula

Volume of Cuboid = l × b × h; where l, b and h represent the length, breadth and height of the cuboid.
Volume of Cube = s³; where s represents the side of the cube.
Volume of Cylinder = Πr²h; where h represents the height and r represents the radius of the cylinder.
Volume of a Hollow Cylinder = Π. h(R² – r²), where R = outer radius, r = inner radius
Volume of a normal square pyramid = (1/3) x h x s², where s = length of one of the sides of a square base and h is the height of the pyramid

Mensuration Formulas Examples

Mensuration formulas is useful for measuring shapes and figures. It works with both 2-D and 3-D geometrical shapes. mensuration all formulas may appear intricate and difficult to employ, particularly to younger students. We’ve gone through various Mensuration math formulas for 2-D and 3-D figures in depth below.

Formulas of Cuboid

List of Cuboid formula are given below. learn all these formulas to speed up your calculations.

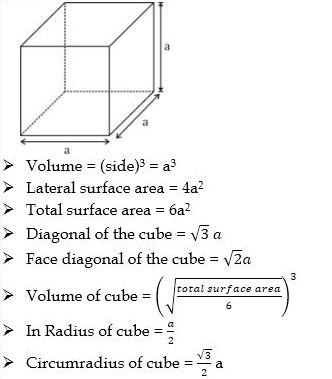
Formulas of Cube

Formula for Cube are given below.

Formulas of Sphere

Sphere Formula list is listed below.

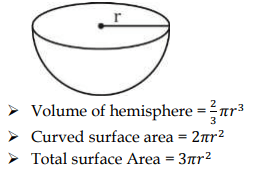
Formulas of Hemisphere

Check Formula for Hemisphere list is given below. Check now.

Formulas of Pyramids

Formula to solve Pyramids Problems are given below.

Formulas of Right Circular Cone

Right Circular cone formula is given below.

Mensuration Formulas PDF

We have provided the Mensuration Formulas PDF of some important formulas for 2D and 3D shapes below. These formulas will help students to prepare this topic for their school as well as competitive examinations.

Mensuration Formulas PDF

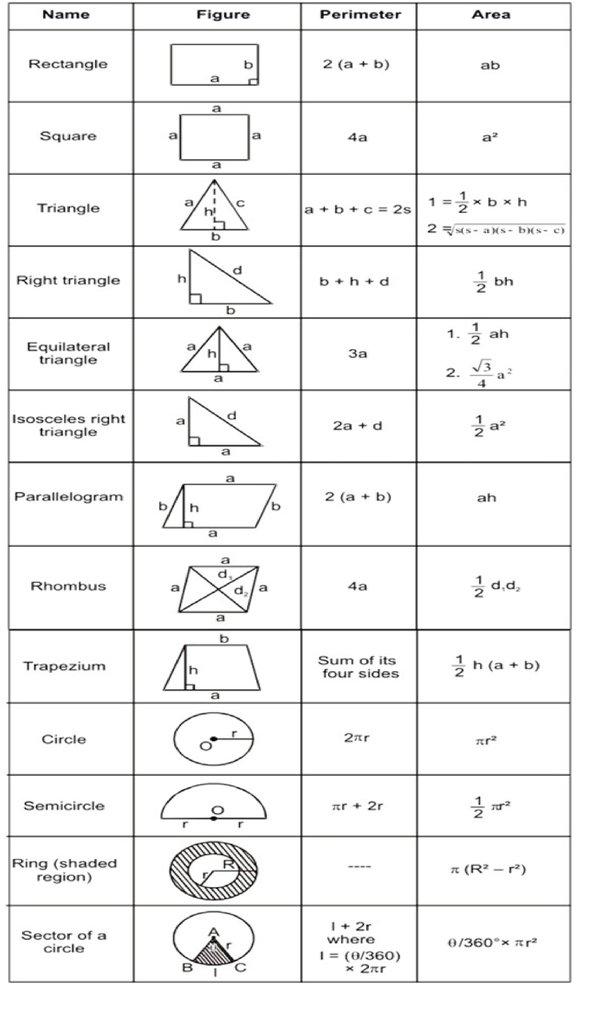
Mensuration Formula Chart

Check here the mensuration formula chart for students of Class 6 to 10.

Mensuration

“Mensuration” refers to the branch of mathematics that deals with the measurement of geometric figures and their properties. It involves the calculation of various measurements such as length, area, volume, and other geometric quantities. Mensuration is an important concept in geometry and has practical applications in fields such as architecture, engineering, construction, and design. Here are some common formula of mensuration for different geometric shapes:

2D Shapes:

Rectangle:
- Area: $A = length \times width$
- Perimeter: $P = 2 \times (length + width)$
Square:
- Area: $A = side^{2}$
- Perimeter: $P = 4 \times side$
Triangle:
- Area: $A = 2 1 \times base \times height$
- Perimeter: $P = side_{1} + side_{2} + side_{3}$
Circle:
- Area: $A = π \times radius^{2}$
- Circumference: $C = 2 π \times radius$

3D Shapes:

Cube:
- Volume: $V = side^{3}$
- Surface Area: $S A = 6 \times side^{2}$
Cylinder:
- Volume: $V = π \times radius^{2} \times height$
- Curved Surface Area: $CS A = 2 π \times radius \times height$
Sphere:
- Volume: $V = 3 4 π \times radius^{3}$
- Surface Area: $S A = 4 π \times radius^{2}$
Cone:
- Volume: $V =1/3 π \times radius^{2} \times height$
- Curved Surface Area: $CS A = π \times radius \times slant height$

These are just a few examples of mensuration formulas for various geometric shapes. Depending on the shape, different formulas are used to calculate measurements such as area, volume, and surface area. It’s important to understand the properties of each shape and how to apply the appropriate formula for the calculation of specific geometric quantities.

Shapes in Maths

In mathematics, shapes refer to the geometric figures or forms that can be defined by their size, dimensions, and properties. Geometry is the branch of mathematics that primarily deals with the study of shapes. Here are some fundamental shapes in mathematics:

Point: A point is a location in space with no size or dimension. It is often represented as a dot.

Line: A line is a straight path with no thickness or width. It extends infinitely in both directions.

Line Segment: A line segment is a portion of a line with two endpoints.

Ray: A ray is a portion of a line that starts at a particular point and extends infinitely in one direction.

Angle: An angle is formed when two rays share a common endpoint. Angles can be classified as acute (less than 90 degrees), right (exactly 90 degrees), obtuse (greater than 90 degrees but less than 180 degrees), or straight (exactly 180 degrees).

Triangle: A triangle is a polygon with three sides and three angles. The sum of the angles in a triangle is always 180 degrees.

Quadrilateral: A quadrilateral is a polygon with four sides and four angles. Examples include squares, rectangles, parallelograms, and trapezoids.

Circle: A circle is a two-dimensional shape with all points equidistant from its center. The distance from the center to any point on the circle is called the radius, and the distance across the circle passing through the center is the diameter.

Polygon: A polygon is a closed shape with straight sides. Polygons can have any number of sides, with common examples being triangles, quadrilaterals, pentagons, hexagons, etc.

Ellipse: An ellipse is a closed curve that resembles a flattened circle. It has two focal points, and the sum of the distances from any point on the ellipse to the two focal points remains constant.

Parabola: A parabola is a U-shaped curve that is symmetric about its vertex. It can open upward or downward.

Hyperbola: A hyperbola is a curve with two branches that are mirror images of each other. It has two focal points, and the difference in distances from any point on the hyperbola to the two focal points remains constant.

These are just some of the basic shapes in mathematics, and there are many more complex shapes and forms that mathematicians study and analyze. Shapes are fundamental to geometry and play a crucial role in various mathematical and scientific disciplines.

Solved Questions Based on Mensuration All Formulas

Q. If the area of a triangle with base ‘x’ is equal to the area of a square with side x .then the altitude of the triangle is :

a) x/2 b) x c) 2x d) 3x e) None of these

let, altitude of the triangle is – hIf base ‘x’, then the area of the triangle is – ½ (x × h) square unitsIf side ‘x’, then the area of the square is – square units

Now, as per the given condition,½ ( x × h) =x²or, h = 2x (Answer)

So, option ( c ) is correct.

Q . Find the area of a triangle whose sides are 5 , 5 & 6 cm .

a) 12 cm² b) b) 14 cm² c) 16 cm² d) 10 cm² e) None of these

So, area of the triangle = ½ (6 ×4 )

= 12cm² (Answer)

So, option ( a ) is correct .

Q . A cone and a hemisphere have equal bases and equal heights. Find out the ratio of their curved surface area .

a) 1: √2 b) √2 :1 c) 2 :1 d) 1:2 e) None of these

→Let the base radius of hemisphere = r unit .

Base radius of cone = r unit.

height of cone = base radius of hemisphere = r unit

so, Slant height of cone (l) =√(h²+r²)=√(r²+r²)=√2r unit

The ratio between the curved surface area of hemisphere and cone is –

= 2πr² : πrl = 2π²r: πr (√2r)=2 :√2= √2 : 1 ( Answer)

So, option ( b ) is correct.

Related Posts
Trigonometry Formula	Velocity Formula
Physics Formula	Algebra Formula
Integration Formula	Mensuration Formula
Time and Work Formula	Time and Distance Formula
Profit and Loss Formula	a3 b3 Formula