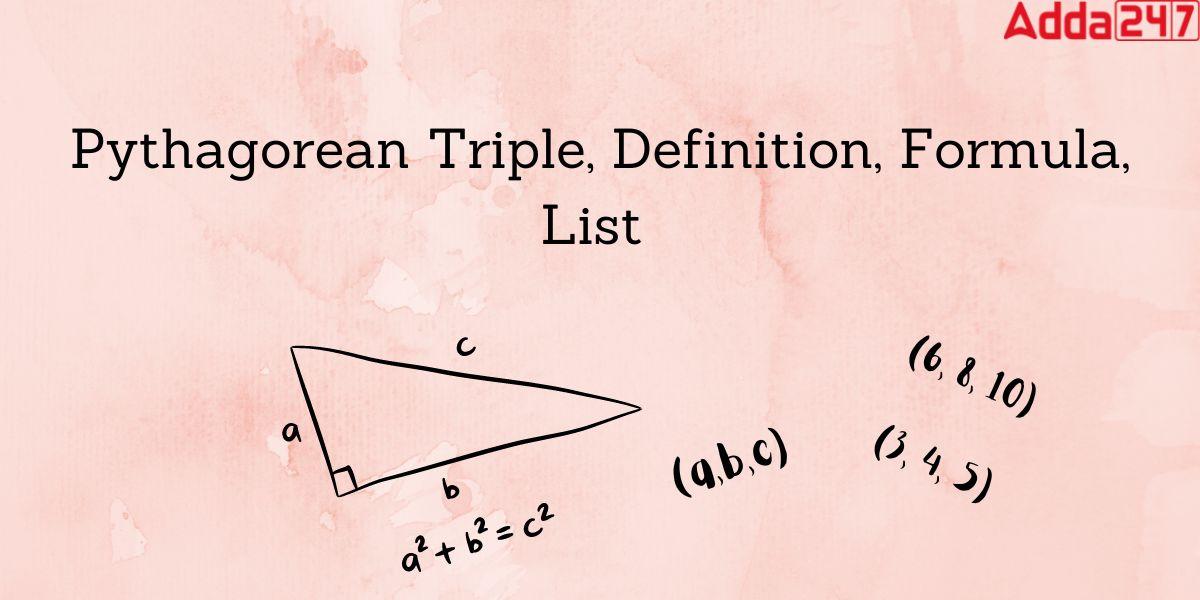
Pythagorean triples is a set of three positive integers which satisfy the Pythagorean theorem, The Pythagorean triple is expressed as a²+b² = c², where the perpendicular is a the base is b, and the hypotenuse is c of a right-angled triangle. Let us learn more about triples, their formula, list, steps to find the triples, and examples, in this article.
Pythagorean Triples in Maths
Pythagorean triples are basically the set of lengths of a right-angle triangle, defined as a²+b² = c², where a, b, and c are positive integers. According to the Pythagoras theorem, the square of the hypotenuse of a right-angle triangle equals the sum of the squares of the other two sides. It completely follow this theorem. These triples are denoted as (a,b,c). The most common and smallest Pythagorean triple is (3,4,5).
Pythagorean Triples Formula
Any three positive numbers that meet the Pythagorean theorem formula of a² + b² = c² are known as Pythagorean triples. Pythagoras was a mathematician notable for a property of triangles with a right angle, i.e. 90º angles.
The hypotenuse of a right-angled triangle is the side “r,” which is the side that faces the right angle. P and q are the two shorter sides that are adjacent to the right angle.
p² + q²= r²
In other words, The square of the longest side is equal to the sum of the squares on the other two sides of a Right angled Triangle.
Pythagorean Triples Examples
A Pythagorean triple is made up of three positive numbers, a, b, and c, such that a2 + b2 = c2. A triple like that is typically written (a, b, c) and the most basic and common triples are (3, 4, and 5). For each positive integer k, (ka, kb, kc) is a Pythagorean triple if (a, b, c) is one as well. The triplets in maths have an infinite set. The most basic and common triples are (3, 4, and 5). This allows us to produce a few more triples by taking values for k.
| K | (3k, 4k,5k) |
| 2 | (6, 8, 10) |
| 3 | (9, 12, 15) |
| 4 | (12,16,20) |
Pythagorean Triples List from 1 to 100
Check out 16 0rimitive Pythagorean triple lists from 1 to 100. You may solve numerical problems efficiently and quickly by memorizing these triplets in maths.
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Pythagorean Triples Proof
Consider the triples (5, 12, and 13) for which the Pythagorean formula [Hypotenuse2 = (side 1)2 +( side 2)2]can be verified.
The right-angled triangle’s hypotenuse has a length of 13, as it is the highest value among triples
L.H.S, Hypotenuse2=169.
The right-angled triangle’s other two sides = 5 and 12,
R.H.S, (side 1)2 +(side 2)2= 52 + 122 = 25+ 144= 169.
Hence, L.H.S=R.H.S [proved]
Pythagorean Triples Calculator
If we know only one length of the Pythagorean Triple, then we can find the other two lengths easily. The method of finding the length varies as There are two possible outcomes for the number: odd or even.
- In the case of an Odd Number
If the provided integer (n) is an odd number. The triples are of the form {n, (n2/2 – 0.5) and (n2/2 + 0.5)}
Consider the provided integer (n) is 7,
Then. the triples are{ (7, (72/2 – 0.5) and (72/2 + 0.5)}. Eventually, we do (7, 24, and 25)
- In the case of an Even Number
if the provided number (n) is an even number. Then. The triples have the following form: [n, (n/2)2-1), ((n/2)2+1)]
For instance, Consider the provided integer (n) is 8.
Then the triples are [n, (8/2)2-1), ((8/2)2+1)].
Eventually, we get triples (, 8,15, and 17)
Pythagorean Triples List
Check out the list of triples of numbers from 1 to 300 below
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
Pythagorean Triples List PDF
Pythagorean Triples are very useful while solving problems based on Trigonometry. Download the Triples List from 1 to 300 for future use.
Triplet Numbers
A triplet in mathematics generally refers to a set of three numbers, and there are different types of triplets depending on the context:
Pythagorean Triplets: These are three positive integers
a,b, and c that satisfy the equation
𝑎2 + 𝑏2 =𝑐2
For example, (3, 4, 5) and (5, 12, 13) are Pythagorean triplets.
Arithmetic Triplets: These are three numbers
a, b, and c that form an arithmetic sequence, meaning the difference between consecutive terms is constant:
b−a=c−b. For example, (1, 3, 5) is an arithmetic triplet.
Geometric Triplets: These are three numbers
a, b, and c that form a geometric sequence, meaning the ratio between consecutive terms is constant:
𝑏𝑎 =𝑐𝑏
For example, (2, 4, 8) is a geometric triplet.
Sum Triplets: In combinatorics, a triplet can refer to three numbers that sum to a specific value, often used in problems like finding three numbers in an array that add up to zero (or another target value).
Triples in Maths
Triples Maths are sets of three positive integers that satisfy the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In mathematical terms:
a^2 + b^2 = c^2
Where:
- ‘a’ and ‘b’ are the lengths of the two sides (legs) of the right-angled triangle.
- ‘c’ is the length of the hypotenuse.
Triples have a fascinating property of forming whole-number solutions to the Pythagorean theorem. Some of the well-known triples include:
- (3, 4, 5): 3^2 + 4^2 = 9 + 16 = 25 = 5^2
- (5, 12, 13): 5^2 + 12^2 = 25 + 144 = 169 = 13^2
- (8, 15, 17): 8^2 + 15^2 = 64 + 225 = 289 = 17^2
- (7, 24, 25): 7^2 + 24^2 = 49 + 576 = 625 = 25^2
- (9, 40, 41): 9^2 + 40^2 = 81 + 1600 = 1681 = 41^2
The above examples are just a few of the infinite number of triples that exist. There are various methods to generate triples, and one of the common techniques involves using the following formulas:
For any two positive integers ‘m’ and ‘n’ (where m > n):
a = m^2 – n^2 b = 2mn c = m^2 + n^2
By plugging these values of ‘a’, ‘b’, and ‘c’ into the Pythagorean theorem, we can verify that they form a Pythagorean triple. The values of ‘m’ and ‘n’ determine the particular triple obtained.
triplets in maths have applications in various fields, such as geometry, number theory, and cryptography. They also have practical uses in constructing right-angled triangles with specific side lengths, making them useful in various real-world scenarios and problem-solving situations.
Triplets in Trigonometry
In trigonometry, certain special angle values or ratios between sides of right-angled triangles are commonly referred to as important triplets. These triplets have specific trigonometric ratios that are frequently used in various trigonometric calculations and problem-solving. The three most important triplets in trigonometry are based on the angles 30°, 45°, and 60° and are associated with specific right-angled triangles. These triplets are as follows:
- 30-60-90 Triangle: In a 30-60-90 triangle, one angle measures 30 degrees, another angle measures 60 degrees, and the third angle is a right angle (90 degrees). The sides of this triangle have a specific ratio:
- The side opposite the 30° angle is half the length of the hypotenuse.
- The side opposite the 60° angle is (√3)/2 times the length of the hypotenuse.
- The hypotenuse (the side opposite the right angle) is the longest side and is twice the length of the side opposite the 30° angle.
Trigonometric Ratios: sin(30°) = 1/2 cos(30°) = (√3)/2 tan(30°) = 1/(√3)
- 45-45-90 Triangle: In a 45-45-90 triangle, both angles measure 45 degrees, and the third angle is a right angle (90 degrees). The sides of this triangle have a specific ratio:
- The two legs of the triangle are congruent and have the same length.
- The hypotenuse (the side opposite the right angle) is (√2) times the length of each leg.
Trigonometric Ratios: sin(45°) = (√2)/2 cos(45°) = (√2)/2 tan(45°) = 1
- 60-30-90 Triangle: In a 60-30-90 triangle, one angle measures 60 degrees, another angle measures 30 degrees, and the third angle is a right angle (90 degrees). The sides of this triangle have a specific ratio:
- The side opposite the 30° angle is half the length of the hypotenuse.
- The side opposite the 60° angle is (√3)/2 times the length of the side opposite the 30° angle.
- The hypotenuse (the side opposite the right angle) is twice the length of the side opposite the 30° angle.
Trigonometric Ratios: sin(60°) = (√3)/2 cos(60°) = 1/2 tan(60°) = √3
These important triplets play a significant role in various trigonometric calculations and are particularly useful for quickly finding trigonometric values of specific angles and in solving geometric problems involving right-angled triangles.
Related Posts
| Pythagoras theorem | 1 to 30 Squares & Cubes |
| Types of Angles in Maths | Natural Numbers |
| Profit and Loss Formula and Tricks | Volume of Cuboid |








 [Live Updates] NTA CUET Undergraduate Re...
[Live Updates] NTA CUET Undergraduate Re...
 IGNTU CUET Cutoff 2025, Check Category W...
IGNTU CUET Cutoff 2025, Check Category W...
 CGBSE Revaluation Result 2025 Announced ...
CGBSE Revaluation Result 2025 Announced ...









