What is the definition of Cuboid in maths ?

A cuboid is a three-dimensional figure or object in geometry that has six rectangular faces with eight vertices and twelve edges each. Examples of cuboids are lunch boxes, Bricks, Shoebox, Book, Carton boxes

How to determine volume of a cuboid?

the volume of a cuboid refers to the holding capacity of a cuboid. Basically, the volume of the cuboid refers to the amount that can hold by the cuboid. The Volume of a cuboid can easily determine by the formula = Length × breadth × height If we considered a cuboid having l length,h height, and b breadth. And Volume -V, then Volume of the cuboid (V) = l × b × h cubic units.

Volume of Cuboid Formula and Examples -

Table of Contents

Volume of Cuboid

The number of materials that a cuboid can transport or hold is known as the volume of cuboid, and it determines the holding capacity of a cylinder. We can determine volume of cuboid by the Volume of Cuboid formula V= l × b × h . In this article, we will learn about cuboids, their properties, and the Volume of a cuboid with some solved examples. we also know about the properties, surface area, and diagonals of a cuboid.

Cuboid

In geometry, A cuboid is a three-dimensional figure or object that has six rectangular faces, each of which has eight vertices and twelve edges.
Now imagine a shape made by stacking numerous congruent rectangles on top of one another. The resultant formed shape is known as a cuboid. In daily life, we observed different cuboid-shaped objects such as The lunch box, Bricks, Shoebox, Book, Carton boxes, and so on. As a cuboid is a three-dimensional solid object, Thus it has length, Height, and width. Let’s understand those quantities of a cuboid in the following diagram.

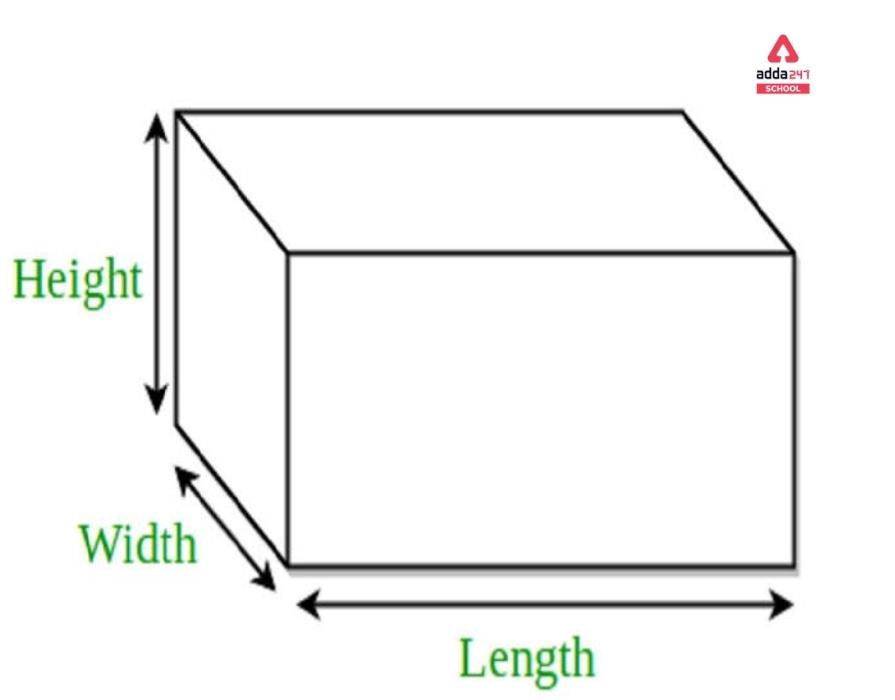
Properties of a Cuboid

The properties of a cuboid must be understood before learning about various cuboid quantities. such that we can quickly recognize a cuboid by its characteristics.
The main properties of a cuboid are listed below –
• There are 6 faces, 8 vertices, and 12 edges on a cuboid.
• The edges on either side of each other are parallel
• As a cuboid is a three-dimensional object, it has length, breadth, and height.
• A cuboid has only right angles that are produced at its vertices.
• The shapes of all the faces are rectangles.
• A cuboid has two diagonal lines that can be drawn on each face.

What is the Volume of Cuboid Formula?

A cuboid is a three-dimensional geometric shape with six rectangular faces, where opposite faces are parallel and equal in size. The volume of a cuboid can be calculated using the formula:

Volume = Length × Width × Height

Where:

Length refers to the length of the cuboid.
Width refers to the width of the cuboid.
Height refers to the height of the cuboid.

To calculate the volume of a cuboid, simply multiply its length, width, and height together. This formula works because the volume of a cuboid represents the amount of space enclosed by the three dimensions.

Volume of Cuboid Formula

Earlier we know that volume of cuboid refers to the holding capacity of a cuboid. Basically, the volume of a cuboid refers to the amount that can hold by the cuboid.
The Volume of cuboid formula = Length × breadth × height
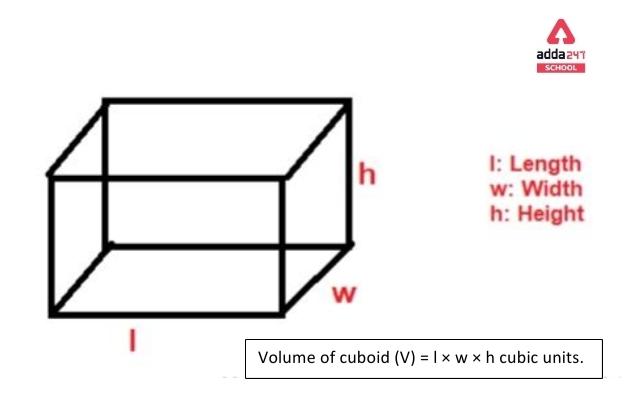
If we considered a cuboid having l length,h height, and b breadth. And Volume -V, then

Volume of cuboid (V) = l × b × h cubic units.

Units used to measure the volume of cuboid is –
Cubic Centimeters (cm³), Cubic meters (m³)

Volume of Cuboid Formula and Examples -_4.1 — Volume of cuboid Formula

Surface Area of a Cuboid

As a Cuboid is a three-dimensional figure, it has two types of surface area –
• Lateral surface area or LSA
• Total surface area or TSA

Lateral surface area of Cuboid Formula

The total area of all faces, excluding the top and bottom faces of a cuboid, is considered as Lateral surface area.
Lateral surface area = Sum of all 4 faces except the top and the top face of the cuboid.

If we took into account a cuboid with l length, h height, and b width. follows.

Lateral surface area (LSA) = 2h(l + b) sq.units

Total Surface Area Cuboid Formula

A cuboid’s surface area is the overall area that it takes up in its shape.
Total surface area (TSA ) equals the sum of the surfaces of all six rectangular faces

If we considered a cuboid having l length,h height, and b breadth. then,

Total surface area (TSA ) =2(lb + bh + hl) sq.units

Perimeter of Cuboid Formula

We know that a cuboid has 8 faces and 12 edges Perimeter is nothing but the sum of the lengths of all the 12 edges.
Taking into account a cuboid with dimensions of l length, h height, and b width. After that,
Perimeter of Cuboid = 4l + 4b + 4h

= 4× (l + b + h)

Perimeter of Cuboid (P) = 4× (l + b + h) units

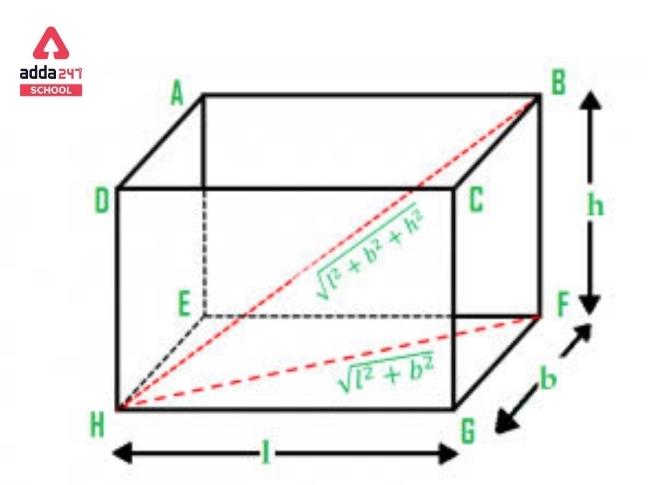
Diagonals of Cuboid Formula

A line segment that joins two of its opposed vertices and traverses the cuboid’s body, is known as a Diagonal cuboid Since a cuboid is a 3D shape, there are two types of diagonals in it:
• Face Diagonals
• Space Diagonals

Face Diagonals of Cuboid

Face Diagonals are considered as the line segment which is formed by connecting the opposite vertices of a certain cuboid face. Only two diagonals can be formed on each cuboid’s face.
A cuboid has a total of 12 face diagonals since it has 6 faces.

Space Diagonal of Cuboid Formula

A line segment that connects a cuboid’s opposing vertices is known as a space diagonal. The face diagonals have traversed the interior of the cuboid Thus it is possible to draw 4 space diagonals inside of one cuboid.

The Formulas to determine Diagonals of Cuboid
Face Diagonals of cuboid = √(l² + b²) units
Space Diagonals of Cuboid = √(l²+ b²+ h²) units

Whereas a cuboid’s three primary dimensions are its length (l), its width (b), and its height (h),

Volume of Cuboid Formula and Examples -_5.1 — Diagonals of Cuboid

Volume of Cuboid Formula and Other Related Formula

Here is a list consists all cuboid-related formulas in one place. We looked at a cuboid with the dimensions l length, h height, and b width.

Cuboid’s Quantities	Formulas
Volume of Cuboid	l × b × h cubic units.
Total Surface Area (TSA) of Cuboid	2(lb + bh + hl) sq.units
Lateral surface area (LSA) of Cuboid	2h(l + b) sq.units
Perimeter of Cuboid	4(l + b + h) units
Face Diagonals of Cuboid	√(l² + b²) units
Space Diagonals of Cuboid	√(l²+ b²+ h²) units

How to find the Volume of a Cuboid? Formula Based Solved Examples

Q. What is the volume of a cuboid with the dimensions 16 cm long, 12 cm wide, and 10 cm high?

Solution:

The cuboid’s length is 25 cm.

the cuboid’s width is 12 cm

The cuboid’s height is 16 cm.

As we know, the Volume of the cuboid = length× breadth × height.

V = (25 × 12 × 16) cm³

V = 4800 cm³( Answer)

Q. A cubical measures 8 meters long, 3 meters wide, and 10 meters high. Find the cubical’s volume.

Solution:

Length of the cubical – 8 meters.
cubical’s width – 3 meters
Cubical’s height -10 meters
Since the cubical’s volume is determined by its length, width, and height,
So now, volume = 8×3×10 m³
V = 240 m³ . ( Answer)

Q. Determine the total surface area of a cuboid having a length of 10 cm, a height of 12 cm, and a breadth of 8 cm.

As we know Total surface area (TSA ) = The sum of the surfaces of all six rectangular faces
If we considered a cuboid having l length,h height, and b breadth. then,
Total surface area (TSA ) =2(lb + bh + hl) sq.units
In the given problem,
Length (l)= 10 cm , breadth (b) = 8 cm ,height (h)= 12 cm .

Total surface area = 2[ ( 10×8)+(8×12)+(12×10)]
Or,TSA = 2 × (80+ 96+120)
Or, TSA = 592 cm² (Answer)

Related Post: