The Pythagoras theorem is one of the most crucial and fundamental concepts in mathematics. Pythagoras theorem is named after the Greek philosopher Pythagoras.
Pythagoras Theorem Class 10
Pythagoras theorem basically illustrates how a right-angled triangle’s sides are related to one another. The Pythagoras theorem states that the hypotenuse square of a triangle is equal to the sum of the squares of the other two sides. The Pythagoras theorem helps us to find out a triangle’s angle along with the length of the hypotenuse, perpendicular, and base of the right angle triangle. Here we learn more about the Pythagoras theorem, its formula, its equations, and derivations with solved examples, Let’s start learning…
Pythagoras Theorem Formula Class 10
Pythagoras theorem formula: Before learning the formula of Pythagoras theorem, let’s get a quick review of a right-angle triangle because the Pythagorean Theorem mainly shows how the sides of a right-angled triangle relate to one another. A right-angle triangle. Right angles always have a 90° angle. Hypotenuse, Base, and Perpendicular are the names of the three sides that make up a right angle. The longest side is always the hypotenuse. The hypotenuse is the side with the 90° angle opposite The other two inner angles add up to 90 degrees.
According to the Pythagoras theorem, the square of the hypotenuse of a right-angle triangle equals the sum of the squares of the other two sides. This theorem can be expressed as the Pythagorean equation, which is a relationship between the lengths of the three sides of a right angle triangle a, b, and the hypotenuse c.
Perpendicular2 + Base2 = Hypotenuse2
| a² + b² = c² |
let’s assume a triangle ABC, where BC² = AB²+ AC² is present. The base is represented by AB, the altitude by AC, and the hypotenuse by BC in this equation.
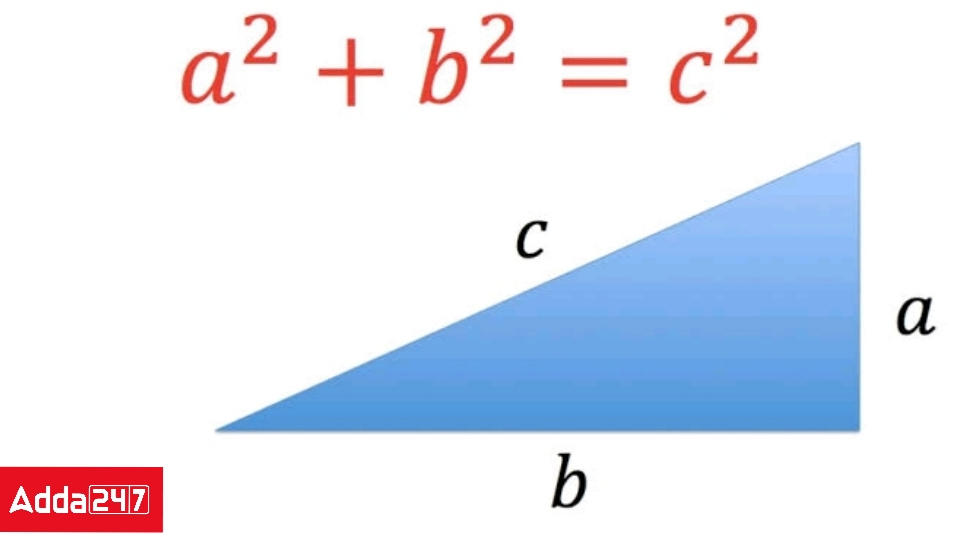
State Pythagoras Theorem
The Pythagoras theorem was first introduced by the Greek mathematician Pythagoras of Samos. He was a philosopher of the Classic Greek tradition. Born on the Greek island of Samos in 569 BC, Pythagoras of Samos travelled extensively in Egypt where he studied mathematics and other subjects. He established a community of mathematicians who practised strict discipline. Finally, the Greek mathematician proved the Pythagoras theorem; as a result, it is known as the “Pythagoras theorem” in his honour.
Pythagoras Theorem Proof for Class 10
There are numerous ways to demonstrate Pythagoras Theorem. The algebraic method and the method utilising similar triangles are two of the most popular methods to prove the Pythagoras theorem. To comprehend the proof of this theorem, let’s take a deeper look at each of these approaches separately.
Pythagoras Theorem Proof using Algebraic Method
The Pythagorean Theorem was proved using algebra using the diagram below. A big square and an inner square with sides equal to the hypotenuses of the four right triangles are constructed.
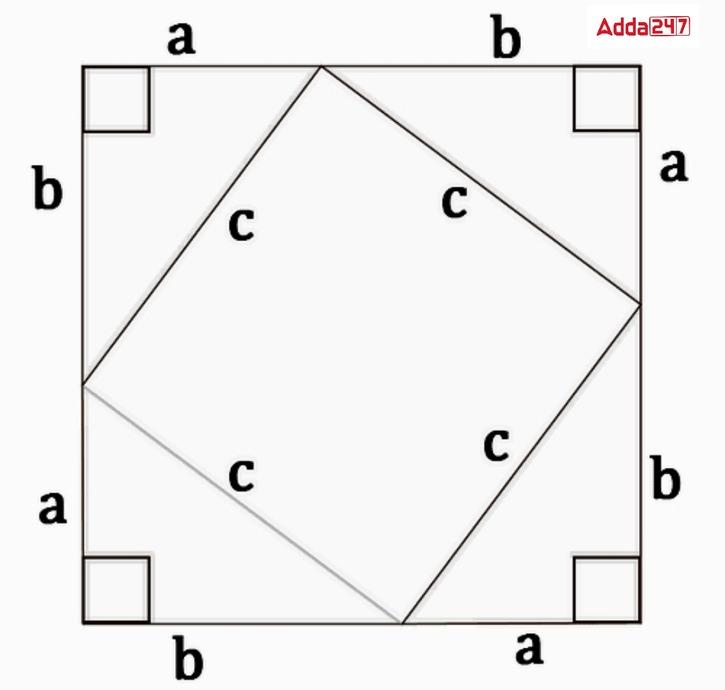
The triangles’ legs are of lengths a and b, and their hypotenuse is of length c.The sides of the big square that is produced measure (a + b). Its area is therefore equivalent to (a+b)²
Given that the length of the inner square sides is c, its area is. c².We can also observe that the area of the big square is the same as the sum of the areas of the four triangles and the inner square. As a result, we have:
(a+b)² =4(½×a× b) + c²
a² + b² +2ab = 2ab+ c²
a² + b² =c² (Proved)
Pythagoras Theorem Proof using similar triangles
When the corresponding sides and angles of two triangles are the same size and ratio, then we can say that both two triangles are similar. Let’s learn how we can prove the Pythagoras theorem using similar triangles.
- In a right triangle, the hypotenuse is divided into two pieces by an altitude taken from the right-angled vertex
- The two smaller right triangles that resulted are similar to one another.
- Measure the three triangles’ three sides collectively. The corresponding sides of the three triangles are proportional to one another because they are comparable triangles.
- Consider the ratios of the corresponding sides. From the equations, get the squares of the original triangle’s sides.
- Use the squares of the sides to prove the Pythagorean Theorem. Then, determine whether the sum is equal to the square of the hypotenuse.
Pythagoras Theorem- Pythagorean triples Explained
Pythagorean triples consist of the three positive numbers a, b, and c, where a2+b2 = c2. The symbols for these triples are (a,b,c). Here, a represents the right-angled triangle’s hypotenuse, b its base, and c its perpendicular. The smallest and most well-known triplets are (3,4,5).
| Pythagorean Triples Table | |||
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
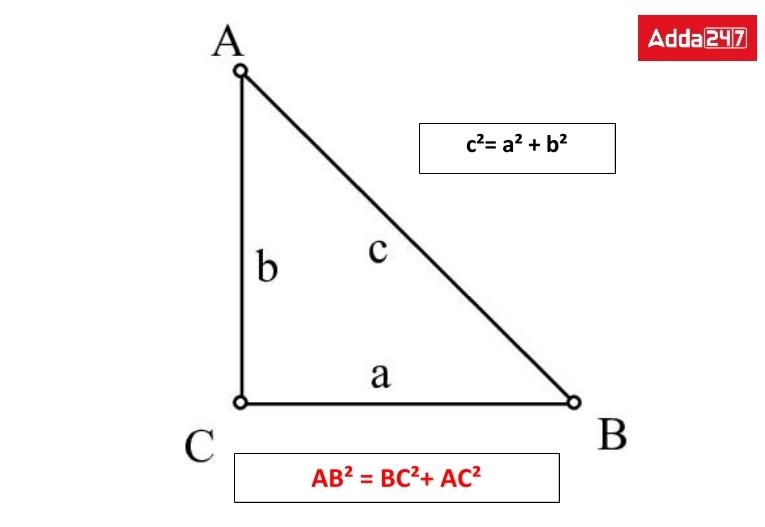
Pythagoras Theorem Derivation of Hypotenuse Formula
Imagine if the triangle ABC, which is right-angled at B. Create a perpendicular BD meeting AC at D. Use related triangles to prove the Pythagoras theorem.
In triangles △ABD and △ACB,
∠A = ∠A (common angle of both triangles)
∠ABC = ∠ADB (both angles are right angles)
Therefore, △ABD ∼△ACB (by AA similarity criterion)
We can also demonstrate similarly that△ BCD =△ ACB.
As a result,△ABD ∼ △ACB,
Henec, AD/AB = AB/AC. We can state that AD × AC = AB².
Similarly, we can prove that △BCD ∼ △ACB.
Hence, CD/BC = BC/AC Additionally, We can say, CD × AC = BC².
By combining these two equations, we obtain
AB² + BC² = (AD × AC) + (CD × AC)
AB²+ BC² =AC(AD +DC)
AB² + BC² =AC² [ Proved ]
Pythagoras Theorem Model
In a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides, according to Pythagoras’s Theorem. These triangle’s three sides are known as the Perpendicular, Base, and Hypotenuse.
This theorem can be expressed as the Pythagorean equation, which is a relationship between the lengths of the three sides of a right angle triangle a, b, and the hypotenuse c.
Perpendicular2 + Base2 = Hypotenuse2
| a² + b² = c² |
Pythagoras Theorem Image
Pythagoras Theorem Calculator
The main application of Pythagoras theorem is that it helps us to determine the lengths and angles of a right triangle. Along with mathematics, there are various uses of Pythagoras theorm in our real life as mentioned below. We express the pythagorus theorem in a simple Pythagoras equation, which is
Perpendicular2 + Base2 = Hypotenuse2
Or, a² + b² = c², where the lengths of the three sides of a right angle triangle a, b, and the hypotenuse c.
Pythagoras Theorem Applications
Several examples of how the Pythagoras Theorem is applied include
- The Pythagorean Theorem is frequently used to determine the lengths of a right-angled triangle’s sides. We can get the formula for the base, perpendicular, and hypotenuse using the Pythagoras Theorem.
- To determine the diagonal length of a rectangle, square, etc., use the theorem.
- A triangle’s correctness is determined using the converse of Pythagoras Theorem.
- In trigonometry, Pythagoras Theorem is used to determine trigonometric ratios such as sin, cos, tan, cosec, sec, and cot.
- In the disciplines of engineering and building, architects apply the Pythagoras Theorem approach.
- Applying the Pythagoras Theorem to mountain surveying
- Finding the shortest path is another application for it in navigation.
- Calculating how steep a mountain or hill’s slope requires the theorem.
Pythagoras Theorem Based Questions
Q.A triangle with two sides that are 4 cm and 3 cm long. what is the length of the hypotenous of the triangle?
Solution.According to formula of Pythagoras theorem ,Perpendicular2 + Base2 = Hypotenuse2
In the given problem, Base = 4 cm , Perpendicular = 3 cm.
As per the Pythagoras theorem,
Hypotenuse2 = 4 2 + 32
Hypotenuse2 = 16+ 9 = 25
Hypotenuse =√25 = 5 cm
Q.Given is a triangle with sides measuring 5 cm, 13 cm, and 12cm. Determine if these would make up the triangle’s right-angled sides.
Solution: A right-angled triangle with these sides must satisfy the Pythagoras theorem.
We must determine whether 52 + 122 = 132 [ Perpendicular2 + Base2 = Hypotenuse2 ]
Now, L.H.S= (52 + 122 )=(25 +144)= 169
R.H.S= (132 )= 169
L.H.S = R.H.S
So, this triangle fully satisfies the conditions of the Pythagoras theorem. So that it is a right-angle triangle.
Q. A triangle that has a hypotenosis of 17 cm and the base of 8 cm . Find the length of the perpendicular of the triangle.
Solution:
Length of the Base (a)= 8 cm
Length of the Hypotenous (c) = 17 cm
Let’s assume the length of the perpendicular is b cm.
According to Pythagoras theorem, a² + b² = c²
Or, b² = c² – a²
Or, b² = √( 17²- 8² )
Or, b = √ ( 289- 64) =√ 225
Or, b = 15
So,the length of the perpendicular is 15 cm.
Pythagoras Theorem Class 10 worksheet
Q.1.A ladder is placed 12 cm away from the wall such that the top of the ladder is 5 cm above the floor. Find the wall’s length.
Q.2.Given is a triangle with sides measuring 9 cm, 40 cm, and 41cm. Determine if these would make up the triangle’s right-angled sides.
Q.3.A triangle with two sides that are 16cm and 63 cm long. what is the length of the hypotenous of the triangle?








 BTEUP Result 2025 Out at bteup.ac.in, Do...
BTEUP Result 2025 Out at bteup.ac.in, Do...
 SGBAU Result 2025 Out, Check Summer Seme...
SGBAU Result 2025 Out, Check Summer Seme...
 How To Prepare for CUET Accountancy Exam...
How To Prepare for CUET Accountancy Exam...









