Types of Angles
In geometry, There are various types of angles. One of the most important and primary units is Angle. An angle is formed by when two rays or lines are joined at their common endpoint. Not only in maths we use angles in our daily life aspects, starting from a pizza slice to constructing buildings, dams, and statues. Angle is an integral part of Civil Engineering. In this article, we will learn about different types of angles and their properties in different aspects.
Definition of Angle for Class 5
Angles are the fundamental factors in geometry as well as daily life activities. When two rays or lines intersect at a common point, an angle is generated, and the size of each angle varies.
Basically, when two lines intersect at a common point, the measurement of the opening between two lines is known as the angle. Angle is represented by the symbol ∠.
Units used in the measurement of an angle are degree and radian.
Angles in Maths
In maths, angles are a fundamental concept that describes the amount of rotation or separation between two lines or line segments that meet at a common point, known as the vertex. Angles are typically measured in degrees (°) or radians (rad) and are used extensively in geometry, trigonometry, and various other branches of mathematics.
Here are some key concepts related to angles in maths:
- Types of Angles:
- Acute Angle: An angle that measures less than 90 degrees.
- Right Angle: An angle that measures exactly 90 degrees. It forms a perfect “L” shape.
- Obtuse Angle: An angle that measures more than 90 degrees but less than 180 degrees.
- Straight Angle: An angle that measures exactly 180 degrees. It forms a straight line.
- Reflex Angle: An angle that measures more than 180 degrees but less than 360 degrees.
- Angle Measurement Units:
- Degree (°): The most common unit of angle measurement, where a full circle is 360 degrees.
- Radian (rad): An alternative unit of angle measurement often used in trigonometry and calculus, where a full circle is equivalent to 2π radians.
- Complementary and Supplementary Angles:
- Complementary Angles: Two angles are complementary if their measures add up to 90 degrees. For example, 30 degrees and 60 degrees are complementary.
- Supplementary Angles: Two angles are supplementary if their measures add up to 180 degrees. For example, 120 degrees and 60 degrees are supplementary.
- Adjacent Angles:
- Adjacent Angles: Two angles are adjacent if they share a common vertex and a common side but have no common interior points. In other words, they are side by side.
- Vertical Angles:
- Vertical Angles: When two lines intersect, they form pairs of opposite angles called vertical angles. Vertical angles are congruent, meaning they have the same measure.
- Angle Bisector:
- Angle Bisector: A line or ray that divides an angle into two equal parts, creating two congruent angles.
- Exterior and Interior Angles:
- Exterior Angle: An angle formed by one side of a polygon and the extension of an adjacent side outside the polygon.
- Interior Angle: An angle formed by two sides of a polygon at a vertex inside the polygon.
- Trigonometry:
- Angles play a crucial role in trigonometry, where the study of the relationships between angles and the sides of triangles is essential. Key trigonometric functions include sine, cosine, tangent, cosecant, secant, and cotangent.
Understanding angles and their properties is fundamental in solving geometric problems and in various applications in physics, engineering, and other fields where spatial relationships and measurements are important.
Types of Angles in Maths
Angles are categorized based on their measurement as well as how they are rotated. Angles are classified as follows based on measurement. There are seven types of Angles commonly used in Mathematics:
- Zero Angle: (0° in Measure)
- Acute Angle: (0 to 90° in Measure) Less than 90°.
- Right Angle: Exactly 90°.
- Obtuse Angle: More than 90° but less than 180°.
- Straight Angle: Exactly 180°.
- Reflex Angle: More than 180° but less than 360°.
- Full Angle: Exactly 360°.
- Adjacent Angles: Two angles that share a common side and vertex.
- Complementary Angles: Two angles whose sum is 90°.
- Supplementary Angles: Two angles whose sum is 180°.
- Vertical Angles (Opposite Angles): Two angles that are opposite each other when two lines intersect; they are equal in measure.
Let’s get a brief idea of all of these types of angles.
Types of Angles with Degrees
We can classify angles based on two aspects –
•According to measurement
• According to the direction of rotation
● According to measurement –
based on angle measurement we can classify into 7 classes. Each angle has different identification and shape.
Let’s go through those 6 types and their properties.
1. Zero angle
Zero angles are formed when two rays of the angles are pointed in the same direction and rays start from a common point that measures exactly 0°.
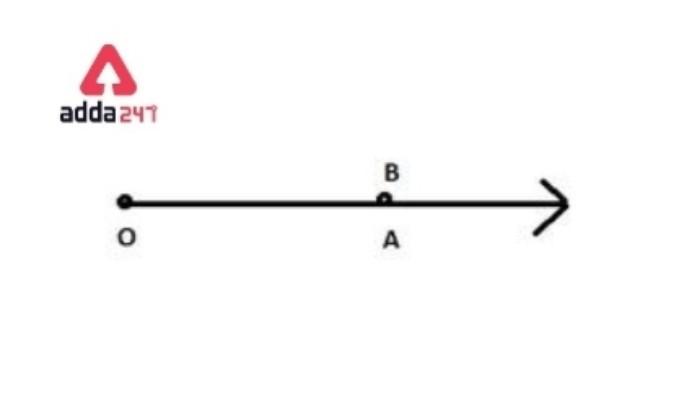
Zero angle
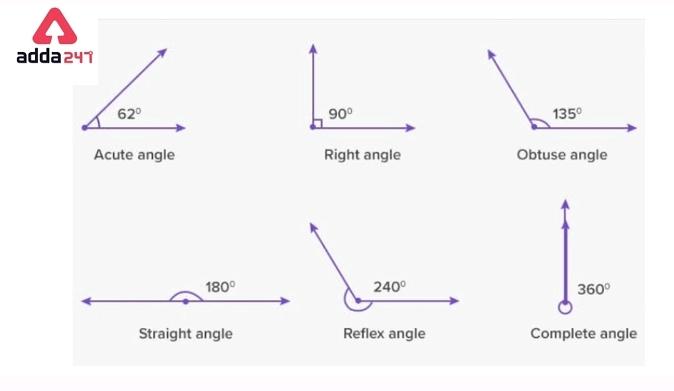
2. Acute Angle
An Angle that lies between greater than 0° and less than 90°, is known as an Acute angle.
0°<Acute angle >90°

3. Right Angle
The right angle looks like the English alphabet letter ‘L’ and can be easily observed. This angle is 90°.
Right angle =90°

4. Obtuse Angle
The angle in which the measurement is less than 180° but greater than 90° it is called an obtuse angle.
90°<Obtuse Angle >180°

5. Straight Angle
When intersecting two rays have formed an angle that measures exactly 180° is known as a Straight angle. It looks like a straight line that’s called so.
Straight angle – 180°

6. Reflex Angle
A reflex angle lies between greater than 180° and less than 360°.
180° < Reflex Angle >360°

7. Complete Angle
When an angle is exactly equal to 360°, this is called a complete angle.

Types of Angles in Maths for Class 5, 9
Here we provide a summary of the types of angles on the basis of degree-
| Types of angles | Angle measurement |
| Zero angle | Equals 0° |
| Acute angle | Greater than 0°, less than 90° |
| Right angle | Equals exactly 90° |
| Obtuse angle | Greater than 90°, less than 180° |
| Straight angle | Equals 180° |
| Reflex angle | Greater than 180°, less than 360° |
| Complete angle | Equals 360° |
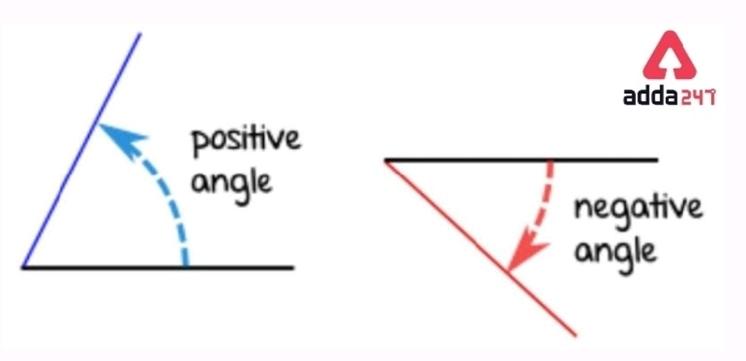
● According to the direction of rotation –
We can classify angles on the basis of the direction of rotation in two categories-
• Positive angles: If the measurement of the angles is to be done in the anti-clockwise direction starting from the base of the angle.
• Negative angles: Angles that are measured in the clockwise direction starting from the base of the angle.
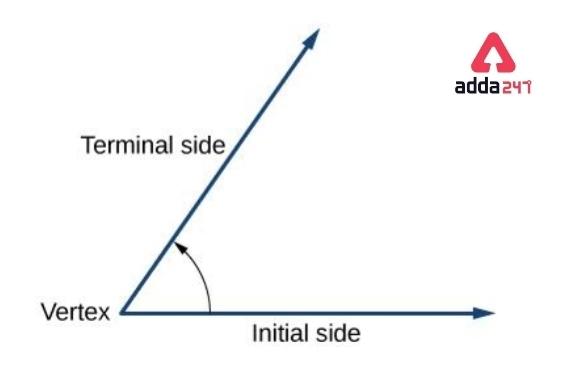
Angles Properties
Angles are generated when two lines intersect, and an angle is the space formed when two rays intersect at a single point. They are known as angle arms. Angles indicate how far a person has rotated from his original position. From an angle, There are mainly 2 parts –
• Vertex- In an angle, The common meeting point of the two lines is known as Vertex.
• Arms– Two lines or rays which intersect at a common point, are called arms. Two arms are -the terminal side and the initial side.
Pairs of Angles
Pairs of angles are described as When two angles appear in groups of two to display a certain geometrical property. There is some special relationship between those pairs of angles.
Some types of angle pairs are- complementary angles, supplementary angles, adjacent angles, vertical angles, and corresponding angles.
Types of Pairs of Angle
Some types of pairs of angles are –
Complementary angles–
When two angles are called complementary angles, it means the sum of their measures is 90°. Those types of angles complement each -other.

1,2 are adjacent complementary angles and 3,4 are non-adjacent complementary angles.
Supplementary angles
When the sum of two angles measures 180°. Those angles are the supplement of
the each other, is known as supplementary angles.

5,6 are adjacent complementary angles and 7,8 are non-adjacent complementary angles.
Adjacent angles
When two angles share a common vertex and side, They are called Adjacent angles.
Non-adjacent angles are formed if two angles have no common vertex or side.
Complementary and supplementary angles can be adjacent or nonadjacent angles.
vertical angles
When two lines or rays intersect in a common point and results four angles are formed. In those four angles, we observed that vertically present two opposite angles are equal, these pair of angles is called verticle angles.

corresponding angles
Corresponding angles are a pair of angles that forms when two parallel lines are intersected by a transversal.

Types of angles in parallel lines
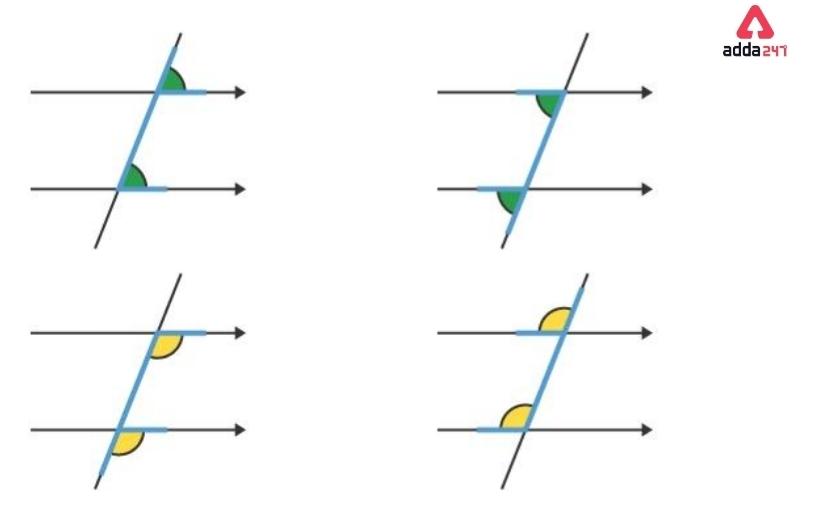
Types of Angles Based Exercises
Q. An angle that is greater than 180°, less than 360° is known as __
a) Right angle. b) Obtuse angle c) straight angle d) Reflex angle.
Answer- option (d)Reflex angle.
Because the Reflex angle lies between greater than 180° and less than 360°.
Q.In a pair of Supplementary angles one of the angle measures is 45°. What is the measurement of the other supplement angle?
a) 45° b) 130° ( c) 135 ° (d) None of those
Answer- we know that In a pair of supplementary angles, the sum of two angles is 180°.
In given supplementary angles, one angle is 45°.
Then the other angle is (180°-45°) = 135°
Option ( c) is correct.
Q.In a pair of complementary angles one of the angle measures is 30 °. What is the measurement of the other complement angle?
a) 150° b) 60° ( c) 90 ° (d) None of those
Answer- In Complementary angles, it means the sum of their measures is 90°.
In given complementary angles, one angle is 30°.
Then the other angle is -(90°-30°) = 60°
Hence option (b) is correct.
Q.An Angle P measures 150° in protractor. In Which category of angle does Angle P fall?
a) Right angle. b) Obtuse angle c) straight angle d) Reflex angle.
Answer: Angle P fall between 90° and 180°.We know that angle that lies between less than 90° and greater than 90° is called an obtuse angle.
Therefore angle P is an obtuse angle.
Q. In a protractor, an Angle X measures 20°. Which type of angle does Angle X belong to?
a) Right angle. b) Obtuse angle c) Acute angle d) Reflex angle.
Answer- Angle X lies between 0° and 90°.
An Angle Which angle measures greater than 0° but less than 90°, is known as an Acute angle.
0°<Acute angle >90°
Therefore, angle X is an Acute angle.
Q. An angle that is greater than 90°, less than 180° is known as __
a) Right angle. b) Obtuse angle c) straight angle d) Reflex angle.
Answer- option( b) Obtuse angle
An obtuse angle lies between less than 180° and greater than 90°.
Types of Angles Class 9 Worksheet
- An Angle Z measures 183 ° in the protractor. In Which category of angle does Angle Z fall?
- In a pair of complementary angles, one of the angle measures is 80°. What is the measurement of the other complement angle?
- An angle that is greater than 0°, less than 90° is known as __
- An Angle W measures 75 ° in the protractor. In Which category of angle does Angle W fall?
Related Post
- Types of Triangles
- Area Of Equilateral Triangle Formula With Height
- Adjacent Angles -Definition, Properties, Examples









 Try CUET College Predictor 2025 to Predi...
Try CUET College Predictor 2025 to Predi...
 CUET Result 2025 OUT (Today) @cuet.nta.n...
CUET Result 2025 OUT (Today) @cuet.nta.n...
 Why the Delay in CUET UG 2025 Results? C...
Why the Delay in CUET UG 2025 Results? C...









