Adjacent Angles -Definition, Properties, Examples

What are Adjacent angles?

Adjacent Angles are one of the types of angles in Geometry. Adjacent Angles are two angles that share a common side and a common vertex (Corner point) but do not overlap. When adjacent angles have a common vertex and side, they can be complementary angles or supplementary angles. Let us learn about the Adjacent angle’s definition, properties, Examples, and many more.

Read: Types of Angles in Maths, with Definition, Degrees & Examples

Adjacent Angles Meaning

As the name “Adjacent Angles” Suggests, Angles are always situated next to one another. When two angles have a common vertex and side, they are referred to as adjacent angles. The vertex of an angle is the point at which the rays that make up its sides come to an end. When two straight lines cross, four angles are formed, with the intersection point serving as the vertex of each. The term “adjacent angles” refers to two angles that have a common vertex and side.

Check: What is Scalene Angles?

Adjacent Angles Definition

When two angles share a common vertex and a common side, those angles are known as Adjacent Angles. When two rays intersect at a shared endpoint, Adjacent Angles are formed that are always positioned next to one another positioned but they don’t cross over each other. Observe the below figure of adjacent angles for better understanding. In the below figure, ∠a and ∠b are adjacent angles that share a common vertex and a common side.

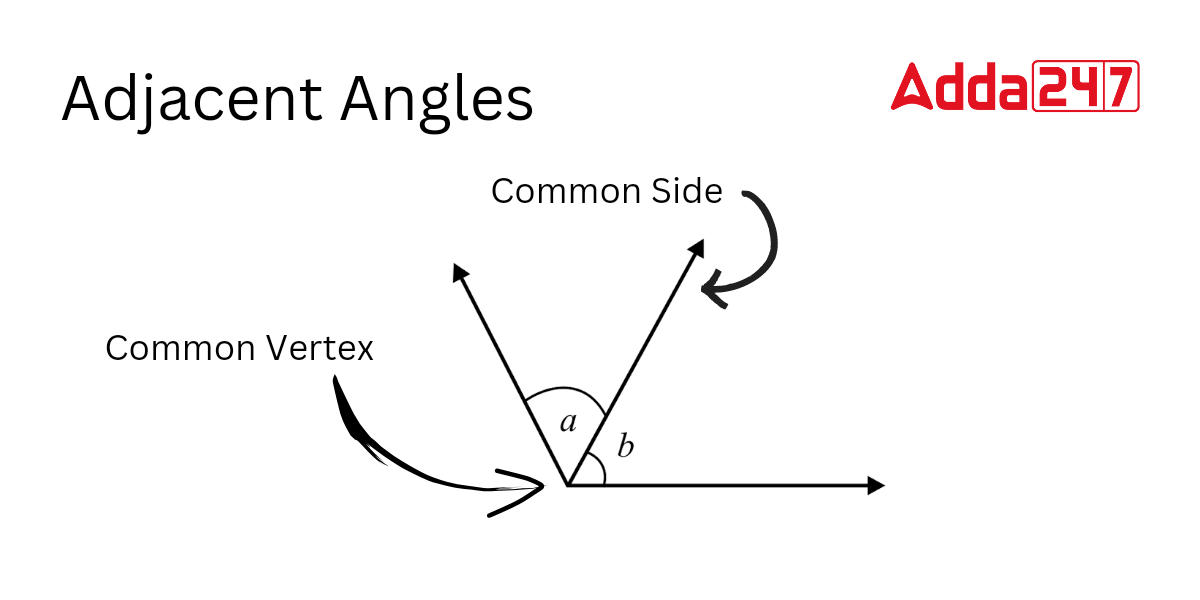
Adjacent Angles Examples in Real Life

There are numerous examples of adjacent angles in everyday life.

1. Most of us loved to eat pizza. Adjacent angles are formed when two pizza slices are placed next to one another. This is the most typical real-world example of adjacent angles.
2. When all three are separated from one another in a wall clock. The minute hand and second hand of the clock make one angle, and the hour hand and second hand make another angle. These two simultaneous angles are referred to as adjacent angles because they are close to one another.

Properties of Adjacent Angles

The properties of adjacent angles are listed below to make it simple to recognize them. The properties of adjacent angles are as follows

1. A common arm is always shared by adjacent angles.
2. They are associated with a common vertex.
3. They don’t cross over each other or overlap.
4. On either side of the common arm, they have a non-common arm.
5. They are not connected by an interior point.
6. Depending on the total of the individual angles’ measures, two adjacent angles can be supplementary or complementary.

How to Identify Adjacent Angles?

Earlier we know from the properties of adjacent Angles, that adjacent angles are always shared with a common vertex and a common side. we can easily identify adjacent angles using these properties. Any two angles are not regarded as adjacent angles if they only meet one of these criteria. Both of these properties must be satisfied by the angles.

Supplementary Adjacent Angles

If the sum of two adjacent angles is 180 degrees, then those angles are shown to be supplementary angles. Two supplementary angles are considered to be linear pairs if they are next to one another. The non-common arms form a line if the sum of two adjacent angles is 180°.
Sum of two adjacent supplementary angles = 180º

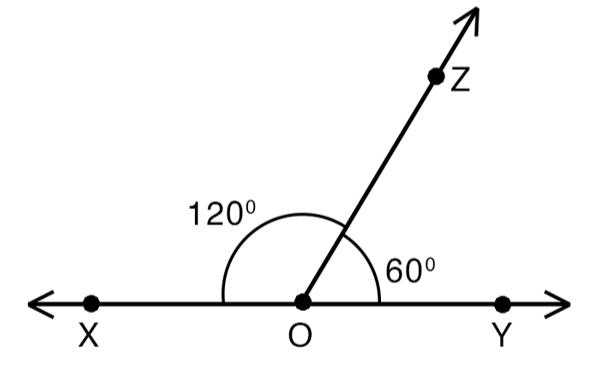
Complementary Adjacent Angles

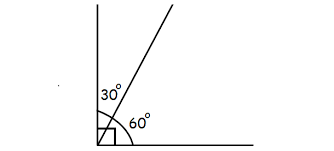
If the sum of the Adjacent angles that share a common vertex and a common Side is 90º, then the adjacent angles are called Complementary Adjacent Angles.

In the below the figure, two angles that measure 60º and 30º respectively id known as Complementary Adjacent Angles.

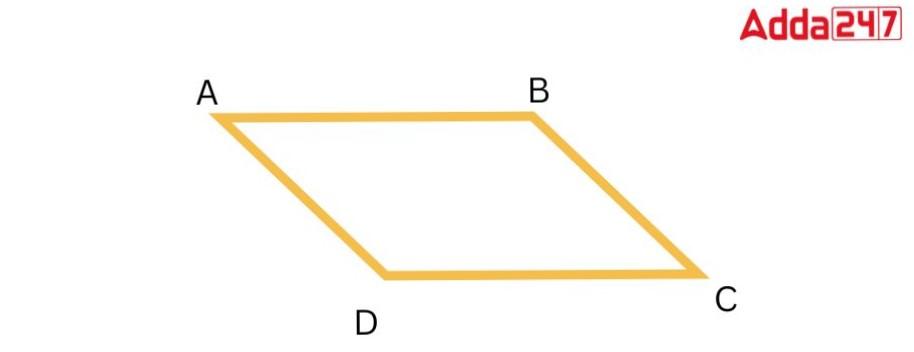
Adjacent angles of a parallelogram are

A quadrilateral with two sets of parallel sides is referred to as a parallelogram. In a parallelogram, the opposing sides are of equal length, and the opposing angles are of equal size.is the sum of all interior angles.is 360 degrees.  Additionally, the interior angles that are supplementary to the transversal on the same side.

In the below parallelogram named ABCD. Which adjacent angles are ∠A and ∠B, ∠B and ∠C,∠C and ∠D.and ∠A and ∠D

As the properties of a parallelogram, the interior adjacent angles are supplementary, meaning the sum of two adjacent angles is 180 degrees. Consequently, a parallelogram’s adjacent angles are supplementary.

Adjacent Angles-FAQs

Q.What do you mean by Adjacent Angles?

When two angles share a common vertex and a common side, those angles are known as Adjacent Angles. When two rays intersect at a shared endpoint, Adjacent Angles are formed that are always positioned next to one another positioned but they don’t cross over each other.

Q.What is required for an adjacent angle?

Adjacent Angles are two angles that share a common side and a common vertex (Corner point) but do not overlap.
Q.How do you identify adjacent?

Ans: When two straight lines cross, four angles are formed, with the intersection point serving as the vertex of each. The term “adjacent angles” refers to two angles that have a common vertex and side.

Sharing is caring!