What is the formula for Perimeter of an Equilateral triangle ?

If the length of one side is a units. The formula for perimeter of an Equilateral Triangle is – P= (a +a+ a) = 3a

Area of Equilateral Triangle Formula with Height

Q: What is an Equilateral Triangle ?

Equilateral triangle is a triangle which have three equal sides and all of its internal angles are same measure , equal to 60 degree each.

Table of Contents

Area of Equilateral Triangle

In this article, we will learn about an Equilateral Triangle and the Area of the Equilateral Triangle. In geometry, we find different types of triangles. Among those triangles, the most simple type of triangle is the equilateral triangle. The equilateral triangle is a triangle that has three equal sides.

Here we will learn about the formula for the area of an equilateral triangle and solve some questions based on the equilateral triangle

What is an Equilateral Triangle ?

The name suggests, that “equi” means equal. All three sides of an equilateral triangle are equal lengths and all of its internal angles are the same measure, equal to 60 degrees.

Area of an Equilateral Triangle is Equal to

Area of an equilateral triangle defines as the surface area which Is covered by the three sides of that triangle. The area of an equilateral triangle is Expressed by square units. It is easier to find the area if length of one side of the triangle is known.

Area of Equilateral Triangle Formula

The area of an Equilateral triangle means the amount of area occupied by the triangle in a 2D plane.By the following formula, we can calculate the area of an Equilateral triangle –

Area = √(3/4) × (side)² square units

Let, the length side of the triangle is – a units

Then, Area = √(3/4) × (a)² square units

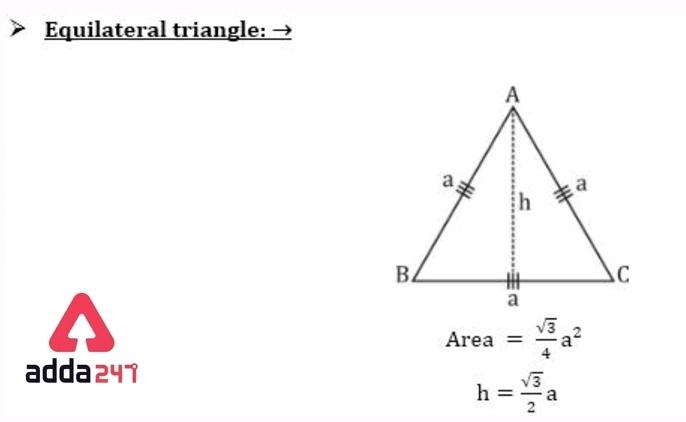
Area of Equilateral Triangle Formula Proof

Let, the length side of the triangle is – a units

Formula for Area of a Triangle is

Area =1/2 ( base ×height)

Now, In an Equilateral triangle, draw a perpendicular from vertex to the base which results in the triangle dividing into two equal right-angled triangle.

Now, one of the right-angled triangles will have base (a/2) units [ total base length of equilateral is a unit] and the length of hypotenuse length is ‘ a’ units.

Let, the length of perpendicular – ‘ h ‘ units

Hypotenuse ²= Base² + Perpendicular² ( by Pythagorean theorem )

Perpendicular² = Hypotenuse² -Base²

h²= a² – (a/2)²

h² =(3a²) /4

So, height = 3√a/2

Now ,

Formula for area of a Triangle is =1/2 ( base ×height)

A = ½ ( a × 3√a/2 )

[ where Base – a & height – (3√a)/2]

Or, A= (3√a)/ 4 [proved]

Formula for Perimeter of an Equilateral Triangle

Perimeter of an equilateral triangle represents as the sum of lengths of the all the equal sides of the equilateral triangle.

Let the length of one side is a units.

Perimeter of an Equilateral Triangle is – P= (a +a+ a) = 3a units

How to find the area of an equilateral triangle with height?- Solved Examples

Q. Find out the total area of an equilateral triangle with sides 12 cm.

a) 12√3cm² b)54√3cm² c) 36√3cm² d) None of these

Ans- Formula for area of equilateral triangle is

Area – √(3/4) × (side)²square cm.

Length of the sides in given equilateral triangle is 12 cm

Area = √(3/4) ×12²

= √(3/4) × 144

= 36√3 cm²

So, option( c ) is correct .

Q. Calculate the area of given equilateral triangle with base length of 8 cm.

a) 16√3cm² b) 64√3cm² c) 8√2cm² d) None of these

Ans- We know that all the three sides of an equilateral triangle are equal in length.

Now,

Area of equilateral triangle is = √(3/4) ×(side)² square cm

Length of one side is 8 cm.

Area = √(3/4) ×8²

= √(3/4) × 64

= 16√3 cm²

So, option ( a ) is correct

Q.Calculate the perimeter of given equilateral triangle with sides 15 cm.

a)15 cm b)45 cm c) 30 cm d) None of these

Ans – Perimeter of an Equilateral Triangle is – P= (a +a+ a) = 3a units

Here , Length of one side is 15 cm.

Perimeter ( P) = 3a = 3 × 15 = 45 cm

So, option ( b ) is correct

Area of Equilateral Triangle in Hindi

समबाहु त्रिभुज का क्षेत्रफल: इस लेख में हम एक समबाहु त्रिभुज और समबाहु त्रिभुज के क्षेत्रफल के बारे में जानेंगे। ज्यामिति में हमें विभिन्न प्रकार के त्रिभुज मिलते हैं। उन त्रिभुजों में, सबसे सरल प्रकार का त्रिभुज समबाहु त्रिभुज है। समबाहु त्रिभुज एक त्रिभुज है जिसमें तीन समान भुजाएँ होती हैं।

यहां हम समबाहु त्रिभुज के क्षेत्रफल के सूत्र के बारे में जानेंगे और समबाहु त्रिभुज पर आधारित कुछ प्रश्नों को हल करेंगे

एक समबाहु त्रिभुज क्या है?

नाम से पता चलता है, कि “इक्वि” का अर्थ बराबर है। एक समबाहु त्रिभुज की तीनों भुजाएँ समान लंबाई की होती हैं और इसके सभी आंतरिक कोण समान माप के होते हैं, जो 60 डिग्री के बराबर होते हैं।

एक समबाहु त्रिभुज का क्षेत्रफल

एक समबाहु त्रिभुज का क्षेत्रफल उस सतह क्षेत्र के रूप में परिभाषित होता है जो उस त्रिभुज की तीनों भुजाओं से ढका होता है। एक समबाहु त्रिभुज का क्षेत्रफल वर्ग इकाइयों द्वारा व्यक्त किया जाता है। यदि त्रिभुज की एक भुजा की लंबाई ज्ञात हो तो क्षेत्रफल ज्ञात करना आसान होता है।

Area of Equilateral Triangle ka Formula

एक समबाहु त्रिभुज के क्षेत्रफल का अर्थ है एक 2D तल में त्रिभुज द्वारा व्याप्त क्षेत्रफल की मात्रा। निम्नलिखित सूत्र द्वारा, हम एक समबाहु त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं –

क्षेत्रफल = √(3/4) × (भुजा)² वर्ग इकाई

माना, त्रिभुज की लंबाई भुजा है – a इकाई

तब, क्षेत्रफल = √(3/4) × (a)² वर्ग इकाई

Related Post:

Area of Equilateral Triangle Formula with Height is Equal to- FAQs

Q. What is an Equilateral Triangle?
A. Equilateral triangle is a triangle that has three equal sides and all of its internal angles are the same measure, equal to 60 degrees each.

Q. What is a formula for the area of the Equilateral Triangle?

A. → Area of an equilateral triangle defines as the surface area which Is covered by the three sides of that triangle.
Area = √(3/4) × (side)^2 square units

Q. What is a formula for the perimeter the Equilateral Triangle?

A. If the length of one side is a unit.
The formula for perimeter of an Equilateral Triangle is – P= (a +a+ a) = 3a

Q. What is the value of total angle of an equilateral is equal to?

A. Equilateral triangle has three angles which are same in measurement, equals to 60° each for a total of 180 degrees .

Q. What are the properties of an equilateral triangle?

A. Equilateral triangle has main two properties are-all the three sides are equal in length and all three angles are same in measurement, equal to 60° each.