Types of Triangles: The triangle is one of the most universal geometrical forms that we encounter in our daily lives. All types of triangles are polygons with three sides. The vertex is the place where two triangle sides meet and produce an interior angle. All internal angles formed by a triangle’s sides are always 180 degrees. Triangles have three sides, three vertices, and three internal angles in total. In terms of the length and measurement of a triangle’s sides and angles, there are 6 different types of triangles. Continue reading the full article to have a better understanding of the many types of angles based on sides and angles.
Types of Triangles
As previously stated, all types of triangles is a closed two-dimensional shapes having three sides. The sum of a triangle’s internal angles will always equal 180 degrees. This is known as the angle sum property of a triangle. All polygons can be subdivided into triangles, or constructed by merging two or more triangles. It can be divided into two types based on their bases, one based on the sides and the other on the internal angles of triangles. various types of triangles have various properties.
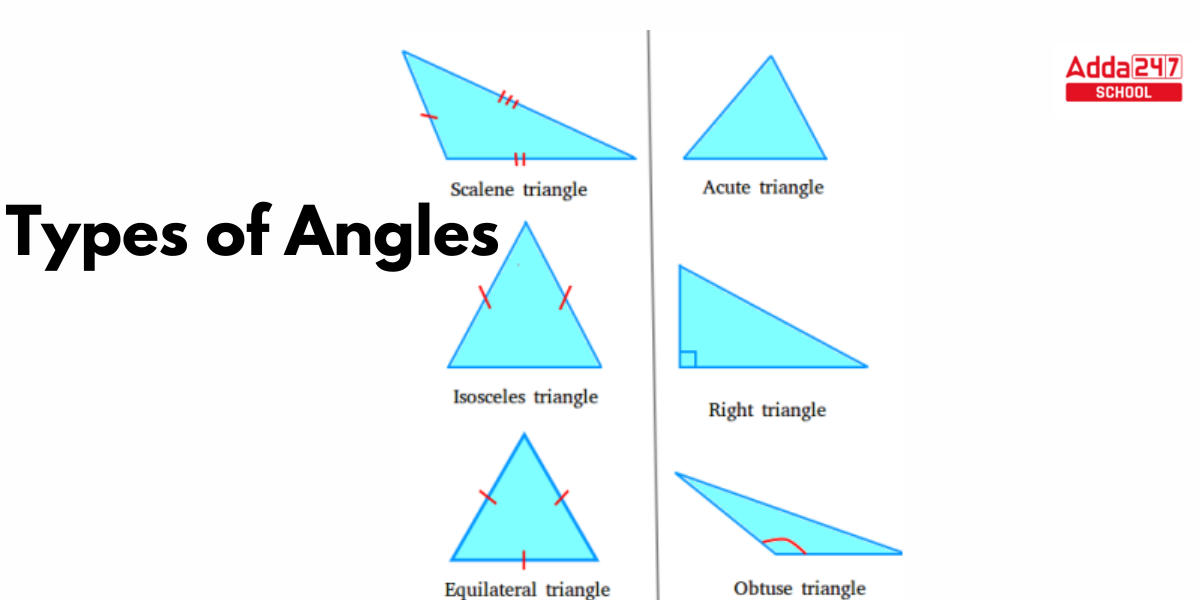
Types of Triangles with Properties
All the important types of triangles with properties are discussed in this section.
- A triangle is made up of three sides. The sum of the lengths of both sides of any type of triangle exceeds the length of the third side. The triangle inequality property is another name for this.
- A triangle has three internal angles, and the sum of those inner angles is 180°. This is known as a triangle’s angle-sum property.
- A triangle’s outer angle is always proportional to the sum of its inner opposite angles. This is known as a triangle’s outside angle property.
- The longest side of any triangle is opposing the largest angle, while the shortest side of any kind of triangle is opposite the smallest angle.
- A triangle’s perimeter is equal to the sum of its three sides.
- Area of a triangle = ½ × Base × Height
- Two triangles are considered to be similar if their corresponding angles are congruent and their side lengths are proportionate.
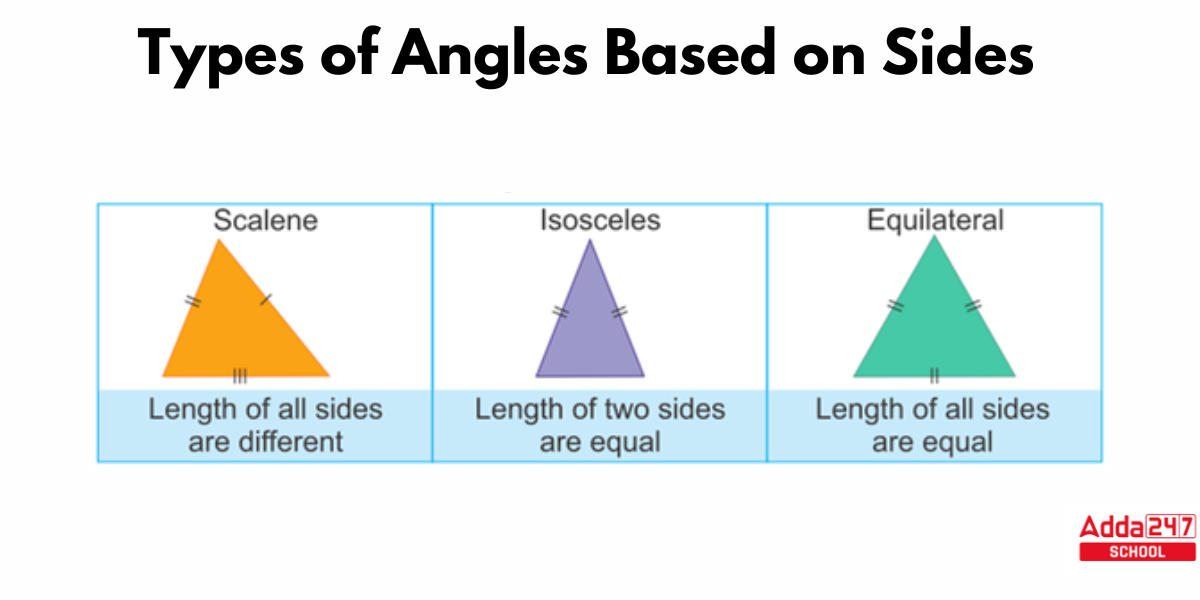
Types of Triangle on The Basis of Sides
The many types of triangles have distinct names. Three types of triangles—scalene, isosceles, and equilateral are distinguished by the length of their sides. Students can see the image of three types of Triangles Based on the Sides given below section.
| Types of Triangles on the Basis of Sides |
| Scalene Triangle |
| Isosceles Triangle |
| Equilateral Triangle |
Types of Triangle Based on Sides in Details
Triangles are classified based on the varied characteristics of their internal angles. The various types of triangles based on angles are detailed further below.
Scalene Triangle
A scalene triangle’s sides are of various lengths. As a result, the three interior angles differ from one another. A scalene triangle is seen in the diagram above. You can see that none of the sides are the same length. In the diagram above, students are able to observe that all of the triangle’s sides appear to be unequal.
Isosceles Triangle
Two of the three sides of an isosceles triangle are equal in length. As a result, the angles opposing the equal sides are equal. An isosceles triangle, in other words, has two sides that are equal and two equal angles. The diagram above depicts an isosceles triangle. The two sides of the triangle appear to be equal in the illustration above, but the base of the triangle is smaller than the other two sides.
Equilateral Triangle
An equilateral triangle has three sides that are of the same length. As a result, each interior angle of an equilateral triangle equals 60°. An equilateral triangle is additionally referred to as an equiangular triangle since its angles are all the same. The third diagram above depicts an equilateral triangle.
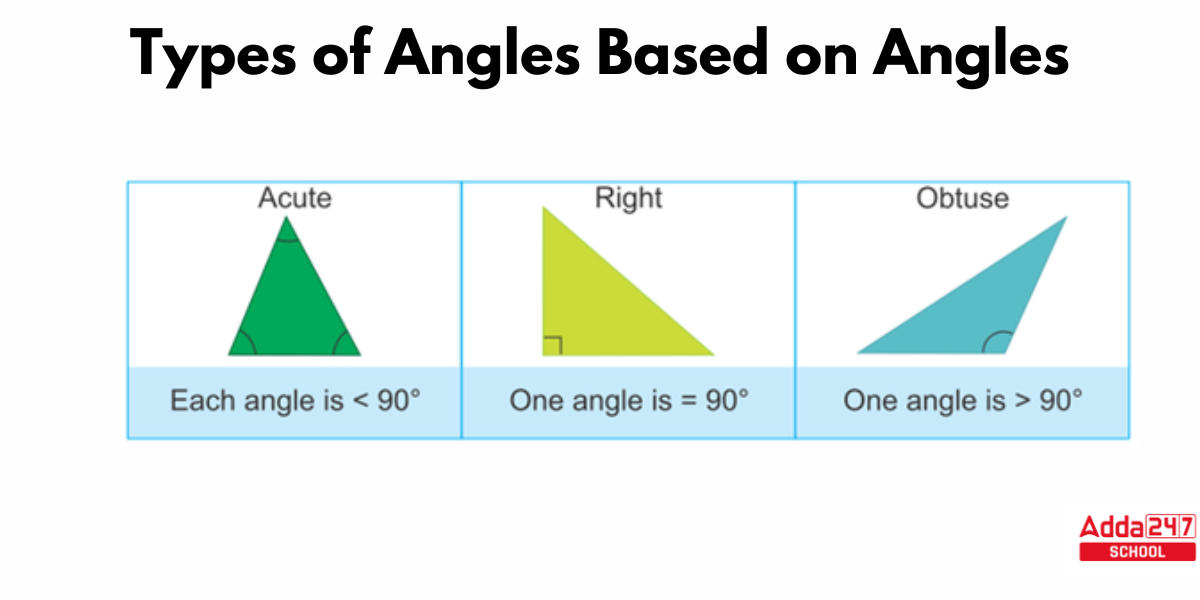
Types of Triangles on the Basis of Angles
Angles are classified according to their measurement in geometry. The nomenclature of a triangle is also determined by the measure of its internal angle: acute (if all angles are less than 90°), right (if one angle is 90°), and obtuse (if one angle is more than 90°). As demonstrated in the image below, the internal angles of a triangle can be acute, right, or obtuse.
| Types of Triangles on the Basis of Angles |
Types of Triangles Based on Angles
Here we have the 3 types of angles based on their angles.
Acute Triangle
An acute-angled triangle is one that has all acute interior angles, that is, angles that are fewer than 90 degrees. Above first is a diagram of an acute-angled triangle. All of the inner angles of the triangle in the above figure are fewer than 90 degrees, indicating that it is an acute triangle.
Obtuse Angled Triangle
An obtuse-angled triangle is one that has one obtuse angle (one that is more than 90 degrees) out of its three internal angles. The third one in the picture is an obtuse triangle.
Right Angled Triangle
A right triangle is one that has one right angle, which is a 90-degree angle, out of its three interior angles.
- The hypotenuse is the longest side of this right-angled triangle.
- The side opposing the 90-degree angle is the longest side of this triangle, while the other two sides are relatively smaller.
- A right isosceles triangle has two equal sides and two equal angles with 90-degree angles.
| Related posts | |
| Types of Angles in Maths, with Degrees | Area of Triangle Formula |
| Trigonometry Formulas | Perimeter of Triangle- Formula |
| Types of Bank | Types of Software |









 Madras University Result 2025 OUT at uno...
Madras University Result 2025 OUT at uno...
 CUET Geography Important Topics 2026 | B...
CUET Geography Important Topics 2026 | B...
 BCECE LE 2025 Counselling Dates Out, Che...
BCECE LE 2025 Counselling Dates Out, Che...









