Right Angle Triangle

Table of Contents

Right Angle Triangle: One of the most useful forms in Geometry is the right angled triangle. A right angled triangle is a triangle that contains a right angle (90°). In mathematics, we examine numerous types of triangles such as equilateral, isosceles, scalene, and right-angled triangles. The symbol for a right angle triangle is -the small square in the corner indicates that it is a right angled triangle. This article will go through right angled triangles, types of right angled triangles, right angled triangle properties, right angled triangle area, perimeter formula, and other topics.

Right Angle Triangle

Right Angle Triangle is also known as a Right Triangle. What is a Triangle? A triangle is a polygon having the smallest number of sides allowed to make a polygon. The word Triangle refers to a polygon with three sides, three vertices, and three angles. It is possible to say that any closed figure with all three sides and the sum of all 3 internal angles equals 180°.
In trigonometry, the right Angle triangle is very significant. It is employed in the Pythagoras Theorem and Sine, Cosine, and Tangent for instance. A right angle triangle, as the name implies, is a triangle with one right angle (90°). In the next sections, we will dig more into the topic of right angle triangles.

Right Angle Triangle Definition & Meaning

A Right Triangle is a triangle with any inner angle equal to 90°. Right triangles are further classed as isosceles right triangles and scalene right triangles based on the additional angle values. The Pythagorean theorem can be used to readily understand the connection that exists between the various sides of this triangle. The Angle Sum Property of a Triangle states that the sum of all the internal angles of a right-angle triangle is 180°. As a result, if any of the triangles is 90°, the sum of the other two angles is also 90°. The side opposing the right angle is the longest and is known as the hypotenuse.

Right Angle Triangle Diagram

Here is an illustration of a right angle triangle given below –

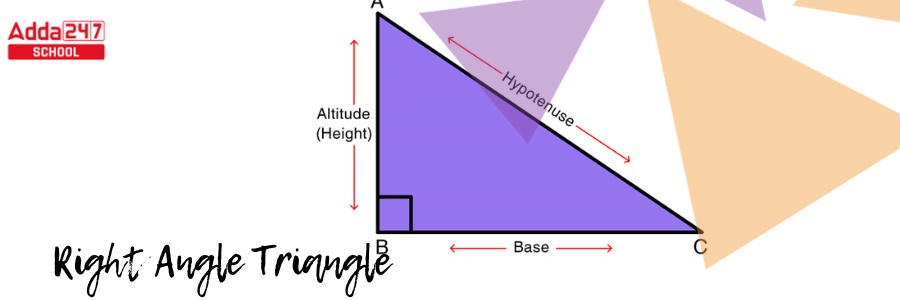
Right Angle Triangle Types

There are mainly 2 types of right angle triangles, including isosceles and scalene right triangles. One of the angles in these right angle triangles is 90°, as we have taught. But the triangle’s other two angles will turn into acute angles. So let’s understand the two types of Right Angle Triangle / Right Angle here.

Right Isosceles Triangle

In the Right Isosceles triangle, one internal angle in this triangle is 90°, and the other two angles are 45° each. A 90º-45º- 45º triangle is another name for an isosceles right triangle.

Examine the triangle below, where angle one angle is 90°, and we can see that the other two angles are 45º. Because the triangle has two equal sides, it is also an isosceles triangle.

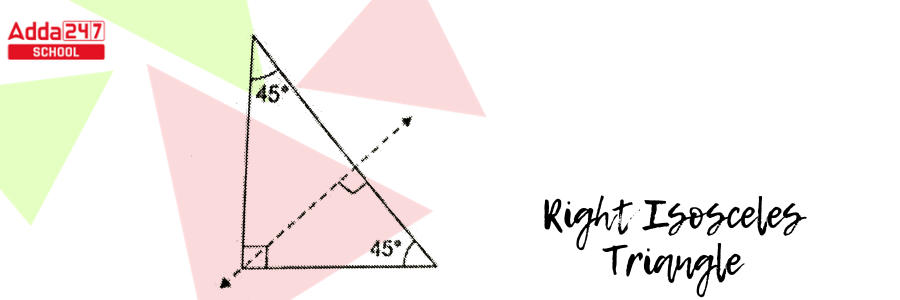
The total of a triangle’s angles is 180º. As a result, the base angles sum up to 90°, implying that they are 45° each. So the angles in an isosceles right triangle are always 90º-45º- 45º.

Right Triangle Scalene

Right Triangle Scalene triangle has one inner angle that measures 90°, but the other two have differing measurements.

As an example: ∠B measures 30°, ∠A measures 90°, and ∠C measures 60° in the scalene right triangle CAB. All three sides of this triangle will be different lengths, and the three angles will be different sizes.

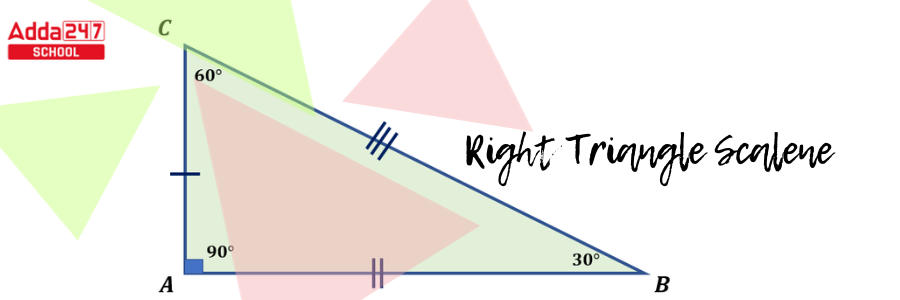
There is also a specific case of a scalene triangle 30°-60°-90°, which is similar to a right triangle and has a length-to-length ratio of 2:1. The side opposite the 30º angle is the shortest.

Right Angle Triangle Formula

A right-angled triangle is a triangle in which one of the angles is 90 degrees. The sum of the other two angles is 90 degrees. The sides comprising the right angle remain perpendicular and form the triangle’s base. The third side is known as the hypotenuse, and it is the longest of the three sides.
The square of the hypotenuse of a right triangle is equal to the sum of the squares of the remaining two legs, according to Pythagoras’ theorem. The right triangle formula can be expressed using this rule as follows: The hypotenuse square is equal to the sum of the base square and the altitude square.

Hypotenuse² = Base² + Perpendicular²

What are Pythagorean Triplets? The Pythagorean triplets are the three numbers that satisfy the preceding equation. (3, 4, 5) is a Pythagorean triplet, for example. Some additional instances of Pythagorean triples include (6, 8, 10), and (12, 5, 13).

Properties of Right Angle Triangle

The characteristics of a right angle triangle are discussed below.

One of the angles is always 90° or the correct angle.
The other two angles are acute angles because they are less than 90o.
The total of the remaining two inner angles equals 90°.
The other two sides adjacent to the right angle are named base and perpendicular.
The side in the right triangle opposite angle of 90° is the hypotenuse.
The longest side is always the hypotenuse.
We get three similar triangles if we drop a perpendicular from the right angle to the hypotenuse.
The side measurements adhere to Pythagoras’ rule.
If we draw a circumcircle through all three vertices, the radius of that circle is half the length of the hypotenuse.
It cannot possess any obtuse angles (angles bigger than 90° but less than 180° are considered obtuse).

Right Angle Triangle Area

The area of a right angle triangle is an area filled by the triangle’s borders or perimeter.

The right angle triangle is exactly half of the product of the triangle’s base and height.
Because it is a two-dimensional variable, it is expressed in square units. It is computed in square units. The area is usually represented by the units m², cm², in², yd², and others.
The base and height are the two sides necessary to calculate the right triangle area.

How to Determine the Area of a Right Angle Triangle –
The area of a triangle is computed by dividing the product of its base and height by half.

The following formula shows the area of a right triangle.

⇒Area of a right angle triangle = (1/2 × base × height) square units.

Right Angle Triangle Perimeter Formula

A right angle triangle perimeter is the sum of its three sides’ dimensions. The three sides of a right triangle are known as the Base, Perpendicular, and Hypotenuse. As a result, The perimeter of a right triangle is equal to the sum of its base, height, and hypotenuse.

Right triangle perimeter formula = length of (base + perpendicular + hypotenuse)

If the sides of a right triangle are a, b, c. Then the perimeter of the right triangle equals the total of its sides.

As a result, perimeter = (a + b + c) unit of length

Example – Q. In a right-angle triangle, the base is 4cm, the perpendicular is 3cm, and the hypotenuse is 5cm. What is the area of a right triangle?

Answer – The right triangle perimeter is = 4 + 3 + 5 = 12 cm

Things to Remember about right triangle

Some of the most crucial things that you need to remember about the right triangle are listed below.

The Pythagorean theorem is always satisfied by the side lengths of a right-angled triangle.
The area of a right triangle is computed as the Area of a right triangle = 1/2 base height.
The hypotenuse is the longest side of a right triangle and is the side opposite the right angle.
(Hypotenuse)2 = (Base)2 + (Altitude)2 ( in a right triangle).
The other two legs are perpendicular; one is the base and the other is the height.
Angles in isosceles right triangles are 90º, 45º, 45º.
A right triangle’s perimeter is the sum of the lengths of its three sides.