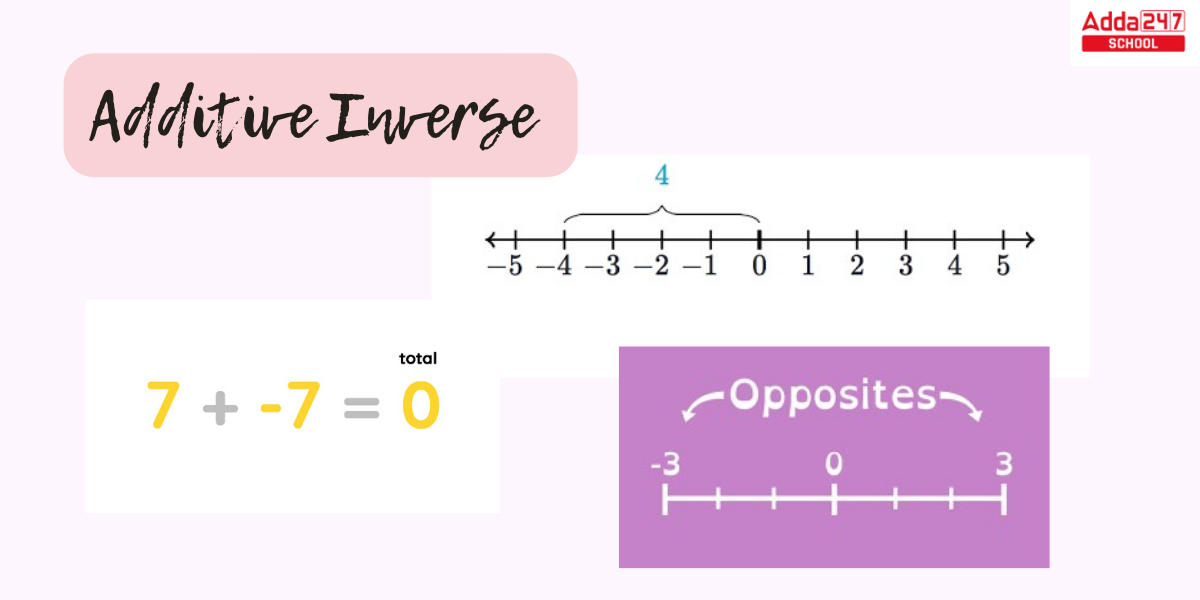
Additive Inverse: Each integer/ number has an additive inverse that is distinct from the inverses of the other numbers. The additive inverse of a number is the number that results in zero when added to the original number. In other words, the two numbers cancel each other out when it comes to adding. Every real number has a distinct additive inverse. For example, if a number is 10, its additive inverse is -10 because the addition of 10 and -10 equals zero. As a result, Additive Inverse is similar to the phenomena in which a positive and a negative charge cancel each other out.
Additive Inverse
What is Additive Inverse? Additive Inverse is the inverse of a number that, when added to the number, results in a sum of zero. It simply implies converting a positive number to a negative number and a negative number to a positive number because the sum of a positive number and its negative equivalent equals zero. We already know that 6+ (-6) equals 0. As a result, -6 is the additive inverse of 6 and -6 is the additive inverse of 6. This post discusses into the notion of Additive Inverse, including how to calculate the additive inverse of a number, characteristics, the additive inverse formula, and a lot more.
Additive Inverse Examples
A number’s additive inverse is its opposite number. Additive inverse is also a negation of a number or a changed sign of the original number. When a number adds up to its additive inverse, the sum of both numbers equals zero. The simple rule is to transform the positive integer to a negative number and vice versa.
- Additive Inverse Examples –
- The additive inverse of 8 is -8, as 8 + (-8) = 0.
- The additive inverse of -4 is 4, as (-4) + 4 = 0.
What is Additive Inverse Characteristics
Characteristics of Additive Inverse are mentioned below.
- When the sum of two real numbers is zero, one of them is considered to be the additive inverse of the other. If a + b = 0, and a and b are real numbers, then an is the additive inverse of b and b is the additive inverse of a.
- Based on the negation of the original number, the features of the additive inverse are given below. If x is the original number, then the additive inverse is -x. So, we’ll look at the features of -x here.
- −(−a) = a
- (-a)2 = a2
- −(a + b) = (−a) + (−b)
- −(a – b) = a − b
- a − (−b) = a + b
- (−a) × b = a × (−b) = −(a × b)
- (−a) × (−b) = a × b
How to calculate Additive Inverse?
Several methods exist for determining the additive inverse of an integer.
Method 1: Subtraction technique
Allow ‘A’ to be any actual number. Simply subtract ‘A’ from 0 to discover the additive inverse of A.
additive inverse ⇒ 0 -A = -A
Examples:
10’s additive inverse is 0 – 10 = – 10
– 3’s additive inverse is 0 – (-3) = +3
Method 2: Changing the sign
To find the additive inverse of any given number, change its sign. A positive number’s additive inverse is negative, whereas a negative number’s additive inverse is positive. Except for the sign, there will be no change in the numerical value.
The additive inverse of 5 is, for example, -5, whereas the additive inverse of -8 is 8.
Method 3: multiplication method
Allow p to be any actual number. Simply multiply p by -1 to discover the additive inverse of p.
p’s additive inverse = (- 1) p
Examples:
(-7) is the additive inverse of ⇒ 7.
-81’s additive inverse = (- 1) (- 81) = 81
Additive Inverse Formula
Additive inverse formula 1 –
Using the methods given above, we can derive the Additive inverse formula.
To calculate the additive inverse of x, subtract it from 0.
additive Inverse formula, x = 0 – x
Additive Inverse Formula 2 –
To obtain the additive inverse, multiply the provided integer by -1.
The additive inverse of p is, p(- 1) = -p
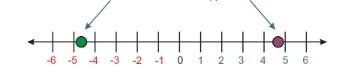
Additive Inverse in Number Line
The additive inverse in Number Line is a particular number, every real number has one. These inverses are found in pairs. In other terms, 0 is the midway of a number line segment connecting the supplied number and its additive inverse.
We may simply find the additive inverse of a number on a number line. Take note of the provided number’s distance from the origin. Mark the opposite direction of 0 which is the same distance away.
Here in this image, we can see the additive inverse of ‘5’ is ‘-5’. the additive inverse of ‘5’ is sitting on the opposite side and it covers the same distance from ‘0’ on the number line.
Additive Inverse of Whole Numbers
Natural numbers are counting numbers that are specified by the set 1, 2, 3, 4, 5, 6, 7, 8, 9, 10……n. Positive numbers are found throughout nature. Positive numbers are also whole numbers excluding 0. As a result, the additive inverse of any natural or whole integer except 0 is always negative.
- Examples:
- The additive inverse of 0 is 0.
- The additive inverse of 2 is -2.
- -465 is the additive inverse of 465.
Additive Inverse of Rational Numbers
Rational numbers have the form a/b, where a and b are integers and b is greater than zero. -a/b is the additive inverse of a rational number a/b.
For example,
- the additive inverse of 3/8 is -3/8.
- -2/3 is the additive inverse of 2/3.
- The additive inverse of 9/12 is -9/12.
Additive Inverse of Fractions
A fraction is a number denoted by the symbol a/b, where a and b are whole numbers and y is not equal to zero.
-
is the additive inverse of a fraction
.
- Examples:
- The additive inverse of 3/4 is
.
- The additive inverse of
is
.
- The additive inverse of 3/4 is
Additive Inverse of Decimal
We’ve seen how an additive inverse is applied to a value to make it zero. Let’s see how easy it is to find the additive inverse of decimals. The additive inverse of any decimal that is ‘a’ is ‘-a’.
- Example –
- The additive inverse of 0.13, is -0.13, where 0.13 + (- 0.13) = 0.
- The additive inverse of 2.23, is -2.23, where 2.23 + (- 2.23) = 0.
Additive Inverse of Complex Number
A complex number is an ordered pair of numbers (p, q) expressed in the form p + iq, where p is the real number and q is the imaginary number.
-(4 + 2i) is the additive inverse of 4 + 2i, -(b – 2i) is the additive inverse of b – 2i, and so on.
Now, the additive inverse of p + iq should be a value such that when added to a given complex number, the result is zero. As a result, it will be -(p + iq).
For example, the additive inverse of 6 + 3i is -(6+3i).
6 + 3i + [-(6 + 3i)]
= 6+3i -6-3i
= 0
Additive Inverse in Algebra
Sign change or negation is the operation of converting a number to its additive inverse. The additive inverse property can be extended to algebraic equations. The additive inverse of an algebraic expression is one that makes the total of all the terms zero, following the same rule as mentioned above for different types of integers.
For example, The additive inverse of the expression – B is -(B).
The additive inverse of x3 + 4 is – (x3 + 4) = -x3 – 4.
The additive inverse of x + 5y is -x – 3y, which results in the sum of all the elements being zero.
Additive Inverse vs. Multiplicative Inverse
The differences Between Additive Inverse and Multiplicative are shown in the table below.
| Difference Between Additive Inverse and Multiplicative | |
| Additive Inverse |
Multiplicative Inverse
|
| When the additive inverse is applied to the original integer, the sum is 0. | A multiplicative inverse is a number whose result is 1 when multiplied by the original number. |
| The additive inverse of a number is its negative or opposite. | The reciprocal of a number is the multiplicative inverse of that number. |
| A number’s sum and the additive inverse are always 0. | A number’s product with its multiplicative inverse is always 1. |
| The additive inverse of 0 is zero. | There is no multiplicative inverse for 0. |
| The original number’s sign is modified and appended. | The original number is multiplied by its reciprocal. |
| The additive inverse of any real integer a is -a. | The additive multiplicative inverse of any non-zero real number n is 1/a. |
| For example, 50 + (-50) = 0. | For instance, 50 (1/50) = 1 |
Additive Inverse of 0
The additive inverse of a number is another number that, when added to the original number, equals zero. In the case of 0, its additive inverse is also 0.
So, the additive inverse of 0 is 0:
0 + 0 = 0
Additive Inverse of 2
The additive inverse of a number is the value that, when added to the original number, equals zero.
In this case, the additive inverse of 2 is -2, because:
2 + (-2) = 0
Additive Inverse of 3
The additive inverse of a number is another number that, when added to the original number, results in a sum of zero. In the case of the number 3, its additive inverse is -3, because:
3 + (-3) = 0
So, the additive inverse of 3 is -3.
Additive Inverse of 5
The additive inverse of a number is the number that, when added to it, results in zero. For the number 5, its additive inverse is -5 because:
5 + (-5) = 0








 HPBOSE Compartment Date Sheet 2025 Out, ...
HPBOSE Compartment Date Sheet 2025 Out, ...
 RUHS Counselling 2025 Round 1 Seat Allot...
RUHS Counselling 2025 Round 1 Seat Allot...
 Bihar Board Dummy Registration Card 2026...
Bihar Board Dummy Registration Card 2026...










