Diagonals
In geometry, a diagonal is a line segment that connects two vertices of a polygon or solid that are not on the same edge. In general, a diagonal is defined as a slanted line that connects the vertices of a shape. We can find the diagonals of curved forms like circles, spheres, cones, and so on. Let us explore the significance of the diagonal line, as well as diagonal examples for various polygons such as square, rectangle, rhombus, parallelogram, and so on, along with their formulas, in this article.
Meaning of Diagonal in Maths
The term diagonal comes from the Greek word “diagonios,” which means “from one angle to another.” A diagonal in maths, as the name implies, is a straight line that connects the opposite corners of a polygon or polyhedron through its vertex. In addition, the diagonal of a square matrix defines the set of entities from one corner to the farthest corner in matrix algebra.
What are Diagonals?
A diagonal in geometry is defined as a line segment that connects two opposed vertices or corners of a polygon. A diagonal, in other terms, is a straight line that connects the opposite corners of a polygon or polyhedron via its vertex. It connects the vertices of a polygon but does not include the figure’s edges.
Diagonal Shape
A diagonal is described in mathematics as a sloping line or a slant line that links to the vertices of a polygon or a solid whose vertices are not on the same edge. A diagonal has the geometry of a straight line because it is a line segment connecting non-adjacent vertices or corners. The length of the polygon’s diagonal is always bigger than the length of the polygon’s sides. A polygon can have more than one diagonal, and the number of diagonals depends on the number of sides. The simplest polygon with a diagonal is the quadrilateral, which has two diagonals.
Diagonal Examples
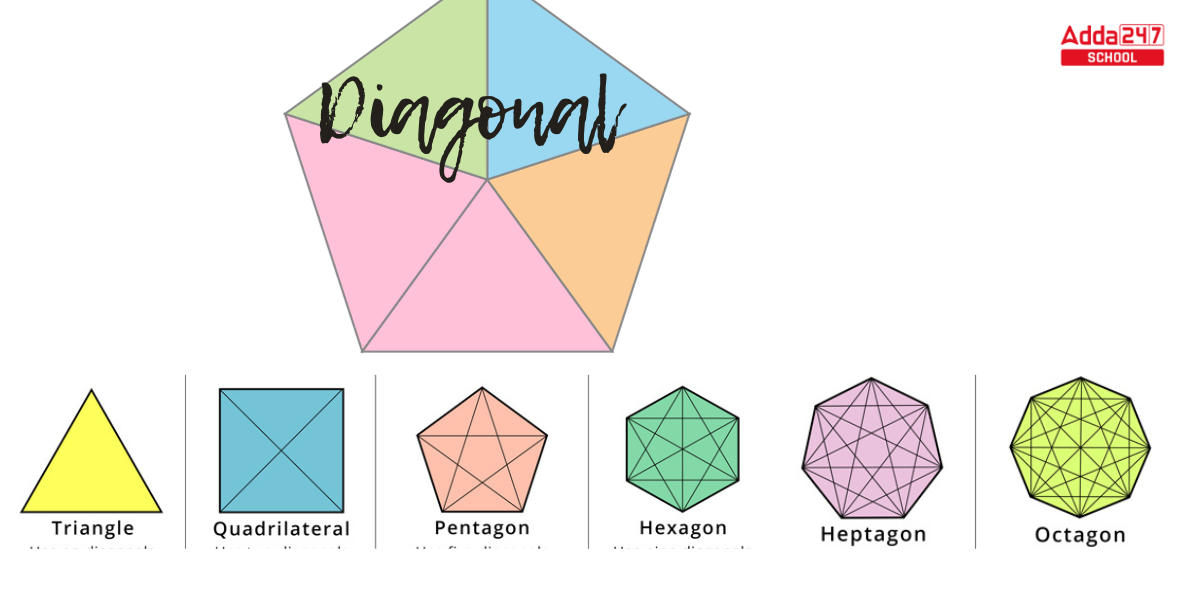
Diagonals are defined only for lateral shapes, or shapes with corners, such as Squares, Rectangles, Pentagons, and so on, but not for curved shapes like Circles and others. A diagonal can also be established for 3-D shapes like Cubes, Cuboids, and so on. The graphic below depicts a square with the square having two diagonals,
The diagonals of the above-mentioned ABCD square are AC and AC.
Diagonals Formula
The number of diagonals in a polygon varies depending on its kind and the number of sides. If “n” is the number of vertices in a polygon, the number of diagonals in a polygon may be calculated using the following formula:
The number of diagonals in a polygon with “n” vertices = [n(n-3)]/2
Consider the following square. There are four vertices in a square. Apply the above formula to get the number of diagonals in a square.
Number of square diagonals = 4(4-3)/2 = 4(1)/2 = 2
As a result, the square has two diagonals
Number of Diagonals of Shapes
The number of diagonals of some polygons determined using this algorithm is shown in the table below.
| Shape | Number of sides (n) | Number of Diagonals |
| Triangle | 3 | 3(3 – 3)/2 = 0 |
| Quadrilateral | 4 | 4(4 – 3)/2 = 2 |
| Pentagon | 5 | 5(5 – 3)/2 = 5 |
| Hexagon | 6 | 6(6 – 3)/2 = 9 |
| Heptagon | 7 | 7(7 – 3)/2 = 14 |
| Octagon | 8 | 8(8 – 3)/2 = 20 |
| Nonagon | 9 | 9(9 – 3)/2 = 27 |
| Decagon | 10 | 10(10 – 3)/2 = 35 |
| Hendecagon | 11 | 11(11 – 3)/2 = 44 |
| Dodecagon | 12 | 12(12 – 3)/2 = 54 |
Diagonals of Polygons
The diagonal of a polygon is a line segment that links any two non-adjacent vertices. A polygon is a two-dimensional closed object with straight sides that is flat or plane. Depending on the type of polygon and the number of sides, The number of diagonals in each polygon may vary. Let’s learn more about the diagonals of polygons along with formulas now.
- Diagonals of Triangle
- Diagonals of Square
- Diagonals of Rectangle
- Diagonals of Rhombus
- Diagonals of Parallelogram
- Diagonals of Pentagon
- Diagonals of Hexagon
Diagonals of Triangle
A triangle is defined by its three sides, three angles, and three vertices. A triangle lacked any diagonals since it lacked any non-adjacent vertices. It signifies that no line segments can be used to build diagonals. As a result, the number of diagonals in a triangle equals zero. In other words, a triangle has no diagonals.
The number of diagonals for a triangle = 0
Diagonals of Square
A square is a two-dimensional closed form with four sides and four corners. The opposing sides are parallel, and all of the sides are the same length. A square’s diagonals are the line segments that connect the square’s opposite vertices. There are two diagonals in a square. The square’s two diagonals are congruent to each other. The square’s diagonals are also bisected. A square’s diagonal divides it into two equal right triangles, with the diagonal becoming the hypotenuse of the right-angled triangles formed, as seen below.
The number of diagonals of square = 2.
The formula for calculating the length of a diagonal of a Square = a√2
Where “a” is the length of any square side.
Diagonals of Rectangle
A rectangle has two diagonals since it has four sides. A rectangle’s diagonal is a line segment that connects any two of its non-adjacent vertices. The diagonals of a rectangle are congruent and bisect one another. A diagonal divides a rectangle into two right triangles, and the diagonals become the hypotenuses of these triangles.
The number of diagonals of the rectangle = 2
The formula to find the length of Diagonal of a Rectangle is = √[l2 + b2]
Where “l” and “b” represent the rectangle’s length and width, respectively.
Diagonals of Rhombus
A rhombus is a quadrilateral with all four sides equal, however, all four angles are not equal in the case of the Rhombus. The diagonals of a rhombus are the line segments that connect the opposite vertices and bisect them at a 90° angle. The diagonal lengths are not equal because the rhombus’s four angles are not equal.
The number of diagonals for a Rhombus = 2
The length of diagonals formula is derived from the the area of the rhombus formula.
Area of a rhombus, A = (½) pq square units Where “p” and “q” are the length of two diagonals of the rhombus.
As a result, the formula for determining the length of the rhombus’ diagonal is:
Diagonal of a Rhombus, p = 2(A)/q and q = 2(A)/p
Diagonals of Parallelogram
A parallelogram is a quadrilateral with opposite sides and angles that are congruent. A rhombus has four sides, and its two diagonals intersect at right angles, as seen in the diagram below.
Diagonals of Trapezium
The Trapezium is a quadrilateral with two parallel sides. It only contains two parallel lines, and the other pair is not parallel. A trapezium has two diagonals; the graphic below displays a trapezium ABCD, with AC as the diagonal.
Diagonals of Pentagon
A pentagon is a two-dimensional shape with five sides and five vertices. All five sides of a normal pentagon are equal, and we may conclude that a pentagon has 5 diagonals using the diagonal formula. In the case of a regular pentagon, all five diagonals are the same. The illustration below depicts a pentagon and all of its diagonals.
Diagonals of pentagon = 5
Diagonals of Hexagoan
A pentagon is a two-dimensional closed figure with five vertices. When the non-adjacent corners are brought together, it forms a polygon with nine diagonals. The diagonal of the pentagon is depicted in the image below.
Diagonals of Hexagon = 9
Diagonals of 3D shapes
3D shapes, like polygons, have diagonals. They have body diagonals (space diagonals) and face diagonals because they are three-dimensional figures. The (body)diagonals in 3-D shapes are the lines that connect the non-planer vertices of the 3-D shape. The diagonal of 3-D objects like Cubes and Cubiods is explored further below.
Diagonals of Cube
A cube is a three-dimensional square solid with edges that are all the same length. This means that a cube’s length, breadth, and height are all the same, and all of its faces are squares. It is made up of 12 edges and 8 vertices.
The diagonals of the cube’s faces are straight lines that connect the opposite vertices on each face. A cube’s body diagonal is the line segment that runs through its center, connecting the opposite vertices. The diagonals of a Cube are shown in the below image.
Diagonals of a Cube:
- Number of primary diagonals of cube = 4
- Number of diagonals on the faces of the cube = 12
- Total diagonals of the cube = 12 + 4 = 16
Length of
If we have a cube with side “a,” the length of its face diagonal is computed using Pythagoras’ Theorem is as follows
Length of Face Diagonal = √2(a) units.
Also, for body diagonals, we utilize Pythagoras’ theorem twice, and the resulting formula for the length of the body diagonal is
Length of Body Diagonal = √(a) units.
Diagonals of Cuboid
A cuboid is a three-dimensional shape with six rectangular faces as well. It contains 12 edges and 8 vertices, the same as the cube.It is a three-dimensional representation of a rectangle. A cuboid’s diagonals are divided into two types: body diagonals and face diagonals. A cube’s body diagonal is the line segment that runs through the center and connects the opposite vertices. The face diagonal connects the opposite vertices on each face.
As the basic structure of the cube and cuboid is comparable, the number of diagonals in both shapes will be equal.
Diagonal of Cuboid Formula:
- Number of primary diagonals of cube = 4
- Number of diagonals on the faces of the cube = 12
- Total diagonals of the cube = 12 + 4 = 16
Diagonal of Cube Formula:
If we have a cuboid with sides “a,” “b,” and “c,” then its face diagonal along the face with dimensions a and b is determined using Pythagoras Theorem as,
Diagonal Face Length =√ (a²+ b²) units
We employ Pythagoras’ theorem twice for body diagonals, and the resulting formula for body diagonal length is,
Length of Body Diagonal of a cuboid = √(a²+ b² + c²) unit
Length of Diagonals
The length of a diagonal in any polygon is determined by the type of polygon. There is no generic formula for calculating the diagonal length. Rather, the formula for calculating the length of the diagonal can be determined from the measurements of the specific polygon. The length of diagonals of various shapes is determined by their dimensions.
| length of Diagonal | Formulas |
| Length of Diagonal of Square |
a√2
where a is the length of the side of the square |
| Length of Diagonal of Rectangle |
√(l2 + b2)
Where l and b are the length and breadth of the rectangle, respectively |
| Length of Diagonal of Cube |
a√3
Where a is the length of the edges of the cube |
| Length of Diagonal of Cuboid |
√(l2 + b2 + h2)
Where l, b, and h are the length, breadth, and height of a cuboid |








 NEET UG 2025 Counselling Dates OUT! Chec...
NEET UG 2025 Counselling Dates OUT! Chec...
 Dr MGR Medical University Results 2025 R...
Dr MGR Medical University Results 2025 R...
 GSEB HSC Science Supply Result 2025 Down...
GSEB HSC Science Supply Result 2025 Down...









