Obtuse Angle- Definition, Degree, Properties, and Examples

Obtuse angles are one of the six major types of angles present in geometry. It is an essential angle of the geometrical world whose presence is felt even in the real world. It is a unique angle that differs from the usual right angle. In geometry, an angle is a shape created by two rays that meet at a point known as a vertex. The two rays symbolize the two sides of the angle. Angles are formed in the plane when two curves touch. To discover the mysteries of angles greater than 90 degrees, let’s examine the definition, properties, and examples of these special angles.

Obtuse Angle

Obtuse angle is an angle whose measurement lies in the range of 90° to 180°. In other words, the value of this angle will always be more than 90° and will always be less than 180°. Any angle following this measurement criteria will be called an obtuse angle. Just like any other angle, these angles too exhibit some unique features and has real-life applications. These angles are not as sharp as acute angles, hence the name obtuse which means dull or not sharp. You can observe the formation of this angle in your wall clock in which the hour hand and the minute hand forms these angles during certain time intervals.

Obtuse Angle Definition

As per the formal mathematical definition, this angle is a special type of angle whose value is always greater than 90° and always less than 180°. In other words, an angle that lies between a right angle and a straight angle is obtuse in nature. That is, the value of this angle will always be more than 90° (right angle) and less than 180° (straight angle). The following figure will help you understand the shape of this special angle properly.

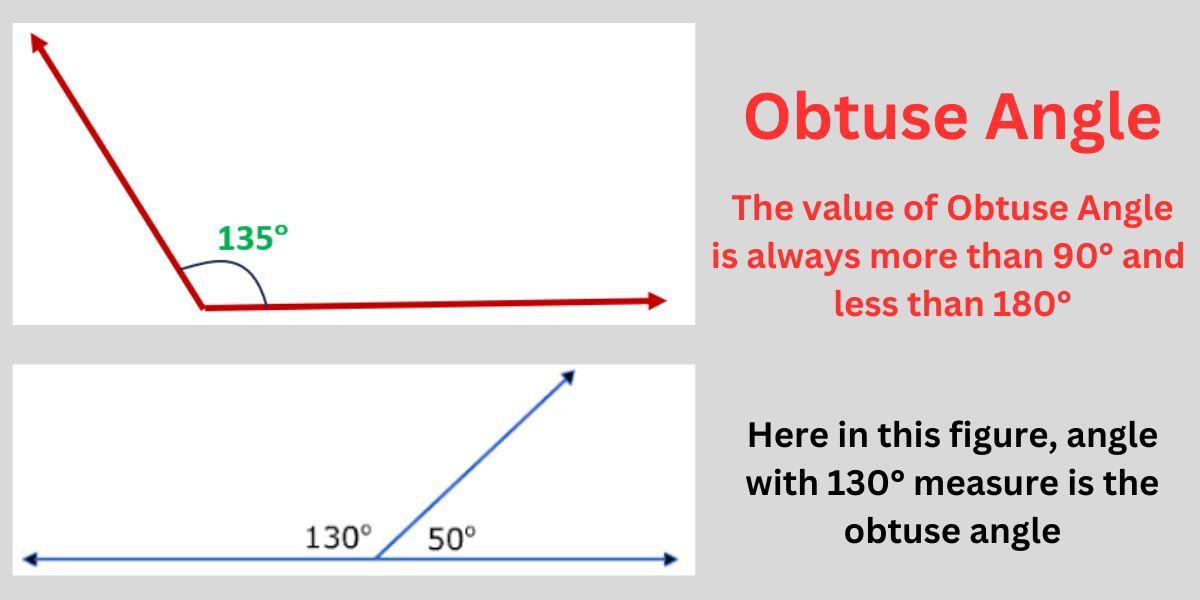
Obtuse Angle Degree

The degree value of this angle always oscillate between 90° and 180°. The value of this special angle can never be more than or equal to 180° and can never be less than or equal to 90°. Let us examine this concept through an example. Suppose there is an angle A. It is given that the angle is obtuse. Then angle A must satisfy the following criteria:

90° > A < 180°

Obtuse Angle Examples

Some of the examples of this angle are:

91°, 142°, 120°, 179°, 163°, 137°, 100°, etc.

Obtuse Angle Triangle

Obtuse Angle triangles are those triangles in which one angle is obtuse in nature, i.e., one angle measures more than 90°. It must be noted that such triangles can never be an equilateral triangle. It will always be either a scalene triangle or an isosceles triangle. The other two remaining angles of an such triangles are always acute angles. Similar to this, a triangle cannot have both a right angle and an angle that is obtuse in measurement. The following image will help you understand this special angle triangle in a proper way.

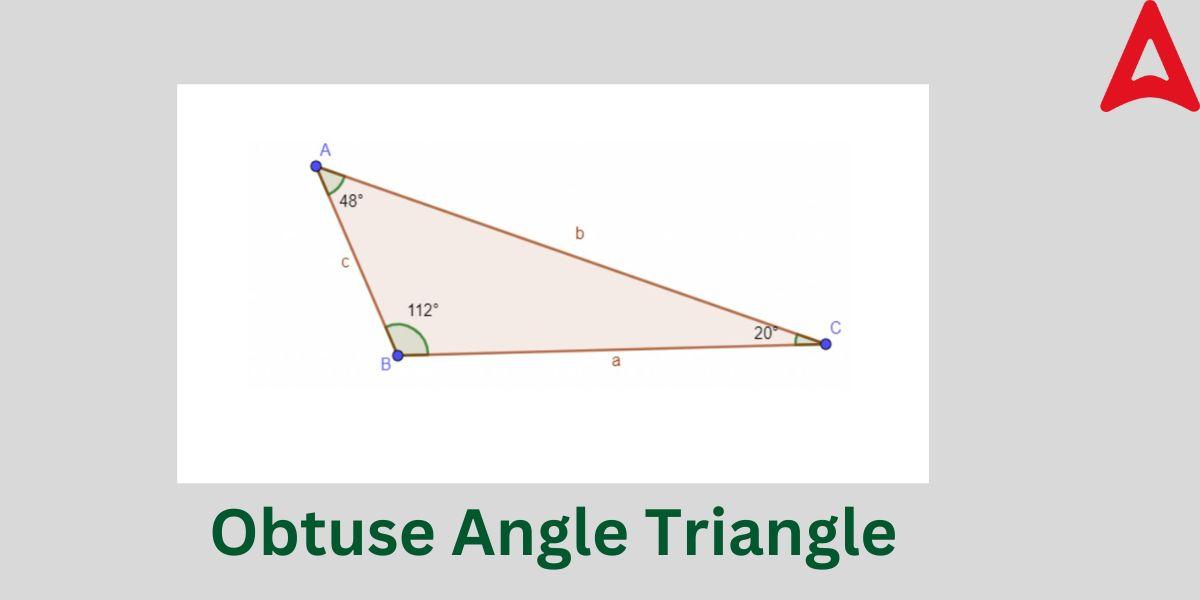
Obtuse Angle Properties

This special angle due to its uniqueness possess certain properties. These characteristics help students to identify and solve problems related to this angle. Some of the most important properties related to these angles are give below.

• The value of this angle is never more than 180° and never lesser than 90°
• In a full angle, if one angle is obtuse, then the other angle must be a reflexive angle.
• In a triangle, the side located opposite to the this angle is greatest of the three sides.
• In a triangle with an obtuse angle, the sum of squares of the largest side is always greater than the sum of squares of the two smaller sides
• A triangle cannot have more than 1 angle of obtuse nature

Obtuse Angle Real-Life Examples

These angles have made its presence felt in many different real world scenarios. Some of the real-life examples of these angles are:

• The angle between the hour hand and minute hand at 4 PM or AM
• The angle between the staircase and the upper floor
• The angle between the laptop screen and its base
• The angle between blades of a ceiling fan

Obtuse Angle Solved Examples

Some of the solved examples on this special angle given below will help students to understand this concept in a better way.

Example 1: If the value of an obtuse angle is 130°. Then what will be the value of its supplement?

Solution:  We have given the value of angle (obtuse) = 130°

As we know that supplementary angles sum equals 180°.

So, 130° + x = 180°, where x is the supplement of 130°

x = 180° – 130°

x = 50°

Example 2: In a triangle, the value of two acute angles are 30° and 42°. Find the value of the third angle of that triangle.

Solution: Given the value of two angles = 30° and 42°

As we know, sum of all the angles of a triangle = 180°

Let the value of the angle be x

so, 30° + 42° + x = 180°

72° + x = 180°

x = 180° – 72°

x = 108°

So the value of angle of the triangle = 108° (obtuse)

Example 3: What will the internal angle measure if the reflex angle of the provided rays is 260°? 

Solution: Given, reflex angle = 260°

We know that rays form a complete angle.

So, let the unknown angle be x

Hence, 260° + x = 360°

x = 120°

The unknown angle is a obtuse in nature with  a value of 120°.

Sharing is caring!