What is meant by arc length?

The arc length is the curved distance of a segment of the circle (known as arc). In other words, the distance along the curved line along a segment of the circle's circumference is known as arc length.

What is the arc length formula?

The arc length formula for an arc of length L is given by: L= (θ/360°)2Πr, when the angle is in degrees L= S = rθ, when the angle is in radians

What is central angle?

The angle subtended by the end points of the arc at the center of the circle is known as the central angle

Can the value of central angle be more than 360 degrees?

No, the value of the central angle can never be more than 360 degrees.

Arc Length Formula- Definition, Proof, Examples

Table of Contents

Arc Length Formula: The arc is a section of any length on the circumference (perimeter) of the circle. The arc length formula is an important formula related to the circumference of the circle which is used to calculate the arc length. Arc length is more accurately described as the length along the circumference of any circle or curve (arc). The arc length is the total length of the curved line that forms the arc. The arc length formula is used to obtain this length in different scenarios. Let us dive deep into this topic so that we can have a clear understanding of this particular domain of circle geometry.

Arc Length Formula

The arc length, which denotes the length of a curve or a segment of it, is a key idea in the study of curves. We may determine this distance precisely by using the arc length formula, which is a strong tool. We often use this formula in the case of circles, when we need to find the length of an arc segment, but this formula can be used for any arc (portion of the curve). In a circle, the arc’s length corresponds to a portion of the circle’s perimeter (circumference). The length of the arc will be determined by measuring the distance along the curved line that forms the arc.

Arc Length Formula Definition

As per the formal mathematical definition, the arc length formula is used to compute the curved line distance making up the arc (a segment of a circle). In other words, the formula for the arc length is used to calculate the curved distance of the arc from its one end to another. An arc is basically a segment of the circumference of the circle. To be more precise, the distance between the two locations along a segment of a curve is known as the arc length.

Arc Length Formula Degrees

To find out the arc length formula, we need to have a basic understanding of the concept of circle. As we know that, a full circle creates a 360° angle at the center. As arc is just a portion of the circle, so it subtend a certain angle which will be less than 360°. So by understanding this basic concept, we can now understand this formula using the figure given below.

In the above figure, L = arc length (which we want to find out)

θ = angle subtended by the end points of arc at the center (also known as the central angle) in degrees

r = radius of the circle

Using these quantities, the arc length formula is given by:

L = (θ/360°)2Πr

where Π = 22/7 or 3.14

It is to be noted that this formula holds true only if the value of angle is given in degrees.

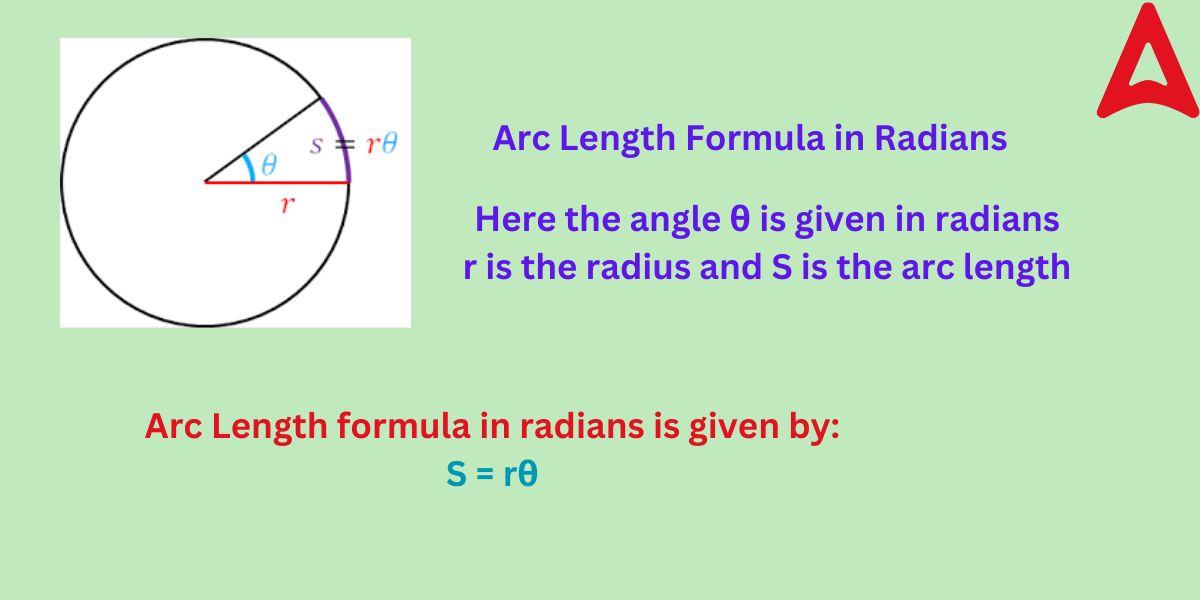
Arc Length Formula Radians

As we know that the value of angles can exist either in degrees of radians. The arc length formula can be used to derive the length of the arc both in degree and radian case. We already expressed the degree formula above. Let us now have a look at this formula in radians.

Let the central angle subtended by the two ends of arc be θ at the center

S be the arc length to be determined

r be the radius of the circle taken in to consideration

Then the arc length formula in radians will be:

S = rθ

This distance is also known as the length of an arc of a sector.

Arc Length Formula Integral

The arc length formula can also be expressed in the integral form. The formula in the integral form is given below.

\int_{m}^{n} {\sqrt{(1 +} d y / d x)}^{2} d x

where, m = starting point of the arc (lower limit)

n = end point of the arc (upper limit)

Arc Length Formula Proof

Just like any other mathematical equation, the arc length formula can be proved using fundamental mathematical concepts. The derivation or proof of the formula to find the arc length is very important from the examination point of view. Students from class 10 to class 12 are often asked in their examination to prove this formula. The proof for this formula is given below.

As we know that the angle subtended by the perimeter (circumference) of the circle at its center = 360°

Circle’s circumference, i.e., the length of the full arc = 2Πr, where r is circle’s radius

So, the length of an arc that subtends a unit degree at the center will be = 2Πr/360°

Let there be an arc of length L which subtends an angle θ at the center of the circle

So, the length L of the arc which subtends θ degree at the center will be:

L = (2Πr/360°) x θ

On rearranging it, we get:

L = (θ/360°)2Πr

Hence proved

Arc Length Formula Without Radius

Using the arc length formula, we can even find the length of the arc without knowing the value of the radius. It is one of the most useful feature which help students solve complex mathematical problems. To find the length of the arc without knowing the radius value, we need two quantities: central angle (θ) and sector area. The region inside the portion of the circle formed by two radii and an arc is known as the area of a sector. We can find the arc length using these two values in the following way.

As sector area is given by (θ/360°)Πr² ,if θ is in degree

or, Sector area = (1/2)r²θ, when θ is in radians

Using this, we can easily calculate the unknown value of r

After knowing the value of r, we can easily calculate the arc length using the formula for arc length

Arc Length Formula Properties

Some of the properties of the arc length formula that will help students in their academic journey is given below.

The arc length is always greater than the straight line or perpendicular distance between the two end points of an arc, which is also known as chord
This formula can be used to derive the value of arc length whether the angle value is in radians or degrees
The angle subtended by the arc length at the center is always less than 360°

Arc Length Formula Examples

Some of the solved questions given below will help students understand this crucial topic in a crystal clear manner. These solved examples will help readers in developing a solid foundation of the arc length formula.

Example 1: What will the length of the arc of a circle whose radius is 10 meter and the angle subtended by the arc at its center is 45°?

Solution: Given, radius (r) = 10 m

angle (θ) = 45°

As the angle is in degree

So using the arc length formula in degrees

arc length = (θ/360°)2Πr

arc length = (45/360) x 2 x 3.14 x 10

On solving, we get

arc length = 7.85 meter