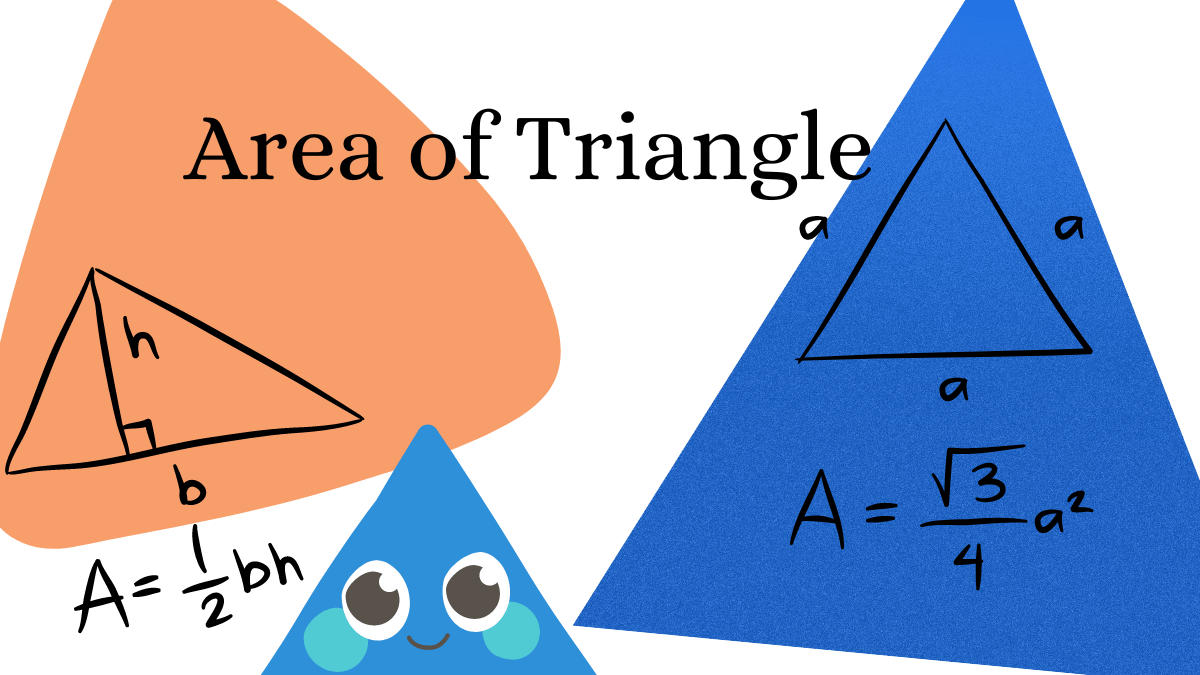
The “Area of Triangle” is a basic topic of geometry. The region enclosed by the three sides of any triangle is defined as the area of a triangle. In general, it is equal to half of the base times the height, i.e. A = 1/2 (bxh). As a result, to calculate the area of a triangular polygon, we must first find the base (b) and height (h). Area of Triangle applies to all forms of triangles, including scalene, isosceles, and equilateral triangles. Read the full article to learn how to get the area of a triangle.
Area of Triangle
In the Area of Triangle, it is observed that the triangle’s base and height are perpendicular to each other. The area unit is measured in square units (m2, cm2). In this article, we have discussed the area of the triangle and methods to calculate the area of a triangle. Stay tuned and read the entire article to learn how to calculate the area of a triangle and bookmark this page to get the latest updates of all the articles.
Area of Triangle Formula
There are many ways to calculate the Area of Triangle formula. For example, When we know two sides and the angle between them, we can use trigonometric functions to calculate the area of a triangle. The other method we can apply when we know the lengths of all three sides of a triangle, we can apply Heron’s formula to compute the area of a triangle. Furthermore, the basic formula for calculating the area of a triangle is:
| Area of Triangle = A = ½ (b × h) square units |
Here A = Area of Triangle
B = Base of Triangle
H = Height of a Triangle
Area of Triangle Formula Image
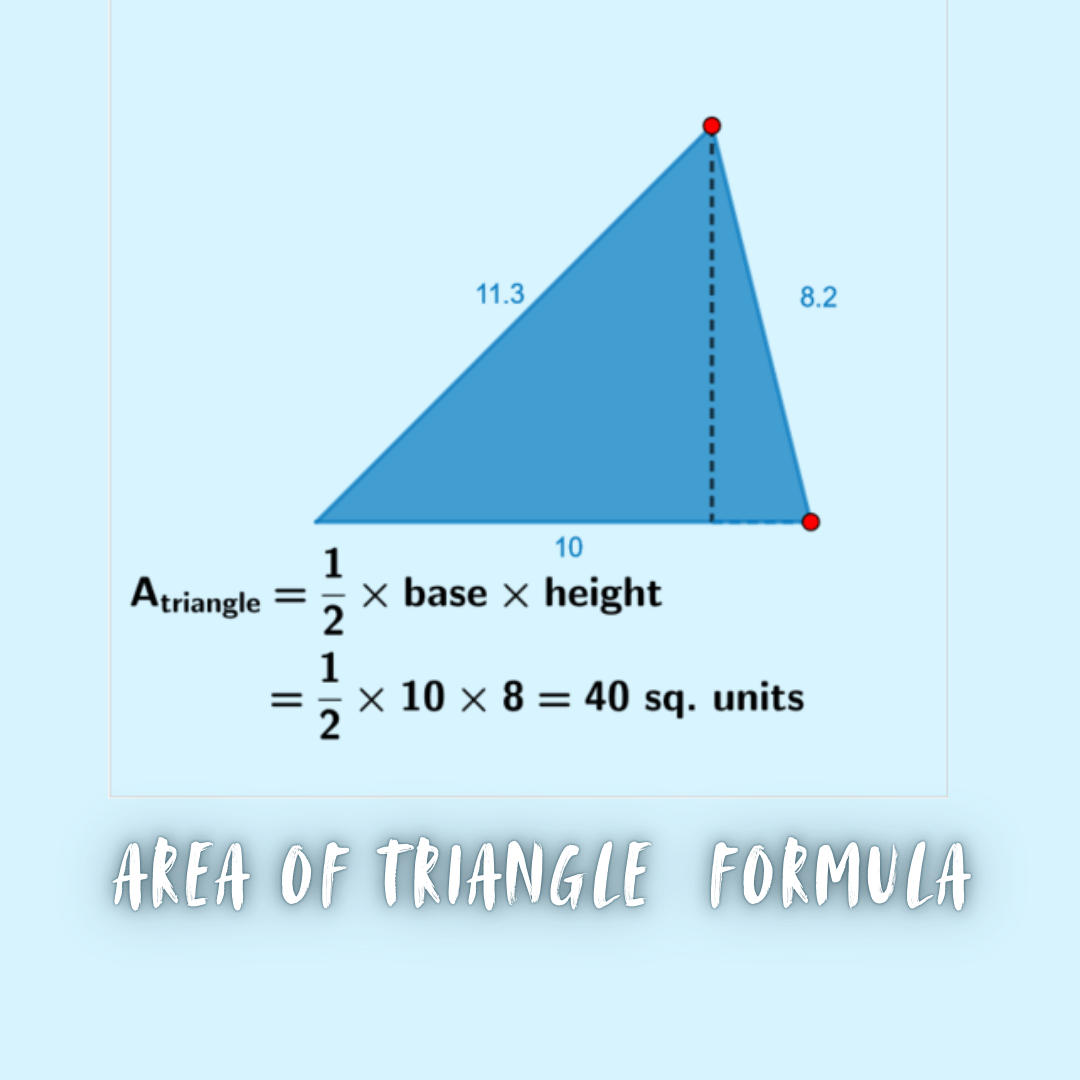
Area of Triangle in Co-ordinate Geometry
Here we have given the methods to calculate the Area of the Triangle using formulas. The formulas to calculate the area of different types of triangles like an isosceles triangle, equilateral triangle, and right-angled triangle are given below.
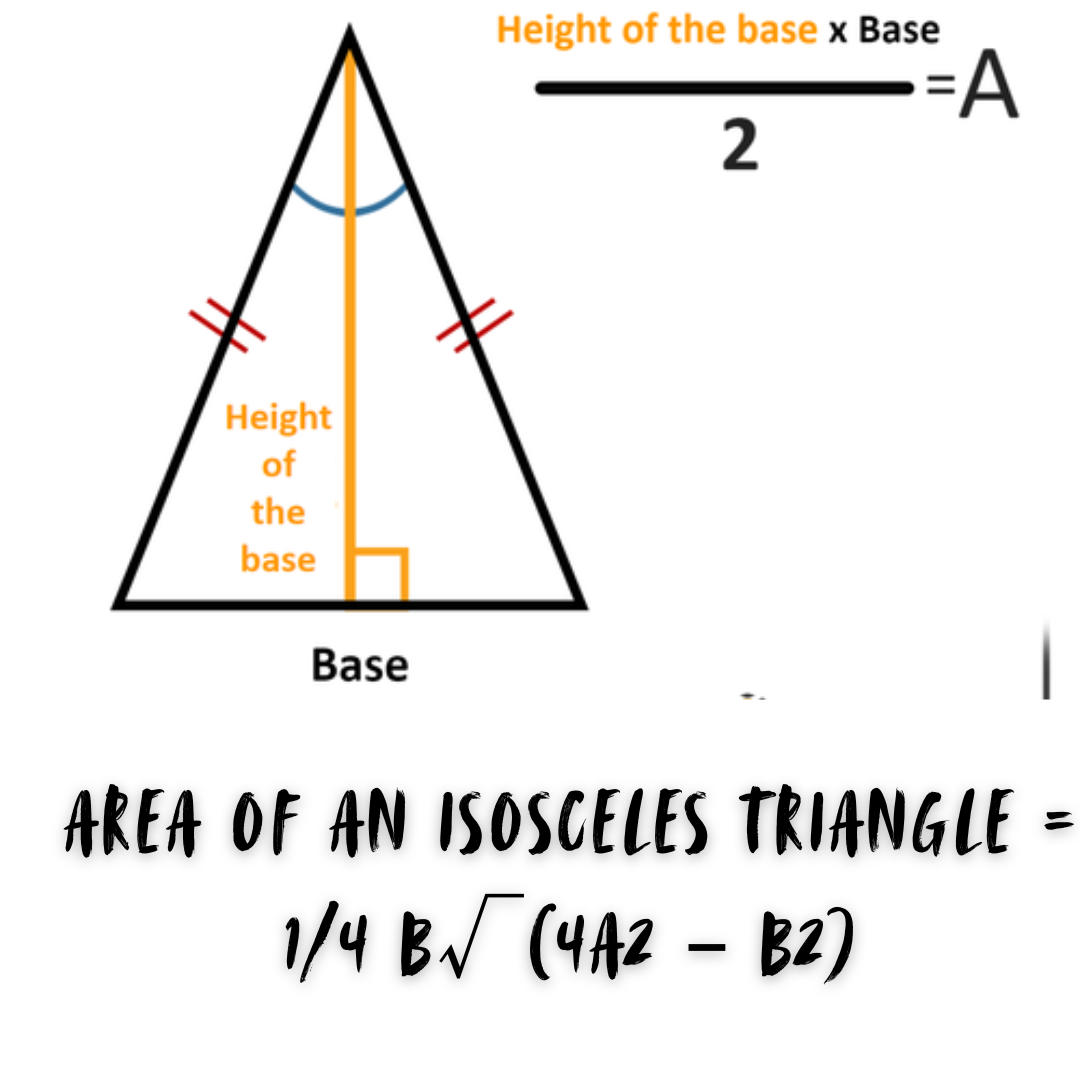
Area of an Isosceles Triangle
Two of the sides of an isosceles triangle are equal, and the angles opposite the equal sides are likewise equal.
| Area of an Isosceles Triangle = 1/4 b√(4a2 – b2) |
Where, b = Base of a Triangle
a = Measure of one of the sides from two equal sides
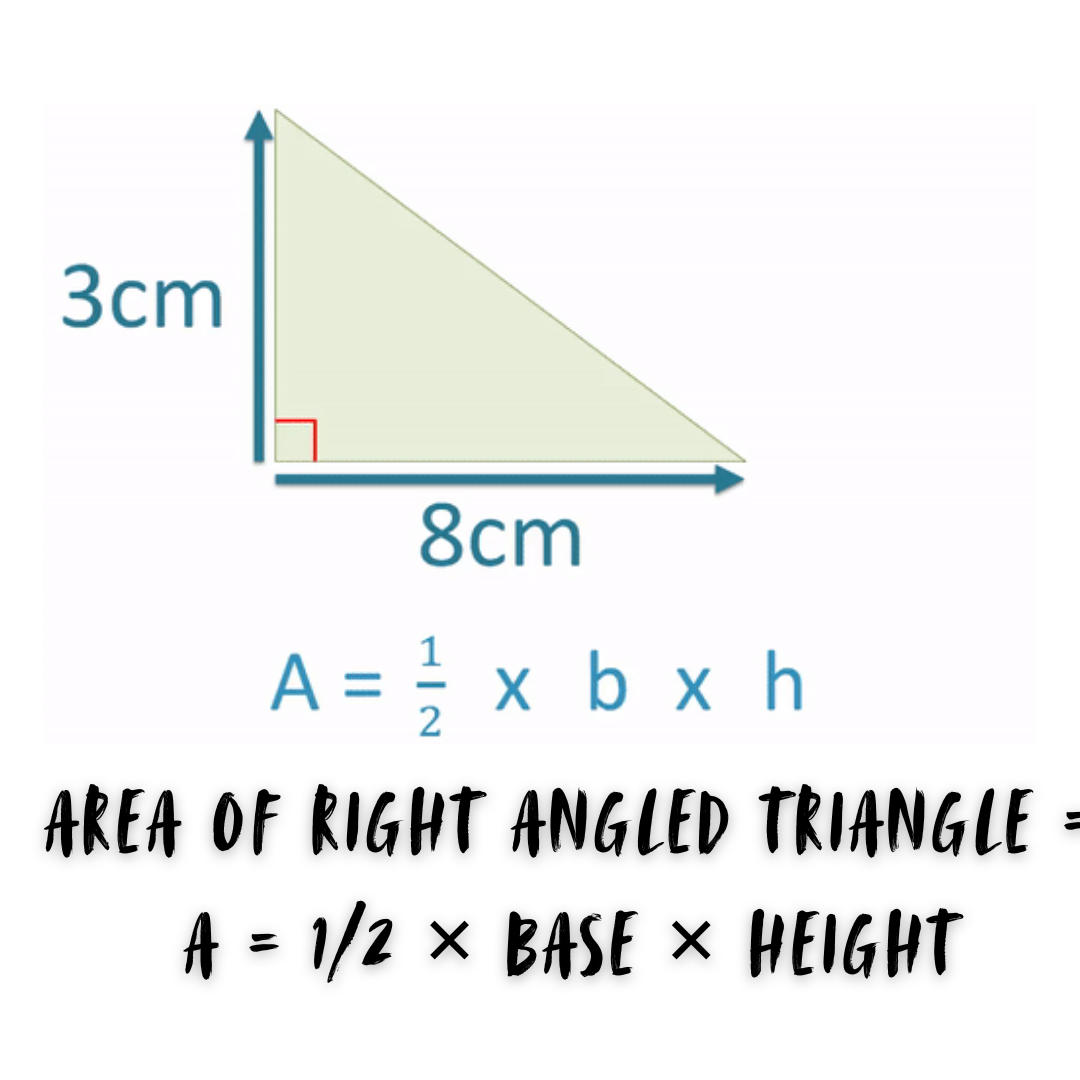
Area of Right Angled Triangle
A right-angled triangle, often known as a right triangle, has one 90° angle and two 60° angles that add up to 90°. As a result, the height of the triangle is equal to the length of the perpendicular side.
| Area of Right Angled Triangle = A = 1/2 × Base × Height |
Here A = Area of Triangle
B = Base of Triangle
H = Height of a Triangle
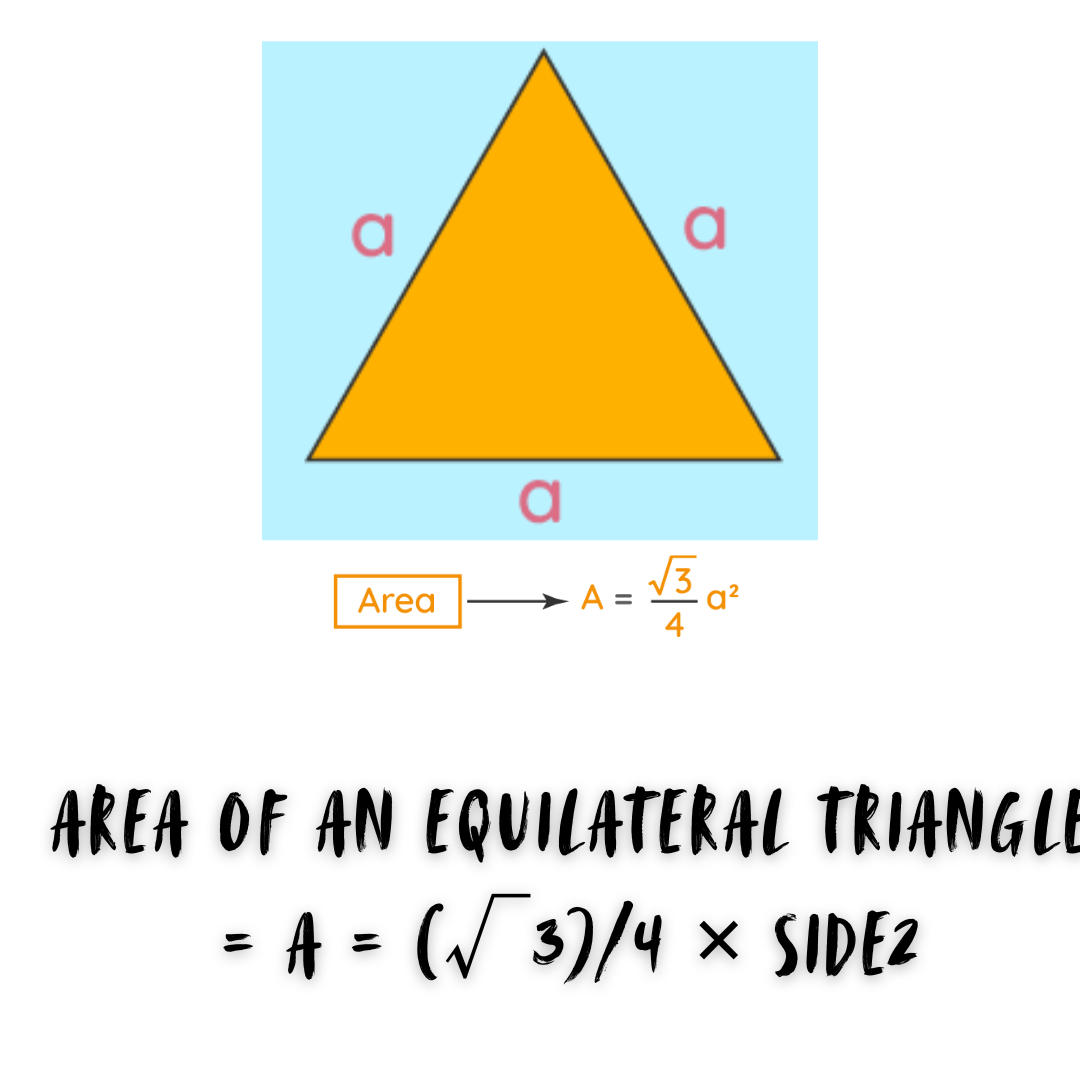
Area of an Equilateral Triangle (without Height)
An equilateral triangle is one with all of its sides equal. The perpendicular traced from the triangle’s vertex to its base divides the base into two equal pieces. To compute the area of an equilateral triangle, we must first determine the length of its sides.
| Area of an Equilateral Triangle = A = (√3)/4 × side2 |
Here, A = Area of Triangle
Side = side of the triangle
Area of Triangle using Heron’s formula
We can use Heron’s formula to calculate the area of a triangle if the lengths of its three sides are given. we must first determine the triangle’s perimeter, which is the distance covered by all three sides and is computed by combining their lengths.
Heron’s formula includes a few crucial steps.
- Calculate the semi-perimeter (half perimeter) of the specified triangle by adding all three sides and dividing by two.
- Enter the value of the triangle’s semi-perimeter into the primary formula, ‘Heron’s Formula’.
- Consider the triangle ABC, which has side lengths a, b, and c. To calculate the triangle’s area, we utilize Heron’s formula – Area = √s(s−a)(s−b)(s−c)
- The perimeter of the given triangle is (a + b + c). Therefore,’s’ is the semi-perimeter, which is (a + b + c)/2.
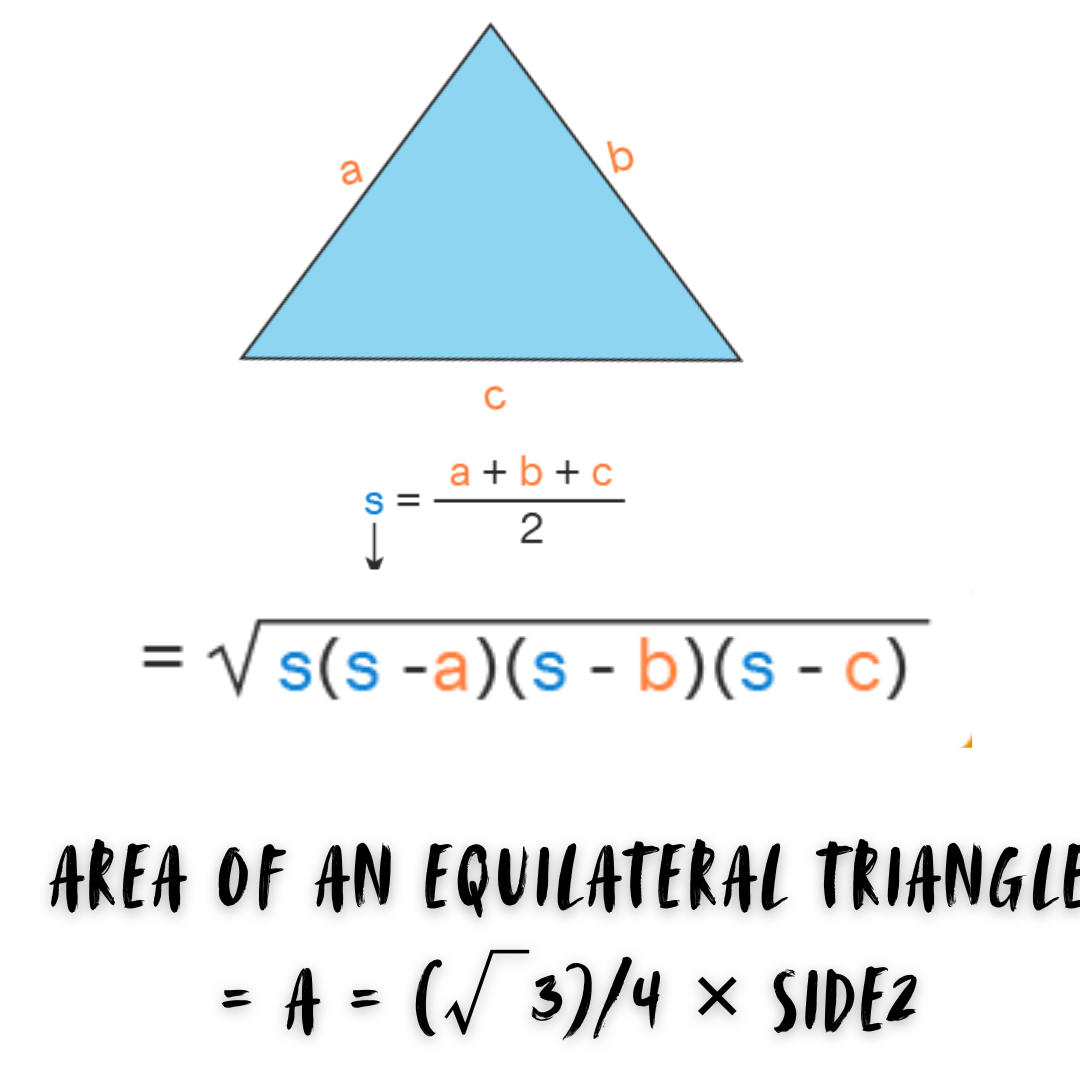
Area of Triangle Formula Table
Below we have given the Area of Triangle formulas to calculate the area of a triangle. Check out the table below:
| Particulars | Area of Triangle Formula |
| When a triangle’s base and height are known. | A = 1/2 (base × height) |
| When all the sides of a triangle are given like a, b, and c. | Heron’s formula
Area of a scalene triangle = √s(s−a)(s−b)(s−c) s = (a + b + c)/2 Where, a, b, and c = sides S = semi-perimeter of triangle |
| When an angle and two sides of a triangle are given | A = 1/2 × side 1 × side 2 × sin(θ)
Where, θ = Angle between the given two sides |
| When the height and base of the triangle are given. | Area of a right-angled triangle = 1/2 × Base × Height |
| In the case of an equilateral triangle | Area of an equilateral triangle = (√3)/4 × side2 |
| In the case of an isosceles triangle | Area of an isosceles triangle = 1/4 b√(4a2 – b2)
Where, b = base of the triangle the length of an equal side. |
Area of a Triangle with Two Sides and the Included Angle (SAS)
Now, in case you are given the two sides of a triangle and the angle between them, how can we calculate its area?
Solution – Consider the triangle ABC, with vertex angles ∠A, ∠B, and ∠C, and sides a, b, and c (image).
If any two sides and the angle between them are supplied, then the formulas to determine the area of a triangle are as follows:
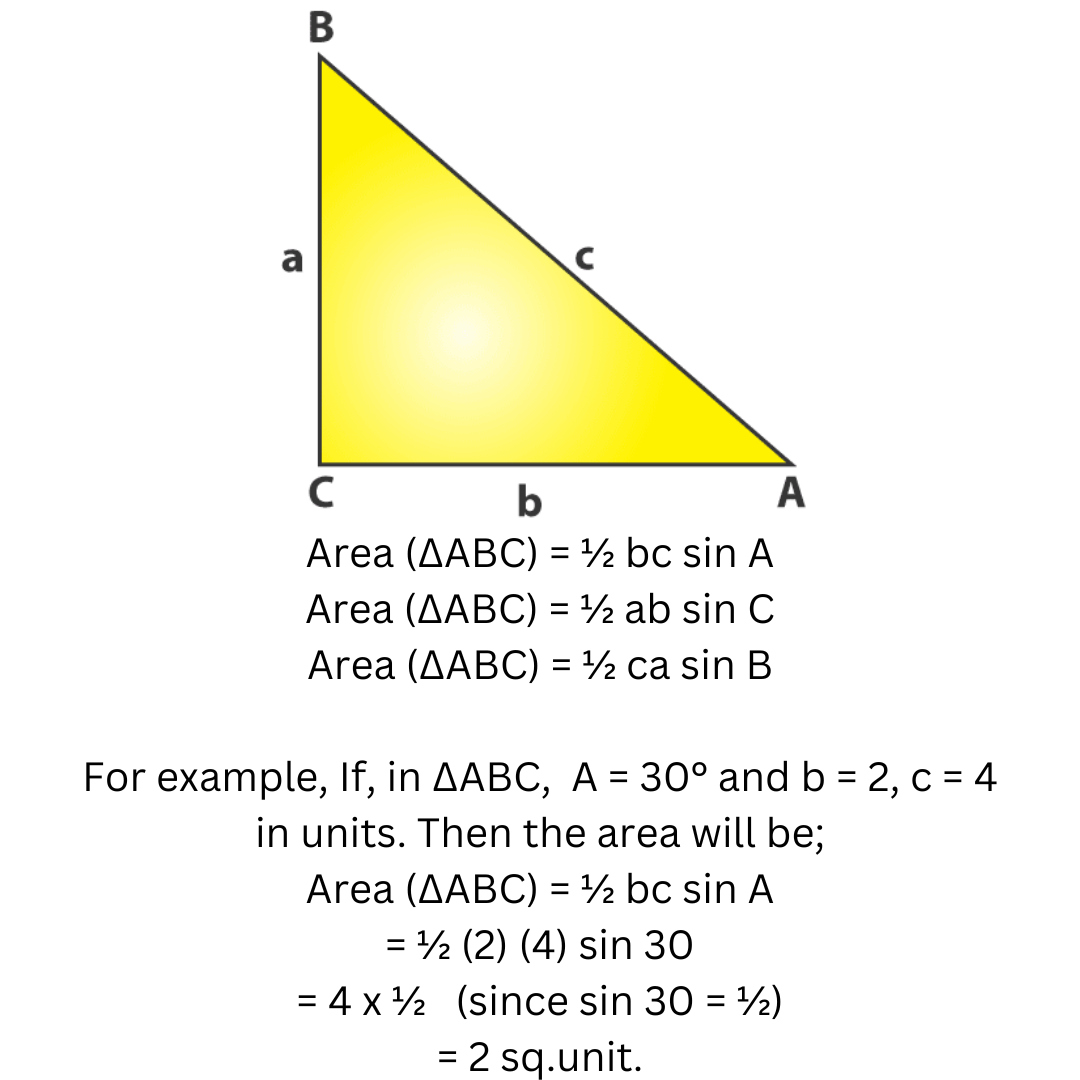
Area of a triangle under SAS
Area of Triangle Formula Solved Examples
Area of Triangle Some solved examples are given below.
Q.1: Find the area of a triangle with a base of 20 cm and a height of 10 cm.
Area of triangle = (1/2) × b × h
A = 1/2 × 20 × 10
A = 1/2 × 200
Thus, the area of a triangle is 100 cm2.
Q.2: Find the area of a triangle with a base of 6 cm and a height of 3 cm.
Area of triangle = (1/2) × b × h
A = 1/2 × 6×3
A = 1/2 ×18
Thus, the area of a triangle is 9 cm2.
Q.3: Find the area of a triangle with a base of 12 cm and a height of 16 cm.
Area of triangle = (1/2) × b × h
A = 1/2 × 12 × 16
A = 96
Thus, the area of triangle is 96 cm2.
Q.4: Find the area of an equilateral triangle with a side of 12 cm.
Area of an Equilateral Triangle = A = (√3)/4 × (side)2
Given the side of equilateral triangle = 12cm
A = (√3)/4 × (side)2
A = (√3)/4 × (12)2
A = (√3)/4 × 144
A = 36√3 cm2
| Related Articles | |
| Right Angle Triangle | Types of Triangle |
| Simple Interest Formula | Compound Interest Formula |








 Try CUET College Predictor 2025 to Predi...
Try CUET College Predictor 2025 to Predi...
 CUET Result 2025 OUT (Today) @cuet.nta.n...
CUET Result 2025 OUT (Today) @cuet.nta.n...
 Why the Delay in CUET UG 2025 Results? C...
Why the Delay in CUET UG 2025 Results? C...









