Isosceles Triangle- Definition, Properties, Angles, Formula & Types

Isosceles Triangle: In the study of geometry, An isosceles triangle is a triangle with two sides that are the same length. An isosceles triangle has two angles that are equal in size and opposite from equal sides. In this article, we will look at the definition of an isosceles triangle, its properties, and several isosceles triangle formulas.

Isosceles Triangle Definition

A triangle is a closed two-dimensional figure with three sides, three vertices, and three angles.
Triangles are three-sided polygons that are classed as equilateral, isosceles, or scalene depending on the length of their sides. If any two of them are equal, we call this an Isosceles triangle. As a result, if a triangle has two equal sides and two equal angles, it is an isosceles triangle.

What is Isosceles Triangle?

An isosceles triangle is a triangle having two equal sides. Furthermore, the angles opposing an isosceles triangle’s equal sides are equal. In other words, An isosceles triangle is a triangle with two congruent sides.

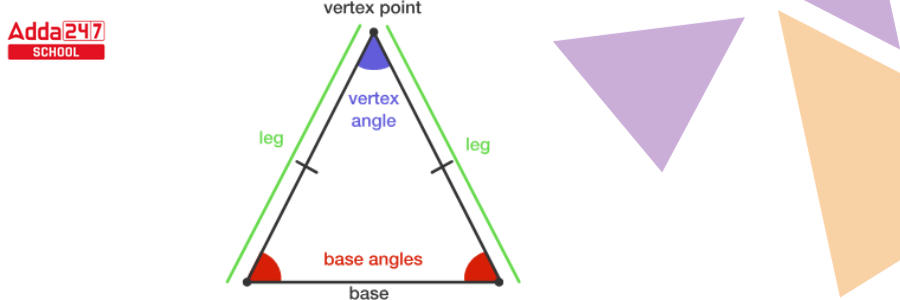
Figure of Isosceles Triangle

In the diagram below, ABC is an isosceles triangle with equal sides AC and BC. The angles opposite the equal sides are known to be equal. As a result, ∠A and ∠B are equal.

Isosceles Triangle Sides

An isosceles triangle has two equal sides and two equal angles. The two equal-length sides of an isosceles triangle are termed the legs, while the third side of the triangle is called the base. Although an equilateral triangle is also an isosceles triangle, the opposite is not necessarily true.

Also check: Types of Triangles in Maths based on Sides

Isosceles Triangle Angles

An isosceles triangle has three angles like a triangle, but it is a peculiar instance since two of the three angles of the isosceles triangle are equal in measure, which is opposite to the equal sides. As a result, one of the angles is uneven. The Isosceles triangle has the same angle sum property as the triangle. If we are given the measure of an uneven angle, we can simply use the angle sum property to determine the other two angles.

Assume we have an isosceles triangle ABC, with AB = AC and B = C. If we know the unknown angle A, we can easily find the other angle of the Isosceles triangle.

Example: Consider the isosceles triangle ABC, where B = C and A = 70°. Find out other angles.
Solution:
We all know that any Triangle △ABC
∠A + ∠B + ∠C = 180°
Furthermore, B = C and A = 70°
Using the triangle’s angle sum feature,
70° + ∠B + ∠B = 180°
⇒ 2∠B = 110°
⇒ ∠B = 55°
As a result, the other two angles of an isosceles triangle have a measure of 55°.

Isosceles Triangle Properties

Every geometric shape differs and is unique from the others in some ways. Thus isosceles triangle also has some unique properties that make it unique. The properties of  isosceles triangle are as follows:

• An isosceles triangle has two equal sides as well as two equal angles.
• The two equal sides legs of an isosceles triangle are known as legs., and the angle between them is known as the vertex angle or apex angle.
• The apex angle or vertex angle of an isosceles triangle is the angle formed by the legs.
• The perpendicular drawn from the apex angle cuts the isosceles triangle’s base and the apex angle in half.
• The perpendicular traced from the apex angle divides the isosceles triangle into two congruent triangles and is also known as the line of symmetry of the isosceles triangle.

Isosceles Triangle Theorem

According to the isosceles triangle theorem, if two sides of an isosceles triangle are congruent, then the angles opposing the two sides are also congruent.

The contrary of this isosceles triangle theorem is also valid, which asserts that if two angles of an isosceles triangle are congruent, then the sides opposite to them are likewise congruent.

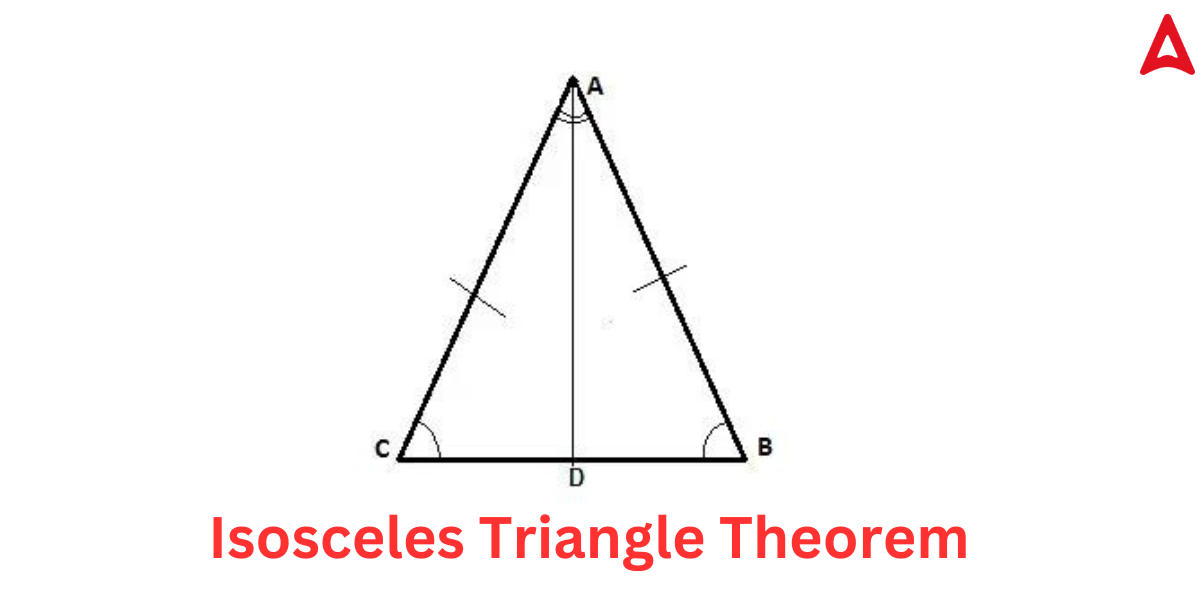
In the ABC triangle shown above,
AB = AC
∠ABC = ∠ADC

Isosceles Triangle Types

The isosceles triangle is generally divided into three different types based on the angle formed by the two legs, which are as follows:

• Isosceles acute triangle
• Isosceles right triangle
• Isosceles obtuse triangle

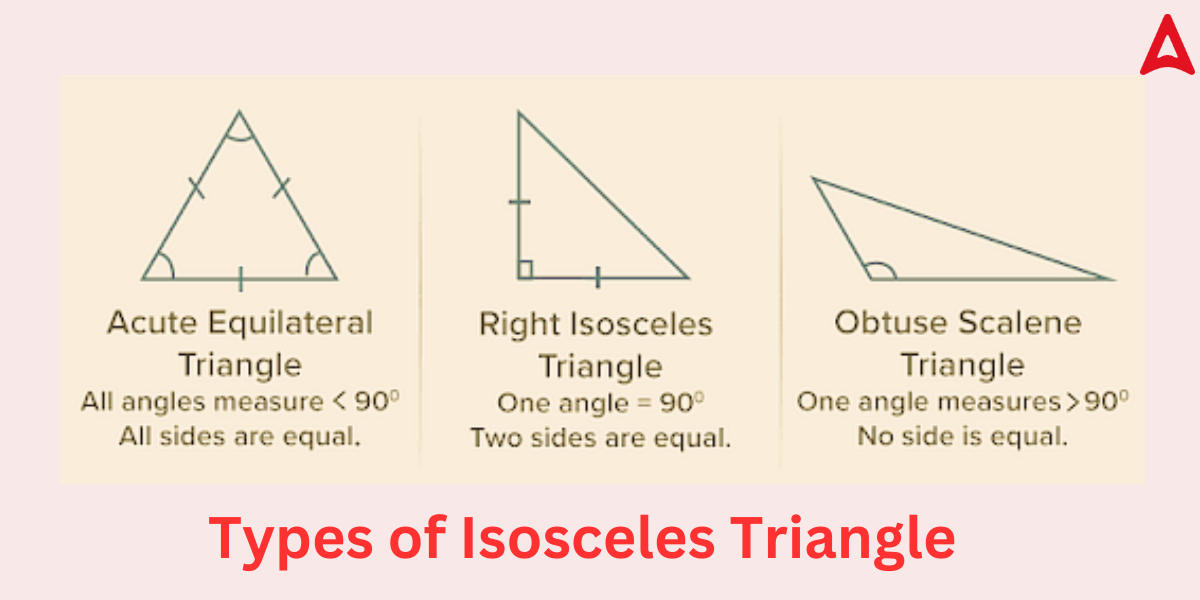
Isosceles acute triangle: If the two angles opposing the legs are equal and smaller than 90 degrees, the isosceles triangle might be acute. An Isosceles Acute triangle is an isosceles triangle with all of its angles acute.

Isosceles Right triangle: An Isosceles Right triangle is an isosceles triangle with a right angle. A right isosceles triangle has two equal sides, one of which acts as a perpendicular and the other as the triangle’s base. The hypotenuse refers to the third unequal side.

Isosceles obtuse triangle:  The obtuse triangle is defined as a triangle with one of its angles greater than 90 degrees (right angle). Isosceles obtuse triangles are isosceles triangles in which one of the angles is obtuse and the other two are acute.

Isosceles Triangle Formula

An isosceles triangle is a two-dimensional three-sided shape. As a 2-dimensional figure, it has three basic formulas of an isosceles triangle height, perimeter, and area. Let’s look at the isosceles triangle formulas for area, height, and perimeter in more detail.

Isosceles Triangle Area Formula

The area of isosceles triangle is defined as the region occupied by an isosceles triangle in two-dimensional space. In general, the base and height of an isosceles triangle are half the product of their product. The area of Isosceles triangle can be calculated using the following formula:

Area of isosceles triangle formula A = ½ × b × h Square units

where b is the triangle’s base and h is its height.

Read: Area-of Triangle Formula & Examples

Isosceles Triangle Perimeter Formula

The Perimeter of Isosceles Triangle is the shape’s boundary. The perimeter of an isosceles triangle is equal to the sum of its three side lengths. Knowing the base and side of an isosceles triangle will help us calculate its perimeter. The formula for calculating the perimeter of an isosceles triangle is as follows:

The perimeter of an isosceles Triangle, P = 2a + b unit

where ‘a’ is the length of an isosceles triangle’s two equal legs and b is the triangle’s base.

Also Check: Perimeter of the Triangle Formula & Examples

Isosceles Triangle Height Formula

When a perpendicular drawn from the apex angle splits the isosceles triangle’s base and the apex angle in half. The two congruent triangles are formed as it bisects the base. If the side lengths of an isosceles triangle are known, then the following formula can be used to determine its height:

 The Isosceles Triangle Height Formula is (h) =   

units

Sharing is caring!