Prime numbers can be further divided into various sub-categories based on their specialties. Some such types are twin prime numbers, even prime numbers, co prime numbers. In this post, we will study about the co prime numbers in detail.
Co Prime Number
Co prime numbers are ones with just one common factor in common, which is 1. To put it another way, a pair of numbers is said to be co-prime if their highest common factor is 1. Co-prime numbers can be defined in a variety of ways. You will learn about coprime numbers in mathematics along with how to spot them using a few easy tips and tricks and some practical examples here.
Coprime Numbers
Coprime numbers, also known as relatively prime or mutually prime numbers, are two integers that share no common positive integer divisors other than 1. In other words, their greatest common divisor (GCD) is equal to 1.
For example, consider the numbers 15 and 28:
- The divisors of 15 are 1, 3, 5, and 15.
- The divisors of 28 are 1, 2, 4, 7, 14, and 28.
The only positive integer that both 15 and 28 have in common as a divisor is 1. Therefore, 15 and 28 are coprime numbers because their GCD is 1.
Here are a few more examples of coprime pairs:
- 8 and 15 (GCD = 1)
- 7 and 22 (GCD = 1)
- 20 and 49 (GCD = 1)
Coprime numbers are important in number theory and various mathematical applications, including cryptography and modular arithmetic. When two numbers are coprime, it means they do not share common factors other than 1, making them suitable for certain mathematical operations and calculations.
Co Prime Number Definition
Two numbers are said to be coprime (or relatively prime) if they share no common positive integer factors other than 1. In other words, the greatest common divisor (GCD) of two coprime numbers is 1.
For example, consider the numbers 15 and 28.
The factors of 15 are 1, 3, 5, and 15. The factors of 28 are 1, 2, 4, 7, 14, and 28.
The only positive integer that is a common factor of both 15 and 28 is 1. Therefore, 15 and 28 are coprime because their GCD is 1.
Coprime numbers are important in number theory and have various applications in mathematics, including in the study of modular arithmetic and cryptography.
What are Co Prime Number?
Assume that x and y are two positive integers, and that they are coprime numbers if and only if they share only the number 1 as a common factor, with the result that HCF(x, y) = 1. The highest common factor (HCF) of co-prime numbers, or a group of numbers or integers, is 1, making 1 their only common factor. Relatively prime or mutually prime numbers are other names for co-prime numbers. In order to create co-prime numbers, two numbers are required.
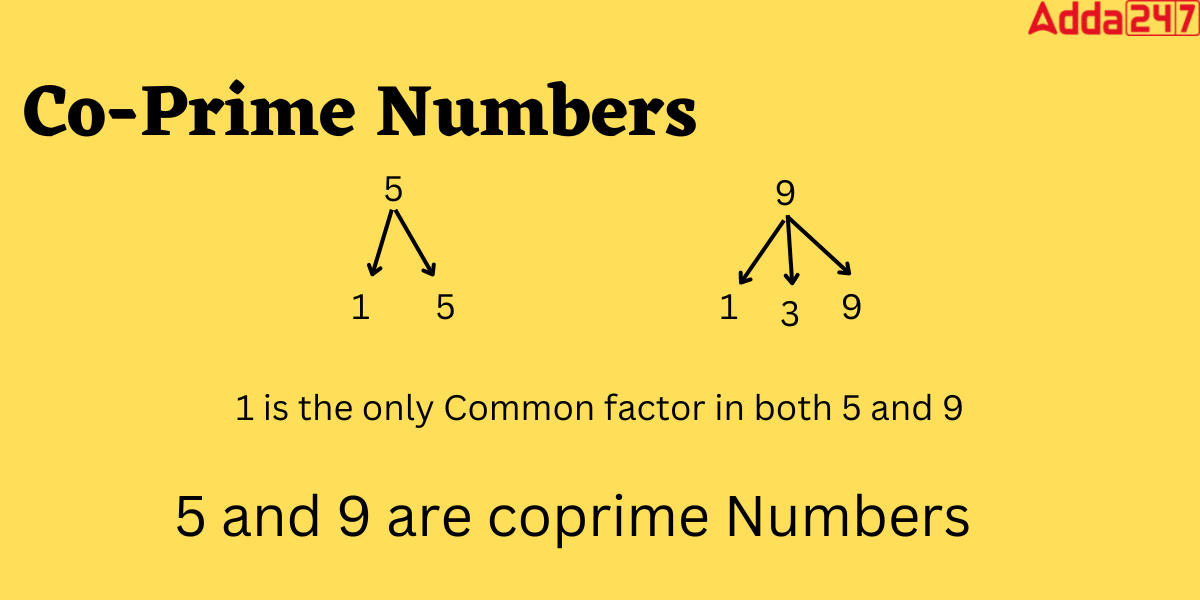
Methods to Find Co Prime Numbers
Take a set of two numbers, if they have no positive integer that can divide both, other than 1, the pair of numbers is co-prime.
Example 1: 15 and 16
Factors of 15 are 1, 3, 5, 15
Factors of 16 are 1, 2, 4, 8, 16
Here 15 and 16 have only one common factor which is 1. Hence, their HCF is 1, and are co-prime.
Example 2: 22 and 23
Factors of 22 are 1, 2, 11, 22
Factors of 23 are 1 and 23
Here 22 and 23 have only one common factor which is 1. Hence, their HCF is 1, and are co-prime.
Co Prime Number List
The below table shows the list of co prime numbers:
| Co prime Number with | Co prime numbers pairs |
| 1 | (1, 2), (1, 3), (1, 4), (1, 5) (1, 6),….., (1, 20),…. |
| 2 | (2, 3), (2, 5), (2, 7), (2, 9), …, (2, 15),….. |
| 3 | (3, 4), (3, 5), (3, 7), (3, 10), (3, 11),…., (3, 20),… |
| 4 | (4, 5), (4, 7), (4, 9), (4, 11), (4, 13), (4, 15),…. |
| 5 | (5, 6), (5, 7), (5, 8), (5, 9), (5, 11), (5, 12),… |
Properties of Coprime Numbers
The following are a few of the characteristics of co-prime numbers. These are referred to as “tricks” for fast determining pairs of coprime numbers.
- Every number and 1 are co-prime.
- Any pair of prime numbers is a coprime pair: Every prime number only has the number itself and the component 1, hence the only factor that two prime numbers will have in common is 1. For instance, two prime integers are 2 and 3. Factors of two are one, two, and three are one, three. They are co-prime because they only share the number one in common.
- Any two consecutive integers or numbers are invariably co-prime: Any string of consecutive numbers, such as 2, 3, 4, 5, 6, and so on, has 1 as its HCF.
- Any two co-prime numbers added together will always have a co-prime product. Coprime numbers 2 and 3 have a sum of 5 and a product of 6 (2+3). 5 and 6 are hence co-prime to one another.
- Since all even numbers have the same factor 2, two even numbers can never be combined to make a coprime pair.
- Two numbers are not coprime to one another if they have the unit digits 0 and 5 respectively. For instance, because their HCF is 5 (or divisible), 10 and 15 are not coprime.
Co Prime Numbers One to Hundred (1-100)
Co prime numbers between 1 to 100 are given below which follows all the above properties
(13, 14)
(28, 57)
(1, 99)
(2, 97)
(46, 67)
(75, 41) and so on.
Additionally, we can express every integer as a pair of coprime numbers, such as (22, 1), (31, 1), (4, 1), and (90, 1) (1, 100). Numerous coprime numbers between 1 and 100 are defined in this way.
Co Prime Numbers and Twin Prime Numbers
The HCF of an integer that is co-prime is 1. Twin prime numbers, on the other hand, are prime numbers whose difference is always 2. For instance, the prime numbers 3 and 5 are twins. The distinctions between co-prime and twin prime numbers are listed in the paragraphs that follow.
- Co-prime numbers can also be composite numbers, however twin prime numbers are always prime.
- Unlike the difference between two co-primes, which can be any number, the difference between two twin primes is always 2.
- While all co-prime numbers may or may not be twin primes, all pairs of twin prime numbers are also co-prime.
- Every number and 1 form co-prime pairs, but only 3 and 1 create twin prime pairs.
What are Coprime Numbers
A prime number is a number that only has itself and the number one as a factor.
However, Coprime Numbers are only taken into account in pairs, and two Numbers are CoPrime if and only if they share a common factor of 1. HCF for them is 1.
Co Prime Number Example
Que. Check whether the numbers are co-prime or not from the given set of numbers
- 14 and 16
- 33 and 34
- 5 and 6
Solutions:
- 14 and 16 are not co-prime because their common factors are 1 and 2
- 33 and 34 are co-prime because their common factor is 1 only.
- 5 and 6 are co-prime because their common factor is 1 only.
| Related Articles | |
| Even Numbers | Odd Numbers |
| Co-Prime Number | Integers |
| Ordinal Numbers | Roman Numbers |











 Jawahar Navodaya Vidyalaya Admission For...
Jawahar Navodaya Vidyalaya Admission For...
 Karnataka DCET Seat Allotment Result 202...
Karnataka DCET Seat Allotment Result 202...
 AP POLYCET Seat Allotment Result 2025 OU...
AP POLYCET Seat Allotment Result 2025 OU...









