Cube Formula, Surface area and Volume Formulas in Maths

Cube

A cube is a three-dimensional solid object with six square faces, facets, or sides, three of which meet at each vertex in geometry. The cube is one of the five Platonic solids and is the only regular hexahedron. It consists of six faces, twelve edges, and eight vertices. A square parallelepiped, an equilateral cuboid, and a right rhombohedron are all examples of the cube. In three orientations, it’s a standard square prism, and in four, it’s a trigonal trapezohedron. The octahedron and the cube are twins. Its symmetry is cubical or octahedral. The only convex polyhedron with entirely square faces is the cube.

Figure: A 3D CUBE

Cube Formula

the cube formula refers to the mathematical formula used to calculate the volume and surface area of a cube.

Volume of a Cube: The volume of a cube can be found by raising the length of one side (also known as the edge) of the cube to the power of 3. Mathematically, the formula for the volume (V) of a cube is:

V = s^3

Here, “s” represents the length of one side of the cube. So, to find the volume, you simply need to multiply the side length by itself twice.

Surface Area of a Cube: The surface area of a cube is the total sum of the areas of all its six sides. Since all sides of a cube are equal in length, the formula for the surface area (A) of a cube is:

A = 6s^2

In this formula, “s” represents the length of one side of the cube. To calculate the surface area, you need to multiply the side length by itself, then multiply by 6 to account for all six sides.

Remember, these formulas apply specifically to cubes, which are three-dimensional objects with equal side lengths.

Area of Cube Formula

What is Area of a Cube?

The total area covered by all six faces of the cube is known as the cube’s surface area. Calculating the area of the two bases and the area of the four lateral sides yields the total surface area of a cube. The area of the cube will be equal to the sum of the area of the cube’s bases and lateral surfaces. The overall surface area of the cube will be the surface area of one face multiplied by six because all six faces are made up of squares of the same dimensions.

There are two types of Area of a cube:

Total Surface area of a cube
Lateral Surface area of a cube

Total Surface Area of a Cube

A cube’s total surface area refers to the total area covered by all six of its faces. The sum of the areas of these 6 faces is used to compute the Total Surface Area of a cube.

Lateral Surface Area of a Cube

The total area covered by a cube’s side or lateral faces is referred to as the lateral surface area. To compute Lateral Surface Area, we add the areas of these four faces together.

How to Find the Surface Area of a Cube?

Total Surface Area of a Cube

The total surface Area of the cube is calculated by doing the product of the square of its side length by 6. Therefore, the formula for the surface area of the cube, which has a side length a units is:

Total Surface Area of a Cube = 6a² square units

Lateral Surface Area of a Cube

The lateral surface Area of the cube is calculated by doing the product of the square of its side length by 4. Therefore, the formula for the lateral surface area of the cube, which has a side length a units is:

Lateral Surface Area of a Cube = 4a² square units

Cube Formula: Volume of a Cube

What is Volume of a Cube?

The entire number of cubic units totally occupied by a cube is defined as its volume. A cube is a solid three-dimensional shape with six square faces. The total space occupied by an object is defined as its volume. Because the cube’s faces are all square in shape, the length of its edges will be equal. As a result, the cube’s length, breadth, and height are all equal. The number of cubic units totally occupied by a cube is defined by its volume. The volume of a cube is measured in cubic units such as cm^3, m^3,, along with other units.

How to find Volume of a Cube?

The volume of a cube can be calculated by doing the of the edge length three times. Therefore, the formula to calculate the volume of a cube with side length of the cube as s units is:

Volume of a cube = a³ cubic units

The diagonal of a cube is equals to √3a, where, a is the side length of the cube. By the use of this formula, it can be inferred that

a = d/√3 units

where d is the length of the diagonal of the cube.

Therefore, the volume of cube using the diagonal can is:

Volume of Cube = √3 × d³/9 cubic units

Cube formula in mensuration class 10

Mostly we all use to play with dice and Rubik’s cubes in childhood. And these are examples of a cube. A cube is a solid shape in a three-dimensional plane, having 6 faces of equal length. There is some cube formulas for determining the Total surface area, Volume. In this topic, we learn about cube formulas along with some solved examples.

Cube formula: What is a cube?

In geometry, the cube is a three-dimensional solid shape consisting of square-shaped six faces of equal size. All the angles of the cube are a right angle or 90°. Some examples of a cube are -dice, Rubic’s cube, square ice cubes, sugar cubes, etc. Let’s summarize the properties of a cube.

Cube formula: Properties of a cube

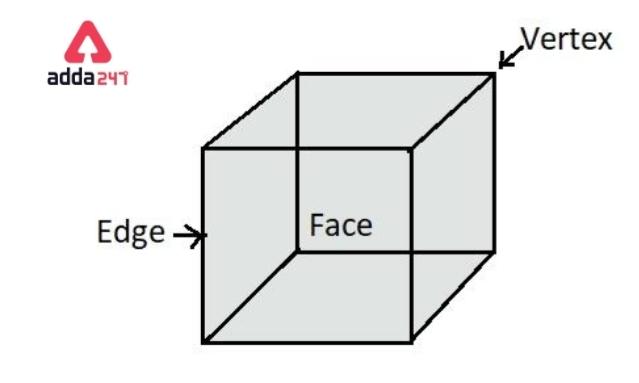
A cube is a three-dimensional solid object having six equal square-shaped faces.

Properties of a cube are –
• All 6 faces of the cube are square-shaped and equal in size.
• Cube has a total of 12 edges with equal length. All 12 edges are parallel to their opposite edge.
• There is a total of 12 diagonals on the surface area of the cube. ( 2 diagonals on each face). All of the 12 are equal.
•A cube has a total of 8 vertices.
• All the angles of the cube are a right angle or 90°.

• All the 4 space diagonals are also equal in length.

Cube formula surface area

The surface area of a cube is the sum of areas of a total of six faces. We can classify the surface area as-
• Lateral Surface area (LSA) – Lateral surface area or LSA defines the sum of areas of all 4 faces excluding the areas of the top and bottom faces of that cube. The formula by which we can find out the LSA of a cube is – 4 × ( edge )²
Let’s assume, Edge of a cube is – ‘a’.
Lateral surface area – 4 × a² square units.
• Total surface area (TSA) – Total surface area or TSA is the sum of areas of a total of six faces. The formula for determining the total surface area of a cube is,
Total surface area(TSA) = 6 ×(edge)²
Let’s consider, Edge of a cube is – ‘a’.
Total surface area(TSA) = 6 × a² Square units

Cube formula volume

The volume of a cube is described as the holding capacity of the cube. If the length of one edge is given, we can easily find out the volume of a cube.
The cube formula for volume is – (edge)³ or a³ cube units, where ‘a’ is the length of the edge.

Cube formula diagonal

In geometry, a diagonal is a slant line segment that runs between two opposite corners of a shape. In a cube, There is a total of 12 equal diagonals on the surface of the cube ( 2 diagonals on each face), and 4 space or internal diagonals are also equal in length. We can calculate the length of diagonals on the face of the cube by multiplying the edge length by √2 and calculate the length of internal diagonals by multiplying the edge length by √3.
If the length of one edge of a cube is a unit, then
The length of a Diagonal on the surface area is-√2 × a units
The length of an internal Diagonal is – √3 × a units

Cube formula Perimeter

The perimeter of a cube defines the sum of all edges of that cube. The formula to obtain the perimeter of a cube is – 12 × edge or 12 ×a units, where ‘a’ is the length of the edge.

Cube formula list

Here is a list of some important cube formulas. Let’s assume the length of the edges of a cube is equal to a unit.

Cube formula for volume	(edge)³ or a³ cube units
Lateral surface area (LSA)	4 × ( edge )² or 4 × a² square units.
Total surface area(TSA)	6 × ( edge )² or 6 × a² Square units
Length of an internal Diagonal	√3 × edge or √3 × a units
The perimeter of a cube	12 × edge or 12 ×a units

Cube formula mensuration examples with answer

Q. Length of the edges of a cube is equal to 6 cm. Calculate the volume of the cube?
Solution- we knew that the formula for the volume of a cube is – (edge)³ or a³ cube units, where ‘a’ is the length of the edges of the cube.
In the given cube length of one edge is 6 cm. (a=6 cm)
So, the volume of the cube is = 6³ cubic cm
V= 216 cm³ (Answer)
Q.What is the length of the edges of the cube whose total surface area is 294 cm².
Solution- Let’s assume the length of edges -a cm
The formula to determine the total surface area of a cube is – 6 a² square. where ‘a’ is the length of the edges of the cube.
Here given the cube’s total surface area is- 294 cm²
6a² = 294
or, a² = 294/6 = 49
or, a = 7 cm [ we always consider a positive value because length can’t be negative]

Q. Find out the total surface area of a cube with an edge length of 4 cm?
Solution- To the given information, the length of the edge of the cube is 4 cm.
The formula for the total surface area of a cube is -6 a² squares units. where ‘a’ is the length of the edges of the cube,
TSA = 6 × 4 ² cm²
TSA = 96 cm²
Answer – The total surface area of the cube is – 96cm²

Q. What is the length of an internal diagonal of the cube having a side length of 8 cm.
Solution- The length of an internal Diagonal is – √3 × a unit.where ‘a’ is the length of the edges of the cube.
In the given cube, the length is 8 cm.
So, the Length of an internal Diagonal of that cube is
= 8 √3 units. (Answer)

Cube formula exercise

The perimeter of the cube is 108 cm. what is the side length of the cube?
Find out the volume of a cube with an edge length of 12 cm.
What is the length of the edges of the cube whose volume is 2744 cm²?
Calculate the perimeter of the cube having a side length of 9 cm.

Cube Formulas in Hindi

घन सूत्र: घन का क्षेत्रफल

घन का क्षेत्रफल क्या होता है?

घन के सभी छह फलकों द्वारा कवर किए गए कुल क्षेत्रफल को घन के सतह क्षेत्र के रूप में जाना जाता है। दो आधारों के क्षेत्रफल और चार पार्श्व भुजाओं के क्षेत्रफल की गणना करने से घन का कुल पृष्ठीय क्षेत्रफल प्राप्त होता है। घन का क्षेत्रफल घन के आधारों और पार्श्व सतहों के क्षेत्रफल के योग के बराबर होगा। घन का समग्र पृष्ठीय क्षेत्रफल एक फलक का पृष्ठीय क्षेत्रफल छह से गुणा होगा क्योंकि सभी छह फलक समान आयामों के वर्गों से बने होते हैं।

घन के क्षेत्रफल दो प्रकार के होते हैं:

घन का कुल पृष्ठीय क्षेत्रफल
घन का पार्श्व पृष्ठीय क्षेत्रफल
एक घन का कुल पृष्ठीय क्षेत्रफल

एक घन का कुल पृष्ठीय क्षेत्रफल उसके सभी छह फलकों द्वारा कवर किए गए कुल क्षेत्रफल को दर्शाता है। इन 6 फलकों के क्षेत्रफलों के योग का उपयोग घन के कुल पृष्ठीय क्षेत्रफल की गणना के लिए किया जाता है।

घन का पार्श्व पृष्ठीय क्षेत्रफल

घन की भुजा या पार्श्व फलकों द्वारा कवर किए गए कुल क्षेत्रफल को पार्श्व पृष्ठीय क्षेत्रफल कहा जाता है। पार्श्व सतह क्षेत्र की गणना करने के लिए, हम इन चार चेहरों के क्षेत्रों को एक साथ जोड़ते हैं।

घन का क्षेत्रफल कैसे ज्ञात करें?
एक घन का कुल पृष्ठीय क्षेत्रफल

घन के कुल पृष्ठीय क्षेत्रफल की गणना उसकी भुजा की लंबाई के वर्ग के गुणनफल को 6 से करने पर की जाती है। इसलिए, घन के पृष्ठीय क्षेत्रफल का सूत्र, जिसकी एक भुजा की लंबाई एक इकाई है, है:

घन का कुल पृष्ठीय क्षेत्रफल = 6a2 वर्ग इकाई
घन का पार्श्व पृष्ठीय क्षेत्रफल

घन के पार्श्व सतह क्षेत्र की गणना इसकी भुजा की लंबाई के वर्ग के गुणनफल को 4 से करके की जाती है। इसलिए, घन के पार्श्व सतह क्षेत्र के लिए सूत्र, जिसकी एक भुजा की लंबाई एक इकाई है:

घन का पार्श्व पृष्ठीय क्षेत्रफल = 4a2 वर्ग इकाई

घन सूत्र: घन का आयतन

घन का आयतन क्या है?

एक घन द्वारा पूरी तरह से व्याप्त घन इकाइयों की पूरी संख्या को इसके आयतन के रूप में परिभाषित किया जाता है। एक घन छह वर्गाकार फलकों वाला एक ठोस त्रि-आयामी आकार है। किसी वस्तु द्वारा कब्जा किए गए कुल स्थान को उसके आयतन के रूप में परिभाषित किया जाता है। चूँकि घन के सभी फलक वर्गाकार हैं, इसलिए इसके किनारों की लंबाई बराबर होगी। नतीजतन, घन की लंबाई, चौड़ाई और ऊंचाई सभी बराबर हैं। एक घन द्वारा पूरी तरह से व्याप्त घन इकाइयों की संख्या को इसके आयतन से परिभाषित किया जाता है। घन का आयतन अन्य इकाइयों के साथ घन इकाइयों जैसे cm3, m3, में मापा जाता है।

घन का आयतन कैसे ज्ञात करें?

एक घन के आयतन की गणना किनारे की लंबाई को तीन बार करके की जा सकती है। इसलिए, घन की भुजाओं की लंबाई वाले घन के आयतन को s इकाइयों के रूप में परिकलित करने का सूत्र है:

घन का आयतन = a3 घन इकाई

एक घन का विकर्ण √3a के बराबर होता है, जहाँ, एक घन की भुजा की लंबाई है। इस सूत्र के प्रयोग से यह अनुमान लगाया जा सकता है कि

ए = डी/√3 इकाइयां

जहाँ d घन के विकर्ण की लंबाई है।

इसलिए, विकर्ण कैन का उपयोग करने वाले घन का आयतन है:

घन का आयतन = 3 × d3/9 घन इकाई

Related Post:

Cube formula: QNAs

Q. How many edges are present in a cube?

A- There are a total of 12 edges present in a cube.

Q. What is the formula for calculating the total surface area of a cube?

A-Total surface area or TSA is the sum of areas of a total of six faces. The formula for determining the total surface area of a cube is,
Total surface area(TSA) = 6 ×(edge)²

Q. What is the difference between a cube and a cuboid?

A- The main difference between a cube and a cuboid is, that the cube has six square-shaped equal faces and on another hand, the cuboid has six rectangular equal shaped faces.

Q. How to calculate the volume of a cube?

A-We can calculate the volume of a cube by using the following formula,

The cube formula for volume is – (edge)³ or a³ cube units, where ‘a’ is the length of the edge.

Q. Write down the formulas for determining the surface area of a Rubik’s cube?

A- The Surface area of a Rubik’s cube is the sum of areas of a total of six faces. We can classify the surface area as (A) Lateral surface area – 4 × a² square units. (B)Total surface area(TSA) = 6 × a² Square units, where ‘a’ is the length of the edges of the cube.

Q. What is Cube Formula?

A- Following are the Cube Formulae:

Total Surface Area of a Cube = 6a² square units
Lateral Surface Area of a Cube = 4a² square units
The volume of a cube = a³ cubic units
The volume of Cube = √3 × d³/9 cubic units

where a is the length of the side of a cube and d is the length of the diagonal of a cube.

Q. What is the Formula for area for cubes?

A- There are two types of areas of a cube:

Total Surface Area of a Cube = 6a² square units
Lateral Surface Area of a Cube = 4a² square units

Q. How many Formulas are there in the cube?

A- There are four Formulae for the cube:

For the calculation of the Total Surface Area
For the calculation of Lateral Surface Area
For the calculation of the Volume of a cube using the sides of a cube
For the calculation of the Volume of a cube using the diagonals of a cube

What is the cuboid area?

In order to find the area of a cuboid, we need to calculate the area of all the six faces of that cuboid and then add the area of all the six faces. There are two faces with the area as length × breadth, two faces with the area as breadth × height, and two faces with the area as height × length. Therefore the total surface area of a cuboid is:

Total Surface area = 2 {(length × breath) + (breadth × height) + (height × length)}