Median Formula for Even, Odd Number for Class 10 -

Median

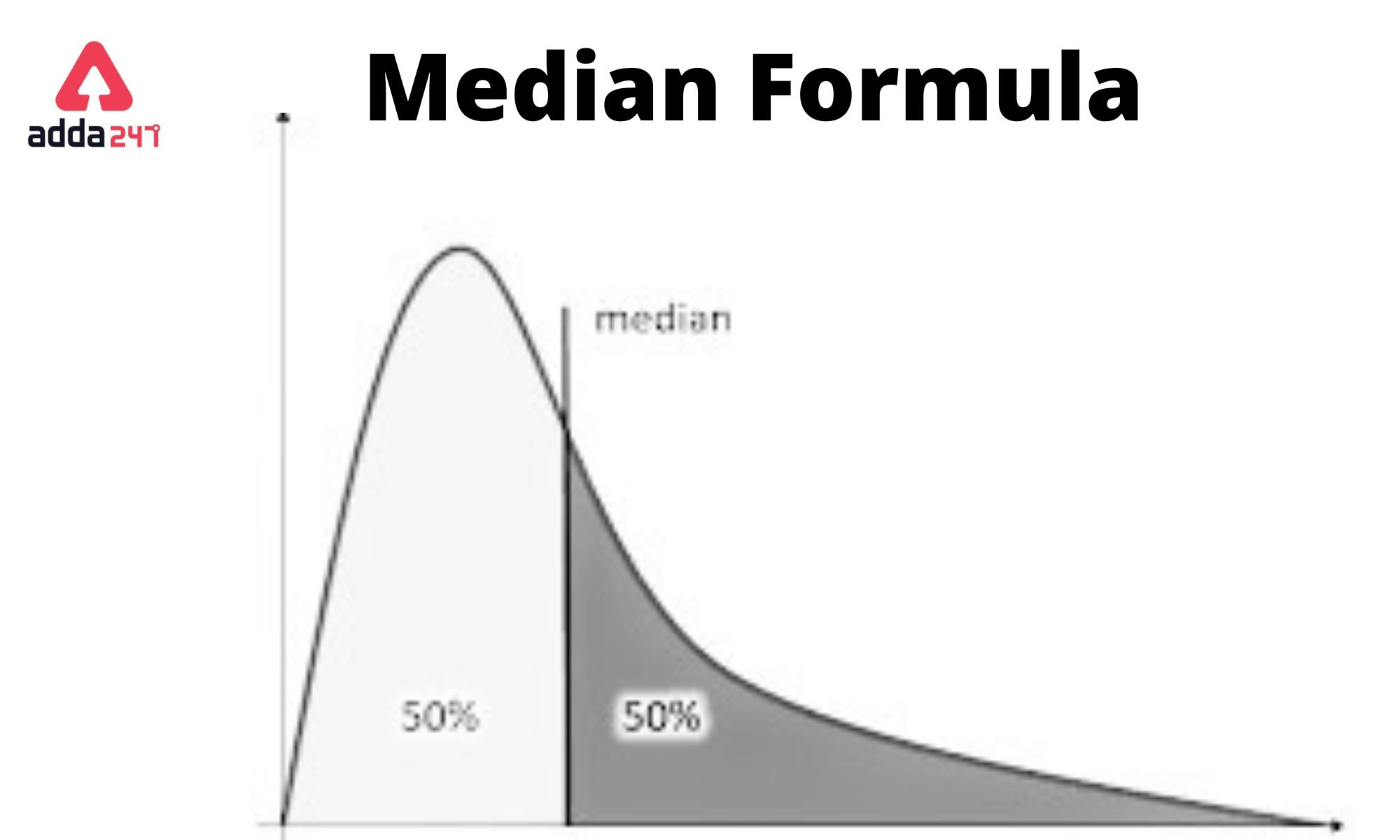
For each group, the median is the value in the middle. It’s where half of the data is more and half of the data is less. The median makes it possible to represent a vast number of data points with just one. The median is the most straightforward statistical measure to compute. The data must be sorted in ascending order to calculate the median, and the middlemost data point is the data’s median.

Median Definition

The median of the data is the value of the middle-most observation obtained after arranging the data in ascending order. In many cases, it is difficult to evaluate all of the data for representation, hence the median comes in handy. The median is a simple metric to calculate among the statistical summary metrics. Because the data in the middle of a sequence is regarded as the median, the median is also known as the Place Average.

Median Formula

The median is a statistical measure that represents the middle value in a set of data. It is the value that separates the data into two equal halves, with half of the values being greater than the median and half being smaller.

The formula for finding the median depends on whether the dataset has an odd or even number of values:

Odd Number of Values:
- Arrange the data in ascending order.
- The median is the value in the middle of the ordered data set.
Example: For the data set {3, 1, 4, 2, 5}, the median is 3. The values are arranged in ascending order as {1, 2, 3, 4, 5}, and the middle value is 3.
Even Number of Values:
- Arrange the data in ascending order.
- The median is the average of the two middle values.
Example: For the data set {7, 2, 4, 9, 1, 5}, the median is (4 + 5) / 2 = 4.5. The values are arranged in ascending order as {1, 2, 4, 5, 7, 9}, and the two middle values are 4 and 5. Their average is 4.5.

In both cases, it is important to arrange the data in ascending order before determining the median. This ensures that the middle value(s) accurately represents the central tendency of the dataset.

Median Formula for Even and Odd Number

Median of a given data is given by the formula:

$\mathrm{Med}(X) = \begin{cases} X[\frac{n}{2}] & \text{if n is even} \\ \frac{(X[\frac{n-1}{2}] + X[\frac{n+1}{2}])}{2} & \text{if n is odd} \end{cases}$

where X is the list on order of values of a given set of data,

and n refers to the number of values in the given set of data.

Mean Mode Median Formula

formulas for mean, mode, and median:

Mean: The mean, also known as the average, is calculated by summing up all the values in a dataset and then dividing by the number of values.Mean = (Sum of all values) / (Number of values)
Mathematically: Mean = (x1 + x2 + x3 + … + xn) / n

The mean, also known as the average, is a measure of central tendency that provides the typical value of a set of data. The formula for calculating the mean of a dataset is as follows:

Mean = Sum of all values / Number of values

In other words, to find the mean:
1. Add up all the values in the dataset.
2. Divide the sum by the total number of values in the dataset.
For example, let’s calculate the mean of the following dataset: {10, 15, 20, 25, 30}.

Sum of all values = 10 + 15 + 20 + 25 + 30 = 100 Number of values = 5

Mean = Sum of all values / Number of values = 100 / 5 = 20

So, the mean of the dataset {10, 15, 20, 25, 30} is 20.

The mean provides a measure of the central value or average of a dataset, making it useful for understanding the overall tendency of the data.
Mode: The mode is the value that appears most frequently in a dataset. A dataset can have no mode (when all values are unique) or multiple modes (when multiple values have the same highest frequency).The mode is a measure of central tendency that represents the value(s) that appear most frequently in a dataset. In class 10, the mode is typically calculated by determining the value(s) that occur with the highest frequency. There is no specific formula for finding the mode; it involves identifying the value(s) that occur most often in the dataset.
Here’s an example to illustrate how to find the mode:

Consider the following dataset: {2, 4, 6, 4, 8, 4, 10, 4, 6}

In this dataset, the number 4 appears most frequently, occurring four times. Therefore, the mode of this dataset is 4.

In some cases, a dataset may have multiple modes, meaning that two or more values occur with equal frequency and are the most common. For example, in the dataset {2, 4, 6, 4, 8, 4, 10, 6}, both 4 and 6 appear twice, making them both modes of the dataset.

It’s important to note that a dataset may also have no mode if no value is repeated or if all values occur with the same frequency.

Calculating the mode helps identify the most common values in a dataset, providing insights into its distribution and frequently occurring elements.
Median: The median is the middle value in a dataset when the values are arranged in order. If there’s an odd number of values, the median is the middle one. If there’s an even number of values, the median is the average of the two middle values.For an odd number of values: Median = Middle Value
For an even number of values: Median = (Value at Position n/2) + (Value at Position n/2 + 1) / 2

Where n is the total number of values in the dataset.

Remember that the mean, mode, and median are measures of central tendency used to describe different aspects of a dataset’s distribution. The mean is sensitive to outliers, the mode indicates the most frequent value, and the median is less affected by extreme values.

Median Formula For Grouped Data

Data that has been categorised is referred to as grouped data. This type of data can be displayed using histograms and frequency tables.

Formula for finding median of a grouped data set is:

Median = l +[ {(n/2) – cf} / f ] × h

Median Formula For Ungrouped Data

The first data you collect from an experiment or study is ungrouped data. The data is unprocessed, meaning it hasn’t been categorised, classified, or otherwise grouped. A list of numbers is what an ungrouped piece of data is.

Formula for finding median of an ungrouped data set is:

Median Formula For odd Number of Observations

Median = [(n+1)/2]^th observation,

where n is odd.

Median Formula For Even Number of Observations

Median = mean of (n/2)^thobservation and [(n/2)+1]^thobservation,

where n is even.

Relationship between Median, Mean, and Mode

Karl Pearson explains the relationship between mean median and mode with the help of his Formula as:

Mean – Median = $\frac{1}{(3)}$ (Mean – Mode)

=> 3(Mean – Median) = Mean – Mode

=> Mode = Mean – 3 (Mean – Median)

=> Mode = 3 Median – 2 Mean

Therefore, by using the obtained equation, we can find the value of one of the three if the value of the other two is given.

What is how do you find the median of ungrouped data when each number of observations were given?

To find the median of ungrouped data when each individual observation is given, you can follow these steps:

Organize the Data: Arrange the individual observations in ascending order from smallest to largest.
Count the Observations: Count the total number of observations (n).
Identify the Middle Value(s):
- If the total number of observations (n) is odd, the median is the middle value. The position of the middle value is given by (n + 1) / 2.
- If the total number of observations (n) is even, the median is the average of the two middle values. The positions of the middle values are n / 2 and (n / 2) + 1.
Calculate the Median:
- If n is odd, the median = Value at position (n + 1) / 2.
- If n is even, the median = (Value at position n / 2) + (Value at position (n / 2) + 1) / 2.

Here’s an example to illustrate the process:

Suppose you have the following ungrouped data: 12, 8, 15, 6, 21, 10, 14

Organize the data in ascending order: 6, 8, 10, 12, 14, 15, 21
Count the total number of observations (n): n = 7
Since n is odd (7 is odd), the median is the middle value at position (n + 1) / 2: Median = Value at position (7 + 1) / 2 = Value at position 4 = 12

So, the median of the given ungrouped data is 12.

If you had an even number of observations, you would average the two middle values according to the steps mentioned earlier.

Related Posts:

Median Formula QNAs

How do we calculate the median?

To calculate the median, sort your data first. Then, using n, the number of values in your data collection, determine the middle position. When n is an odd integer, the median is found at (n + 1) / 2. The median is the mean of the values at positions n / 2 and (n / 2) + 1 if n is an even integer.

Whats is median?

The median of the data is the value of the middle-most observation obtained after arranging the data in ascending order. The median is the value in the middle of a list that is ranked from smallest to largest. The mode is the value in the list that appears the most frequently.

What is the mean vs median?

A data set’s mean (average) is calculated by summing all of the numbers in the set and dividing by the number of values in the set. When a data collection is ordered from least to largest, the median is the midway value. In a data set, the mode is the number that appears the most frequently.

What is median in math geometry?

A median is the line segment that connects a vertex to the opposing side’s midway. When the vertex is an angle in an equilateral triangle or the non-congruent angle of an isoceles triangle, it is also an angle bisector.

Is an altitude a median?

A triangle’s median is a line that runs from one vertex to the opposing side’s midway. A triangle’s height is a perpendicular segment connecting a vertex to the line containing its opposite side.