Value of e
The value of “e” refers to Euler’s number, a mathematical constant that is approximately equal to 2.71828. value of e is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation goes on infinitely without repeating. Euler’s number, denoted as “e,” is widely used in various branches of mathematics, such as calculus, exponential functions, and complex analysis. The value of e is a fundamental constant that appears in many mathematical and scientific formulas and equations.
Value of e in Maths
value of e: The number e, commonly known as Euler’s number, is a mathematical constant with a value of around 2.71828 that can be described in a variety of ways. value of e is the natural logarithms’ base. As n approaches infinity, it is the limit of (1 + 1/n)n, an expression that emerges in the study of compound interest. value of e is also possible to calculate it as the sum of infinite series.
In mathematics, the number e, along with the numbers 0, 1, π and i is extremely important. All five are mentioned in one version of Euler’s identity, and they all have essential and recurrent roles in mathematics. e is irrational (that is, value of e cannot be expressed as a ratio of integers) and transcendental, just like the constant (that is, it is not a root of any non-zero polynomial with rational coefficients).
Value of e in Physics
value of e: Euler’s number has a huge number of digits in its magnitude. It can go up to 1000 digits. However, we only utilise the approximated value of Euler’s number e, which is 2.72, in mathematical computations.
But, The value of e to 20 decimal places is: 2.71828182845904523536
What is the Value of e, Applications?
There are a lot of Applications of the value of e. A few of the applications of the value of e are:
- The Value of e can be used to find the Compound interest. With continued compounding, an investment with a starting balance of $1 and an annual interest rate of R would generate eRt dollars following t years.
- The Value of e can be used to determine Bernoulli’s Trials. In a method that isn’t related specifically to exponential increase, the number e has uses in probability theory.
- The Standard normal distribution can be also used as the Value of e. The standard normal distribution is a normal distribution with a mean of zero and a standard deviation of one.
- Another application of e is in the topic of derangements, generally known as the hat check problem, which was found in part by Jacob Bernoulli and in part by Pierre Remond de Montmort.
- The Value of e is aslo necessary to find the number of Asymptotes. Many problems requiring asymptotics inherently contain the number e.
E value
The seventeenth century was a period of rapid transformation. value of e was the time of the scientific revolution, colonialism’s spread, the rise of mass literacy, and a boom in international trade. The European age of exploration (and exploitation) brought various cultures from around the world into contact, conflict, and commerce on a scale that none of the previous great empires could match. The demand for capital increased as the volume of business grew. Money loans began to play an increasingly important part in the success of individuals, businesses, and countries.
Given the expanding importance of finance in the seventeenth century, historians assume the first individual to compute e would have been most likely a banker or dealer interested in compound interest’s qualities.
Read More Post:
- 17 National Symbol Of India With Names List
- Father Of Mathematics In India And The World
- IPPB Full-Form – India Post Payments Bank
- Thank You Coronavirus Helpers: Essay, Images, Messages, Pictures
- Name The Largest Delta In The World
- Projectile Motion- Definition, Formula, Derivation, Examples
- Solar Eclipse 2022 In India – Types, Occurrence, History
- Acetone Formula, Structure, Name, Uses, Reactions In Chemistry
Value of e: FAQs
Ques. What is Value of Euler of a number?
Ans. Euler’s number is a significant constant that appears in a variety of contexts and serves as the foundation for natural logarithms. Euler’s number is 2.72, an irrational number symbolized by the letter e, in which the digits carry on indefinitely in a sequence that never stops or repeats.
Ques. What is Euler’s number in fluid mechanics?
Ans. The Euler number is a dimensionless value used to analyze fluid flow dynamics situations involving a significant pressure differential between two sites. The Euler Number can be thought of as a measure of the pressure forces to inertial forces ratio.
Ques. What is Euler’s number used for in physics?
Ans. The Euler number is used to characterize energy losses inflows, and it expresses the link between a local pressure drop produced by a limitation and the kinetic energy per volume of the flow. A completely frictionless flow equates to an Euler number of zero.
Ques. Where does Euler’s number come from?
Ans. Leonhard Euler, the famous mathematician, was the one who found e and determined its value to 23 decimal places. It’s also known as Euler’s number, and it’s a transcendental number like pi (it implies that the Euler number is not the root of any algebraic equation which has integer coefficients).
Ques. When did Euler first use e?
Ans. The notation e initially apApeared in a letter Euler wrote to Goldbach in 1731, for whatever reason. In the years that followed, he made several discoveries about e, but it wasn’t until 1748 that he authored Introduction in Analysin infinitorum that he presented a comprehensive study of the theories around e.

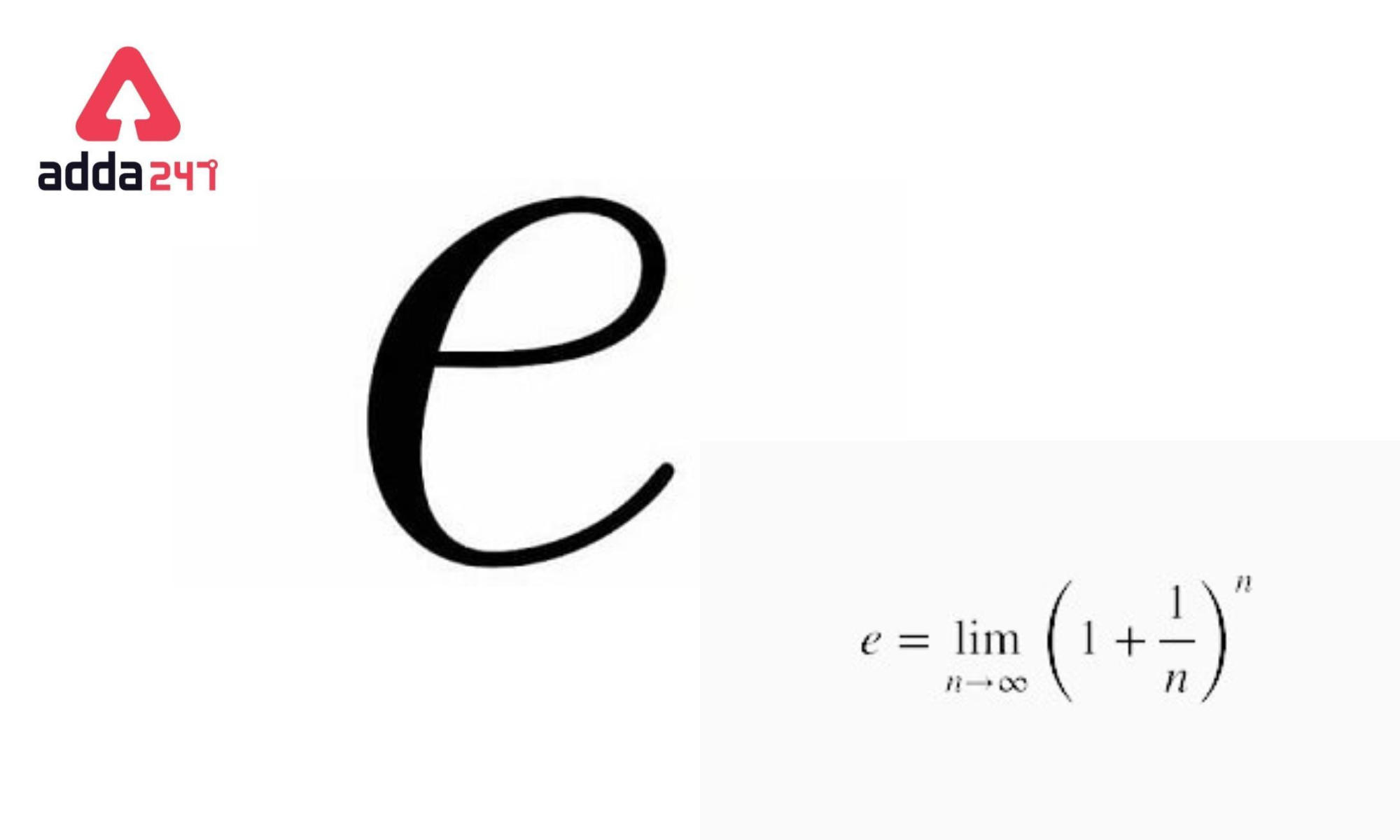








 Jawahar Navodaya Vidyalaya Admission For...
Jawahar Navodaya Vidyalaya Admission For...
 Karnataka DCET Seat Allotment Result 202...
Karnataka DCET Seat Allotment Result 202...
 AP POLYCET Seat Allotment Result 2025 OU...
AP POLYCET Seat Allotment Result 2025 OU...









