What is projectile motion with example?

All of these are examples of projectile motion: throwing a ball straight up, kicking a ball at an angle to the horizontal, or just dropping things and letting them fall freely. The only force acting on the object in projectile motion is gravity.

What is projectile called?

The motion of an item hurled or projected into the air, subject only to gravity's acceleration, is known as projectile motion. The object is known as a projectile, and the course it takes is known as a trajectory.

What causes projectile motion?

A projectile is an item on which gravity is the only force acting. Gravity influences the projectile's vertical motion, resulting in vertical acceleration. The projectile's horizontal motion is caused by the tendency for any moving item to maintain a constant velocity.

Why do we ignore air resistance?

Because air resistance is independent of mass, it is small for heavy things. This is because a force is simply an interaction that attempts to modify an object's momentum, which is determined by its mass; the higher the mass, the greater the momentum, and the more force required to change it.

Projectile Motion Formula, Equations, Examples, Derivation

Q: What are the 3 types of projectile motion?

The three types of Projectile Motion are: 1. Oblique projectile motion. 2. Horizontal projectile motion. 3. Projectile motion on an inclined plane.

Table of Contents

Projectile Motion- Definition

Projectile motion is a type of motion that an item or particle (a projectile) experiences when it is projected near the Earth’s surface and moves along a curved route only under the influence of gravity (in particular, the effects of air resistance are passive and assumed to be negligible). Galileo demonstrated that this curving path is a parabola, although it can also be a straight line when thrown directly above. Ballistics is the study of such motions, and such a trajectory termed a ballistic trajectory. The only mathematically significant force acting on the object is gravity, which operates downward, imparting a downward acceleration on the object towards the Earth’s centre of mass. The horizontal velocity component of the object’s motion does not require any external force due to its inertia. Other factors, such as aerodynamic drag or internal propulsion (as in a rocket), necessitate further investigation. A ballistic missile is a missile that is only guided during its initial powered phase of flight and then follows the principles of classical mechanics for the rest of its flight.

Read More About:

Types of Projectile Motion

There are 2 Types of Projectile Motion Identified. Which are given below.

1. Oblique Projectile Motion

2. Horizontal Projectile Motion

Projectile Motion Equations

Projectile Motion Equations are given below. Check All Equation of Projectile Motion.

Horizontal velocity component: Vx = V * cos(α)
Vertical velocity component: Vy = V * sin(α)
Time of flight: t = 2 * Vy / g.
Range of the projectile: R = 2 * Vx * Vy / g.
Maximum height: hmax = Vy² / (2 * g)

Projectile Motion Equations Derivation

The derivation of the equations of motion for projectile motion involves analyzing the motion of an object that is launched into the air and follows a curved path under the influence of gravity, without any other forces like air resistance. Projectile motion can be broken down into horizontal and vertical motions, which are independent of each other. Here’s a step-by-step derivation:

Assumptions:

The only force acting on the projectile is gravity.
Air resistance is negligible.
The Earth’s surface is flat, and we neglect the curvature of the Earth.

Let’s consider a projectile launched from an initial position (x₀, y₀) with an initial velocity (v₀x, v₀y) at an angle θ above the horizontal axis.

Horizontal Motion: The horizontal motion of the projectile is uniform and is described by the equation: x = x₀ + v₀x * tWhere:
- x is the horizontal distance traveled by the projectile.
- x₀ is the initial horizontal position.
- v₀x is the initial horizontal velocity.
Since there are no horizontal forces (assuming no air resistance), the horizontal velocity (v₀x) remains constant throughout the motion.
Vertical Motion: The vertical motion of the projectile is affected by gravity. The equations of motion for vertical motion under gravity are:
- y = y₀ + v₀y * t – (1/2) * g * t²
- v = v₀y – g * t
Where:
- y is the vertical height above the initial position.
- y₀ is the initial vertical position.
- v₀y is the initial vertical velocity.
- g is the acceleration due to gravity (approximately 9.81 m/s²).
Time of Flight: The time it takes for the projectile to reach the ground (when y = 0) can be determined using the vertical motion equation: 0 = y₀ + v₀y * t – (1/2) * g * t²This is a quadratic equation in t, and you can solve for t using the quadratic formula.
Range (Horizontal Distance): The range (R) of the projectile is the horizontal distance it travels before hitting the ground. You can calculate it using the horizontal motion equation: R = x – x₀Substitute the expression for x from the horizontal motion equation.
Maximum Height: The maximum height (H) reached by the projectile is the highest point it reaches along the vertical path. You can find it by analyzing the vertical motion equation: v = v₀y – g * tAt the maximum height, the vertical velocity v becomes zero. Solve for t and then use it to find H from the vertical motion equation.

These derivations provide a complete set of equations to describe the motion of a projectile launched with an initial velocity at an angle to the horizontal axis under the influence of gravity.

Projectile Motion Formula

In the absence of extraneous forces, a ballistic trajectory is a parabola with homogenous acceleration, such as in a spaceship with constant acceleration. On Earth, the amplitude and direction of acceleration change with altitude and latitude/longitude. On a small scale, this results in an elliptic trajectory that is remarkably similar to a parabola. If an object were thrown and the Earth was replaced with a black hole of similar mass, it would be clear that the ballistic trajectory is part of an elliptic orbit around the black hole, not a parabola that continues to infinity. The trajectory can be circular, parabolic, or hyperbolic at higher speeds (unless distorted by other objects like the Moon or the Sun).

Projectile Motion Formula for Acceleration

The velocity in the horizontal plane is static, equal to v 0 cos, because there is only acceleration in the vertical plane. The projectile’s vertical motion is the motion of a particle in free fall. The acceleration is constant in this case, equal to g. The following are the components of the acceleration:

$a x = 0, a y = - g$

Projectile Motion Formula for Velocity

The magnitude of velocity (as determined by the Pythagorean theorem, often known as the triangle rule) is as follows:

$v={\sqrt {v_{x}^{2}+v_{y}^{2}}}$

Projectile Motion Formula for Displacement

At any time $(t )$ , the projectile’s displacements(x and y) in horizontal and vertical planes are given by:

$x = v 0 t cos ( θ ) ,$

y = v 0 t sin ( θ ) - 1/ 2 g t 2

The magnitude of the displacement is:

\Delta r={\sqrt {x^{2}+y^{2}}}

Projectile Motion Formula for Maximum Height of Projectile

For the displacement of the projectile’s greatest height:

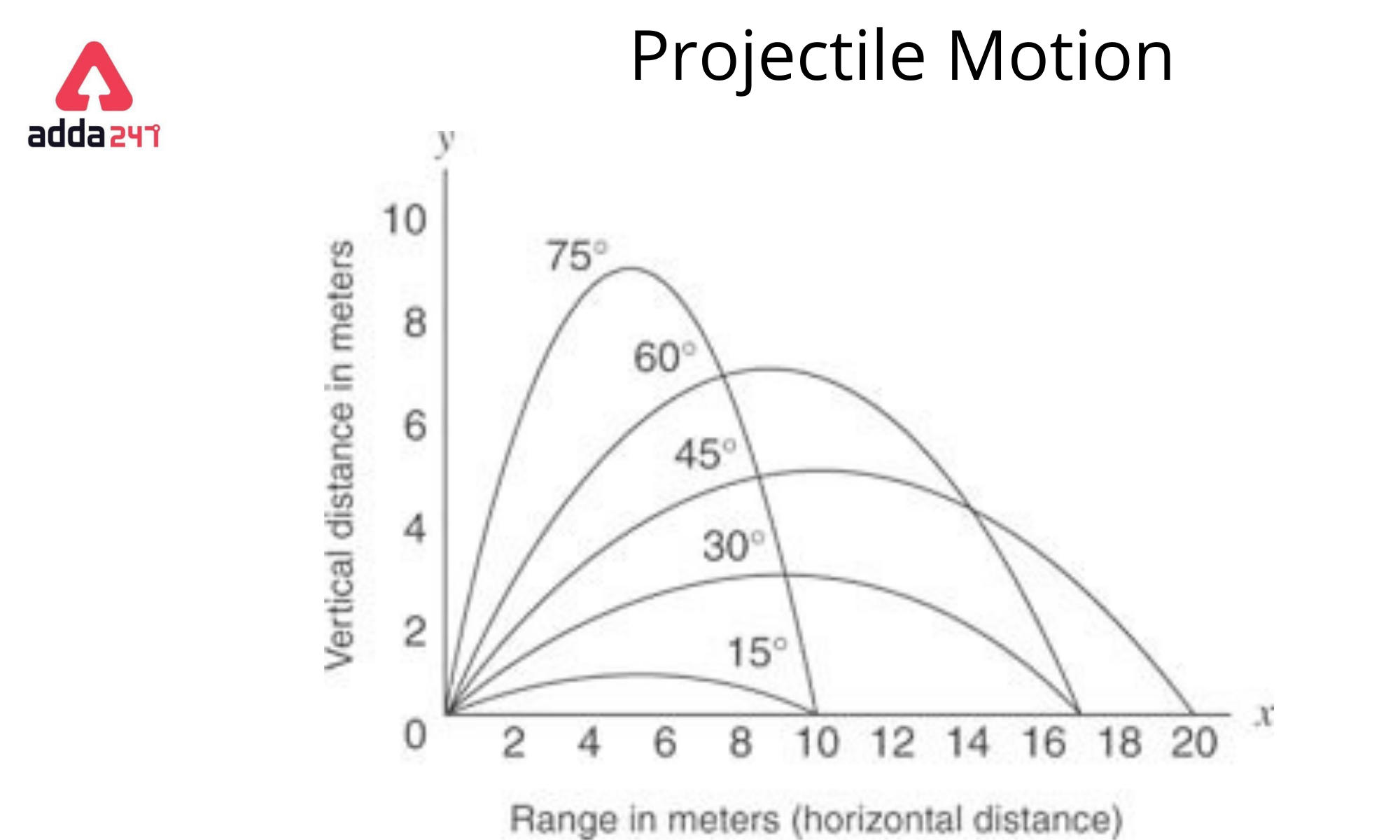
h = v₀ t_h sinθ – 1/2 g t_h²=> h = (v₀² sin²θ) / 2g

For θ=90°, the maximum achievable altitude is attained and is given by :

h = (v₀²) / 2g

Projectile Motion Formula Derivation

The derivation of the formula for projectile motion involves analyzing the motion of an object that is launched into the air and moves under the influence of gravity, without any other horizontal forces acting on it. Projectile motion can be divided into two components: horizontal motion and vertical motion. Here’s a step-by-step derivation of the formulas for projectile motion:

Define your coordinate system:
- Choose a coordinate system with a horizontal axis (x-axis) and a vertical axis (y-axis).
- Typically, the positive x-axis is chosen to be horizontal and the positive y-axis is chosen to be vertically upward.
- Define the initial position of the projectile (x₀, y₀) and the initial velocity (v₀) at an angle (θ) with respect to the horizontal axis.
Break the initial velocity into its horizontal and vertical components:
- The horizontal component of velocity (v₀x) is given by: v₀x = v₀ * cos(θ)
- The vertical component of velocity (v₀y) is given by: v₀y = v₀ * sin(θ)
Describe the motion along each axis:Horizontal Motion (x-axis):
- There are no horizontal forces acting on the projectile, so the horizontal velocity (v₀x) remains constant throughout the motion.
- The horizontal distance traveled (x) is given by: x = x₀ + v₀x * t
Vertical Motion (y-axis):
- The only force acting on the projectile along the y-axis is gravity (acceleration due to gravity is denoted as “g”).
- The vertical velocity (v_y) changes due to gravity:
  - v_y = v₀y – g * t
- The vertical position (y) is given by: y = y₀ + v₀y * t – (1/2) * g * t²
Determine the time of flight (T):
- The time it takes for the projectile to reach its maximum height (where v_y = 0) can be found by solving for t in the equation v_y = v₀y – g * t:
  - 0 = v₀y – g * t
  - t = v₀y / g
- The total time of flight (T) is twice this time because it takes the same amount of time to reach the maximum height and return to the same vertical position:
  - T = 2 * (v₀y / g)
Find the range (R) of the projectile:
- The range is the horizontal distance traveled by the projectile, which occurs when the projectile returns to the same vertical position it started from (y = y₀).
- Substitute T/2 for t in the horizontal motion equation: x = x₀ + v₀x * t
  - R = x₀ + v₀x * (T/2)
- Using the expressions for v₀x and T from earlier, you can write the range formula as:
  - R = (v₀² * sin(2θ)) / g

These are the fundamental equations for projectile motion. Depending on the specific problem, you can use these equations to analyze various aspects of the motion, such as the maximum height, time of flight, or range of the projectile.

Projectile Motion Examples for Class 11

Projectile Motion Example- Bullet shot by a gun

Because of the force supplied by the ignition of the gunpowder, a bullet shot from a gun travels a long distance. However, as soon as the bullet leaves the gun, gravity acts on it, causing it to follow a parabolic route and finally fall to the ground unless and until it is stopped by an opposing force.

Projectile Motion Examples- Cannonball Motion

You’ve probably seen historical footage of wars where cannon cannons were utilised. A cannon is a huge tubular weapon that fires projectiles. The calculations are made based on the projectile’s force and weight in order for the projectile to hit the intended target. Catapults are another example of a comparable device. The trebuchet, which uses a long arm to launch projectiles over large distances, is a well-known example of a catapult.

Projectile Motion Examples- The trajectory of a Baseball

In a baseball game, The bat hits the ball, which is then sent into the air. If you look closely, you’ll notice that the ball does not go in a round direction. Depending on the angle at which it is launched, the path is likely to be parabolic.

Projectile Motion Examples- The trajectory of a Javelin

A javelin is thrown to its maximum distance in a javelin throw game. This is similar to the hammer throw, but instead of running a short distance to gain momentum, the person throws the javelin. The javelin travels a predetermined distance before falling down in a parabolic direction. The angle of the throw is critical because it dictates how far the javelin travels. Wind parameters such as wind speed and direction are also important because they can alter the projectile’s velocity.

Projectile Motion Examples- The trajectory of water from a Pipe

You’ve probably seen water moving through a hose pipe, especially a high-pressure hose pipe. The water does not immediately fall to the earth, but instead follows a parabolic route. This is important for directing the flow of water so that it only falls on the specified area.

Related Post: