Polynomial- Definition, Formula, Types, Example

Table of Contents

Polynomial Definition

A polynomial is a mathematical equation made up of indeterminates (also known as variables) and coefficients and involving only addition, subtraction, multiplication, and non-negative integer exponentiation of variables. x2 4x + 7 is an example of a polynomial of a single indeterminate x. x3 + 2xyz2 yz + 1 is a three-variable example.

Polynomials

Polynomials can be found in a variety of fields of mathematics and science. For example, they are used to encode a wide range of problems, from simple word problems to complex scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used to approximate other functions in calculus and numerical analysis.

What is a Polynomial?

A polynomial is a mathematical expression consisting of variables (also known as indeterminates) raised to non-negative integer powers, combined through addition, subtraction, and multiplication by constants. In simpler terms, a polynomial is a sum of terms, where each term consists of a coefficient multiplied by one or more variables raised to non-negative integer exponents.

The general form of a polynomial is:

$P (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{2} x^{2} + a_{1} x + a_{0}$

Here:

$P (x)$ represents the polynomial as a function of $x$ .
$x$ is the variable.
$n$ is the highest non-negative integer exponent (degree) in the polynomial.
$a_{n}, a_{n - 1}, \dots, a_{2}, a_{1}, a_{0}$ are constants called coefficients.

Polynomials can have various degrees, and they are classified based on their degrees:

Constant Polynomial: Degree 0 (e.g., $P (x) = 5$ ).
Linear Polynomial: Degree 1 (e.g., $P (x) = 3 x - 2$ ).
Quadratic Polynomial: Degree 2 (e.g., $P (x) = 2 x^{2} + 5 x + 1$ ).
Cubic Polynomial: Degree 3 (e.g., $P (x) = x^{3} - 3 x^{2} + 2 x$ ).
Quartic Polynomial: Degree 4.
Quintic Polynomial: Degree 5.

Polynomials are fundamental in mathematics and have applications in various fields including algebra, calculus, geometry, physics, engineering, and computer science. They are used to model and solve a wide range of mathematical and real-world problems.

Polynomial Formula

A polynomial in a single indeterminate $x$ can always be written (or rewritten) in the form

a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0},

where $a_{0},\ldots ,a_{n}$ are constants that are called the coefficients of the polynomial, and $x$ is the indeterminate. The word “indeterminate” means that $x$ represents no particular value, although any value may be substituted for it. The mapping that associates the result of this substitution to the substituted value is a function, called a polynomial function.

This can be expressed more concisely by using summation notation:

\sum _{k=0}^{n}a_{k}x^{k}

That is, a polynomial can either be zero or can be written as the sum of a finite number of non-zero terms. Each term consists of the product of a number – called the coefficient of the term – and a finite number of indeterminates raised to nonnegative integer powers.

Polynomials Types

Polynomials are classified according to the number of words they contain. There are polynomials with one, two, three, and even more terms. Polynomials are classed as follows based on the number of terms:

Monomials: A monomial is a polynomial expression with a single term. For instance, 4z, 6x, 2x, and 18p. Furthermore, 8x + 9x + 5x is a monomial since it is made up of like elements that add up to 22x.
Binomials: They are polynomials that have two dissimilar terms. 8x + 4×9, for example, is a binomial because it contains two dissimilar components, 83x and 4×9 and 10pq + 13p2.
Trinomials: They are polynomials that have three dissimilar terms. 2x + 9×5 – 6×3 and 22pq + 8×2 – 10 are two examples.

Also,

The degree of the polynomial is the power of the leading term or the highest power of the variable. This is accomplished by placing the polynomial terms in ascending order of power. They can be divided into four categories based on the degree of the polynomial. They are, indeed Zero polynomial, Linear polynomial, Quadratic polynomial, Cubic polynomial

Polynomial Function

A polynomial function is one that uses only non-negative integer powers or positive integer exponents of a variable in an equation such as the quadratic equation or the cubic equation. 2x+5 is a polynomial with an exponent of one, for example.
In general, a polynomial function is often referred to as a polynomial or polynomial expression, depending on the degree of the function. The highest power found in a polynomial is its degree. In this article, you will learn about polynomial functions, including zero, one, two, and higher degree polynomials, as well as their expressions and graphical representations.

Examples of Polynomials for Class 9

Here are some examples of polynomials:

Constant Polynomial (Degree 0):
$P (x) = 7$

This is a polynomial with a constant term. It doesn’t involve any variable $x$ and has a degree of 0.
Linear Polynomial (Degree 1):
$P (x) = 3 x - 5$

This is a linear polynomial with a degree of 1. It has one term involving the variable $x$ raised to the first power.
Quadratic Polynomial (Degree 2):
$P (x) = 2 x^{2} + 4 x + 1$

This is a quadratic polynomial with a degree of 2. It has terms involving $x^{2}$ , $x$ , and a constant term.
Cubic Polynomial (Degree 3):
$P (x) = x^{3} - 2 x^{2} + 5 x - 3$

This is a cubic polynomial with a degree of 3. It has terms involving $x^{3}$ , $x^{2}$ , $x$ , and a constant term.
Quartic Polynomial (Degree 4):
$P (x) = 4 x^{4} + x^{3} - 2 x^{2} + 7 x - 1$

This is a quartic polynomial with a degree of 4. It has terms involving $x^{4}$ , $x^{3}$ , $x^{2}$ , $x$ , and a constant term.
Polynomial with Fractional Coefficients:
$P (x) = 2 1 x^{2} - 4 3 x + 8 1$

This polynomial has fractional coefficients. It’s a quadratic polynomial with a degree of 2.

These examples demonstrate different types of polynomials based on their degrees and coefficients. Polynomials can have various forms and are used to model a wide range of mathematical and real-world situations.

Related Post:

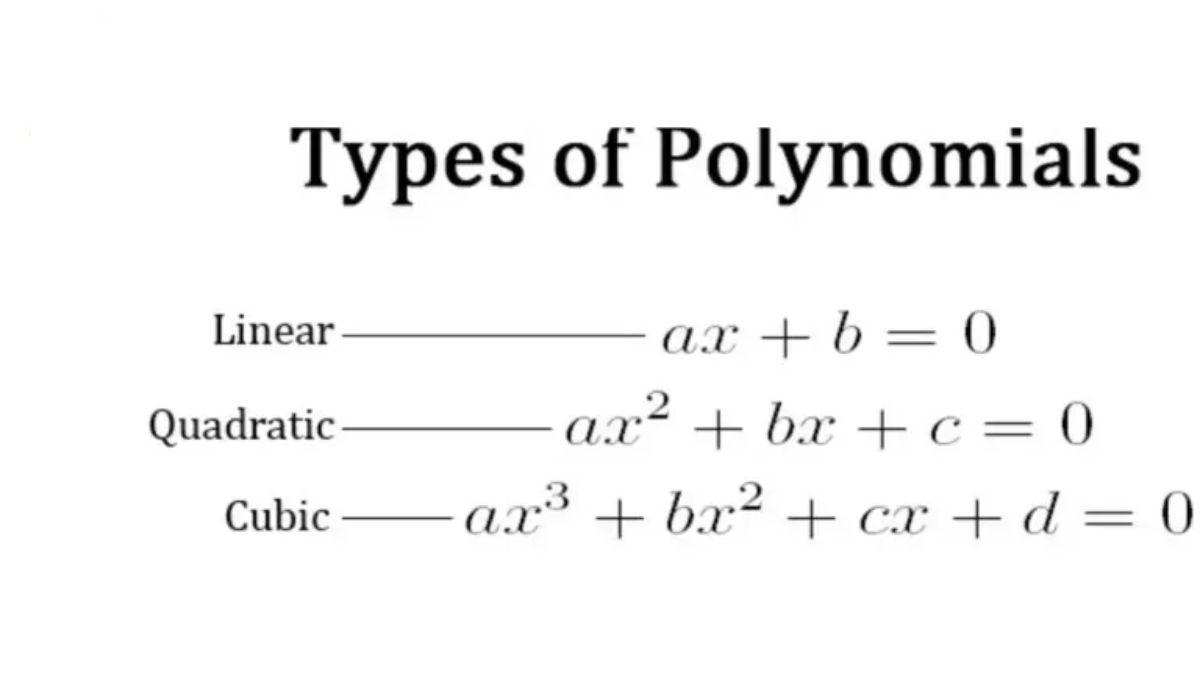
Polynomials Class 9 & 10 QNAs

Ques. What is a polynomial with example?

Ans. Polynomials are sums of terms of the form kxn, where k is any positive integer and n is any number. 3x+2x-5, for example, is a polynomial. Polynomials are a type of polynomial. The phrases terms, degree, standard form, monomial, binomial, and trinomial are all covered in this video.

Ques. How do you identify a polynomial?

Ans. A polynomial of the form ? + ? ? + ? ? + ⋯ + ? ? . … .The value of the variable’s exponent is the degree of a monomial. A sum of monomials is a polynomial. The highest degree of a polynomial’s monomials is its degree.

Ques. What are polynomial terms?

Ans. Polynomial terms are the components of the equation that are usually separated by “+” or “-” signs. As a result, each term in a polynomial equation is a part of the polynomial. The number of terms in a polynomial like 8x² + 9 +4 is 3, for example.

Ques. What is coefficient in polynomial?

Ans. The coefficient is the result of multiplying a number by a variable. The variable x is the variable, while the coefficient 12 is the coefficient.

Ques. What is meant by zero polynomial?

Ans. The constant polynomial has all of its coefficients equal to 0. The constant function with value 0 (also known as the zero map) is the analogous polynomial function. The additive identity of the additive group of polynomials is the zero polynomial.

Ques. Why is polynomial important?

Ans. Polynomials are an important aspect of mathematics and algebra’s “language.” They are used to express numbers as a result of mathematical operations in almost every branch of mathematics. Other sorts of mathematical expressions, such as rational expressions, use polynomials as “building blocks.”