Slope Formula
To calculate the steepness or inclination of the line we use the slope formula. The slope line shows how inclined the line is and to calculate the slope of lines we use the x and y coordinate of the line. The change in the y-axis ratio change in the x-axis is equal to the slope of the line.
Slope Formula in Maths
The students find maths really difficult to understand they just ignore maths problems. To ease students who are facing issues in the topic of Slope Formula, we have come up with this article to make students understand the slope formula in layman’s language. In this article, we have covered the slope formula and solved examples of slope formulas. Students must bookmark this page to get updates about related articles. We are updating many related topics on a daily basis.
Slope Formula of Line in (Graphs) Maths & Coordinate Geometry
The slope formula is used to calculate the steepness of the line, in this formula the slope is computed as the change in y-axis ratio change in the x-axis. The computed slope will be zero if the line neither rises nor falls. The slope of the line will be defined as the line’s angle of inclination from the horizontal whether the slope rises or falls. The zero slopes occur when the horizontal lines neither rise nor fall which means the line extends to infinity in the left or right of the axis. The points in the coordinate geometry represent as a coordinate value. These points are found on the x-axis and y-axis, i.e. (x,y) represents the points on the geometric plane. Whereas the (0, 0) points represented the origin point of the coordinate.
Formula for Slope
The formula for calculating the slope of a line in a Cartesian coordinate system (i.e., a straight line on a graph) is given by:
In this formula:
represents the slope of the line.
and
are the coordinates of two points on the line.
is the change in the y-coordinates (the vertical change) between the two points.
is the change in the x-coordinates (the horizontal change) between the two points.
You can use this formula to find the slope of a line when you know the coordinates of two points on that line.
Slope Formula Calculator
Let’s derive the formula of the slope with the definition given above.
| m = (y2-y1)/(x2-x1) |
Where,
x1 and x2 are the coordinates of the x-axis.
y1 and y2 are the coordinates of the y-axis.
m = slope of the line.
In the above formula, the numerator contains the difference of the points that exist on the y-axis, the points are y1 and y2. whereas the denominator contains the difference of the points that exist on the x-axis, the points are x1 and x2.
Slope of Line Formula
We only need two points from a line to find its slope: (x1, y1) and (x2, y2) (x2, y2). The slope of a straight line can be calculated in three steps.
Step 1: Find the two points on the line.
Step 2: Identify one point to be (x1,y1)
Step 3: Identify another point to be (x2,y2).
Step 4: Use the slope formula given above to calculate the slope.
Derivation of Slope Formula
We can derive the slope formula easily. The x and y coordinates of the line are used to calculate the slope formula of the line. The net change in the y coordinate is Δy, while the net change in the x coordinate is Δx. So the change in the y coordinate with respect to the change in the x coordinate can be written as,
m = Δy/Δx
where the parameters are,
- m is the slope
- Δy is the change in y-coordinates
- Δx is the change in the x-coordinates
We know in case of Scope that tan θ is also the slope of the line where θ is the angle made by the line with the positive direction of the x-axis.
And, tanθ = height/base
Since the height/base between any two given points = (y2 – y1)/(x2 – x1)
Thus, the slope equation is, m = tanθ = Δy/Δx
From the graph, we observe:
- Δy = (y2 – y1)
- Δx = (x2 – x1)
Thus, the slope formula is given as: Slope = m = (y2 – y1)/(x2 – x1) Hence Proof.
Equation for Slope
As we discussed in the previous section, the slope formula can be used to determine the slope of any line. The slope equation that can be used in finding this slope can therefore be written as given below,
m = rise/run = tanθ = Δy/Δx = (y2 – y1)/(x2 – x1)
where,
- m is the slope
- Δy is the change in y-coordinates
- Δx is the change in the x-coordinates
- θ is the angle made by the line with the positive x-axis
Also, the equation of slope of any line using the line equation can be given as,
y = mx + b
where,
- m is the slope of the line
- b is the y-intercept of the line
Gradient Formula
The gradient is a vector that points in the direction of the steepest increase of a function. It is represented as ∇ (pronounced “nabla”) followed by the function it operates on. The gradient of a scalar function f(x, y, z) in three-dimensional space is given by:
∇f = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k
Here, ∇f represents the gradient of the function f, and i, j, and k are the unit vectors along the x, y, and z axes, respectively. The partial derivatives (∂f/∂x), (∂f/∂y), and (∂f/∂z) represent the rate of change of the function in the x, y, and z directions, respectively.
In a more general form, if you have a scalar function f defined in n-dimensional space, the gradient is given as:
∇f = (∂f/∂x₁)i₁ + (∂f/∂x₂)i₂ + … + (∂f/∂xₙ)iₙ
Where x₁, x₂, …, xₙ are the coordinates in each dimension, and i₁, i₂, …, iₙ are the unit vectors along each dimension.
The gradient is a fundamental concept in vector calculus and is used in various fields, including physics, engineering, and machine learning, to optimize functions and understand the behavior of functions at specific points.
Formula for Slope Examples in Maths
Here we have given the solved examples of slope formula the students must try to solve the given questions without seeing their solutions, if unable to find the answer then refer to the given solution. Only mugging up concepts won’t work in the final examination, since the board rarely asks questions from theory in maths, so it won’t help much. Thus, students are advised to practice as much as questions they can. Try to solve the questions given below:
Slope Formula Based Example 1: Find the slope of the line whose coordinates are (4,2) and (7,9)?
Solution:
We have,
(x1, y1) = (4,2)
(x2, y2) = (7,9)
slope of a line formula m = (y2 − y1) /( x2 − x1)
Put the values of x1, x2, y1, y2 in the above formula.
m = (9-2)/ (7-4)
m = 7/3
Here we have got the slope of line is 7/3.
Slope Formula Based Example 2: If the slope of a line passing through the points (2, a) and (4, 5) is 8, then what is the value of a?
Solution:
We have
Slope = m = 8
Points:
(x1, y1 ) = (2, a)
(x2, y2) = (4, 5)
We know that,
Slope (m) = (y2– y1 )/(x2– x1)
pull all the values in the slope formula given above
8 = 5-a/4-2
16 = 5-a
a = 5 – 16
a = -9
Therefore, the value of a = -9
Slope Formula Based Example 3: Find the slope of the line whose coordinates are (8, 6) and (9, 5)?
Solution:
We have,
(x1, y1) =(8, 6)
(x2, y2) = (9, 5)
slope of a line formula m = (y2 − y1) /( x2 − x1)
Put the values of x1, x2, y1, y2 in the above formula.
m = (5-6)/ (9-8)
m = -1/1
m = -1
Here we have got the slope of line is -1.
Slope Formula Based Example 4: If the slope of a line passing through the points (6, 2) and (7, x) is 4, then what is the value of x?
Solution:
We have
Slope = m = 4
Points:
(x1, y1 ) = (6, 2)
(x2, y2) = (7, x)
We know that,
Slope (m) = (y2– y1 )/(x2– x1)
pull all the values in the slope formula given above
4 = x-2/7-6
4 = x-2/1
4 = x-2
x = 6
Therefore, the value of x = 6
Slope Formula Based Example 5: Find the slope of the line whose coordinates are (7, 6) and (1, 4)?
Solution:
We have,
(x1, y1) = (7, 6)
(x2, y2) = (1, 4)
slope of a line formula m = (y2 − y1) /( x2 − x1)
Put the values of x1, x2, y1, y2 in the above formula.
m = (4-6)/ (1-7)
m = -2/(-6)
m = 1/3
Here we have got the slope of line is 1/3.
Slope Formula Based Example 6: If the slope of a line passing through the points (9, y) and (5, 2) is 4, then what is the value of y?
Solution:
We have
Slope = m = 4
Points:
(x1, y1 ) = (9, y)
(x2, y2) = (5, 2)
We know that,
Slope (m) = (y2– y1 )/(x2– x1)
pull all the values in the slope formula given above
4 = 2-y/5-9
4 = 2-y/(-4)
-16 = 2-y
y = 2+16
y = 18
Therefore, the value of y = 18
Related Posts:

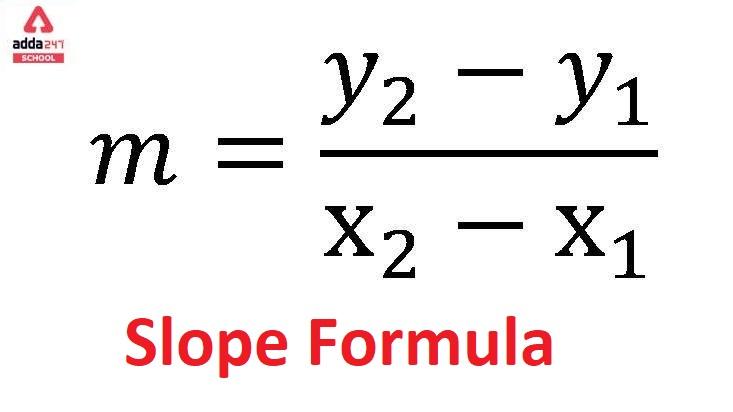







 CUET BHU Cut off 2025: Course-wise and C...
CUET BHU Cut off 2025: Course-wise and C...
 DAVV Result 2025 Out, Download Devi Ahi...
DAVV Result 2025 Out, Download Devi Ahi...
 Calicut University Timetable 2025 PDF Re...
Calicut University Timetable 2025 PDF Re...










