How to find the mode for a given set of values?

If we have a set of values equal to 2, 4, 5, 6, 2, 7, 2. Then the most repeated value in the given set is 2. Therefore, mode of the given set is 2.

Can there be two modes in a given set of data?

Yes, a given set of data can contain two modes such modes are known as bimodal modes.

What is trimodal mode?

If a given set of data has three modes then these modes are known as a trimodal mode.

What is multimodal mode?

If the given set of data has four or more than four modes then such modes are known as multimodal modes.

What is no mode condition?

It is considered to be no mode if the given set of data has no value that is repeated in the set more than once.

Mode Formula with Example -

Table of Contents

Mode Meaning and Definition

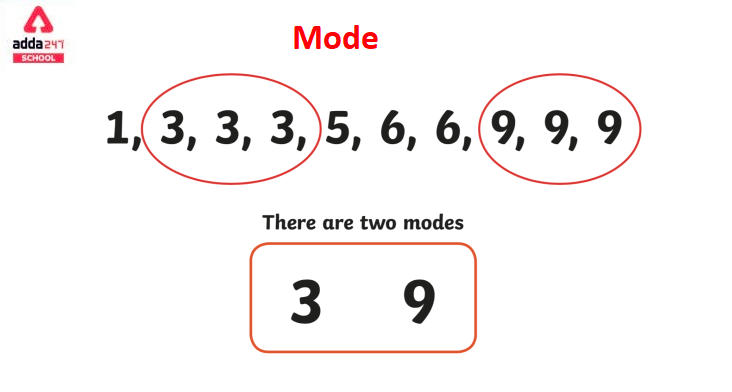
In Statistics, the mode is a set of data or observations that occurs multiple times. The mode has the highest frequency of occurrence in the given set of data. The given set of data can have one mode or more than one mode, which means if two values are repeating with the same frequency then we call the mode of the given set of data. If a given set of data has one mode then it’s called unimodal, if it has two modes then it’s called bimodal, if it has three modes then it’s called trimodal, if the data has more than four or four modes then we called it multimodal.

Mode Formula

The mode is a statistical measure that represents the most frequently occurring value or values in a data set. It’s used to describe the central tendency of a data set and can be particularly useful when dealing with categorical or discrete data. There can be one mode (unimodal), multiple modes (multimodal), or no mode at all in a data set.

The Mode Formula for finding the mode depends on the type of data you are working with:

Mode Formula For UnGrouped Data

If you have a list of individual data points, you can find the mode by simply identifying the value(s) that appear most frequently in the dataset.

Mode Formula For Grouped Data

If you have grouped data (data divided into intervals or classes), finding the mode is slightly different. In this case, you identify the modal class, which is the interval or class with the highest frequency. You can estimate the mode within that class.

For grouped data, the Mode Formula to estimate the mode within the modal class is:

Mode ≈ L + [(f1 – f0) / (2f1 – f0 – f2)] * C

Where:

- L is the lower boundary of the modal class.
- f1 is the frequency of the modal class.
- f0 is the frequency of the class immediately before the modal class.
- f2 is the frequency of the class immediately after the modal class.
- C is the width of the class interval.

Mode Formula’s important to note that the mode may not always be applicable or meaningful for all types of data. Additionally, a dataset can have no mode (if all values occur with equal frequency) or multiple modes (if more than one value occurs with the highest frequency).

When calculating the mode, make sure to properly identify whether you are dealing with raw data or grouped data, and apply the appropriate formula accordingly.

Mode of Grouped Data with Two Highest Frequency

To find the mode of grouped data with the two highest frequencies, you can follow these steps:

Calculate the midpoint for each class interval in the grouped data.
Find the frequency and the corresponding class intervals.
Identify the two class intervals with the highest frequencies.
Calculate the mode(s) for these two class intervals.

Here’s a step-by-step example:

Suppose you have the following grouped data:

Class Interval	Frequency
10 – 20	8
20 – 30	15
30 – 40	12
40 – 50	18
50 – 60	22

Step 1: Calculate the midpoints for each class interval:

Midpoint of 10 – 20: (10 + 20) / 2 = 15
Midpoint of 20 – 30: (20 + 30) / 2 = 25
Midpoint of 30 – 40: (30 + 40) / 2 = 35
Midpoint of 40 – 50: (40 + 50) / 2 = 45
Midpoint of 50 – 60: (50 + 60) / 2 = 55

Step 2: Identify the two class intervals with the highest frequencies. In this case, the two highest frequencies are 22 and 18.

Step 3: Find the mode(s) for these two class intervals.

For the class interval 50 – 60 (frequency = 22): The mode for this class interval is the midpoint, which is 55.

For the class interval 40 – 50 (frequency = 18): The mode for this class interval is also the midpoint, which is 45.

So, in this example, there are two modes: 55 and 45, which correspond to the class intervals 50 – 60 and 40 – 50, respectively, as they have the two highest frequencies.

Mode Formula in Statistics (Maths)

Let’s learn with the example, we have given an example below, where we have given the score of a cricket match along with the score we have given the number of balls.

Number of Balls	1	2	3	4	5	6	7	8	9
Runs	1	2	4	6	2	1	4	6	4

In the above example, the number 4 is repeated 3 times and which is the highest frequency of the data given in the table. That means only number 4 repeated 3 times, no other number repeated 3 times. So, we have learned above the definition of mode, through the definition of mode the above example has only one mode which is 4, and the data which has only one mode is called unimodal.

Types of Mode in Maths/Statistics

There are four types of modes which are unimodal, bimodal, trimodal, and multimodal. Let us understand these modes with the help of an example:

Unimodal Mode Formula

If the set of given data or observations contains only one mode then this mode is known as a unimodal mode.

Example: If the given set of data is X = { 2, 10, 14, 10, 12, 10, 8, 3, 2, 10, 2, 9}

In the data set 10 has the highest frequency then it can be called the unimodal data set.

Bimodal Mode formula

If the set of given data or observations contains only two modes then this mode is known as a bimodal mode.

Example: If the given set of data is X = { 2, 1, 2, 10, 1, 1, 8, 3, 2, 1, 2, 9}

In the data sets, 2 and 1 have the highest frequency then it can be called the bimodal data set.

Trimodal Mode Formula

If a data set or observation has three modes then it’s called trimodal mode. If the data set has 3 values that are repeating with the same frequency that you can say that the given data set has three modes.

Example: If the given set of data is X = {11, 12, 11, 13, 10, 9, 12, 13, 8, 7, 1, 2, 4}

In the example above, the numbers 11, 12, and 13 are repeated with the same frequency and have the highest frequency among other numbers. Hence, it is called a trimodal data set.

Multimodal Mode

If a given set of data has more than four or four modes is called multimodal mode. Let us understand multimodal mode with an example

Example: Given a set of data Y = {2, 3, 5, 1, 2, 5, 6, 7, 4, 3, 1, 4, 7}

The above example has 5 modes then these modes are called multimodal modes. All 5 modes are repeating with the same frequency.

unimodal, bimodal multimodal examples

Unimodal, Bimodal, Multimodal Mode Formula with Example

In statistics and data analysis, the term “mode” refers to the value or values that appear most frequently in a dataset. Modes can be categorized into three main types: unimodal, bimodal, and multimodal. Let’s explore each of these with examples:

Unimodal:
- Unimodal distributions have a single peak or mode.
- In a unimodal distribution, there is one value that occurs more frequently than any other.
- Example: The heights of adult humans in a given population are often unimodal, with the mode around the average height.
Bimodal:
- Bimodal distributions have two distinct peaks or modes.
- In a bimodal distribution, there are two values that occur more frequently than others, creating two distinct peaks in the data.
- Example: In a survey of students’ favorite ice cream flavors, you might find that chocolate and vanilla are the two most popular flavors, creating a bimodal distribution.
Multimodal:
- Multimodal distributions have more than two distinct peaks or modes.
- In a multimodal distribution, there are three or more values that occur more frequently than others, resulting in multiple peaks in the data.
- Example: The distribution of scores on a complex exam might be multimodal, with peaks corresponding to students who performed exceptionally well, those who performed moderately, and those who performed poorly.

It’s important to note that the number of modes in a dataset is not fixed, and it depends on the characteristics of the data. Some datasets may not exhibit any clear modes, while others may have more than three modes if the data is particularly complex or diverse. Modes are just one way to describe the central tendency of a dataset, and they can provide insights into the distribution of values within it.