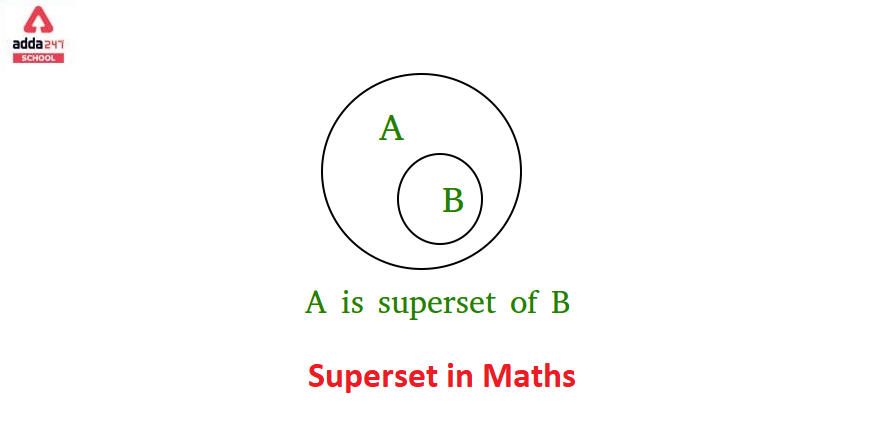
Superset Meaning, Definition, Examples in Maths

Superset Meaning & Definition

Superset can be called the set of any another if all the other rudiments of the other set are rudiments of this set. Let us understand this conception by way of an illustration, if an X lies inside Y, also we can know that Y contains X. It also means that X is a subset of Y, and also we can say Y is a superset of X. The superset relation between Set X and Set Y can be denoted as X ⊃Y. Suppose say Set X has the ensuing rudiments{ c, d, e, f, g, h, i, j} and Set Y has{ g, h, i, j}. also we can say that X ⊃Y. In case some or all of the rudiments in Set Y are the rudiments of set X, also Set Y will be considered as the Superset of X.

Difference Between Subset and Superset

Subset and Superset are different from each other. Students get confused between them both very often. A Subset and Superset are the opposite of each other. However, also Set X is said to be a subset of Set Y, If elements of Set X are said to be contained in Set Y. By taking an example let us understand Subset and Superset. Say Set X consists{a,b,c,d,} and Set Z consists{a,b}, in this case, we can say that Set Z is a subset of Set X and Set X is a superset of Set Z.

Properties of a Superset

The properties  of a Superset are bandied below

1. A Superset is a superset of an empty set
2. Each set is the SuperSet in itself
3. There are a horizonless number of Superset of a Set. still, also similar to another set is the Superset of that set, If any set is said to be the Subset of another set, for example, A is the subset of C, and also C is the Superset of A.
4. A null set doesn’t contain any other element, so we can say that each set is the Superset of a null set.

Superset Definition in Maths

A Proper Superset is also known as a strict Superset. Set X can be said to be the proper Superset of Y when all rudiments of Set Y are in Set X, and Set X must contain at least one element of Set Y. Let us take an illustration to understand this concept well. Set A = { a, b, c}, Set B = { a, b, c, d, e}, Set C consists{ a, b, c} and Set D{a.b.h}. also, in this case, we can find that Set B is the Superset of set A and Set B isn’t equal to SetA. Set C is the Superset of Set A, but Set C isn’t a proper superset of set A. D isn’t a superset of A, as set D doesn’t contain the element c, which is present in Set A.

Superset Examples

Q1. You are asked to check whether the Real Number is a superset of the following sets given below:

1. Natural Numbers
2. Whole Numbers
3. Integers
4. Rational Numbers
5. Irrational Numbers
6. Complex Numbers

Answer: The collection of factual figures R is the product of the sets of rational figures( Q) and illogical figures( Q’). As a result, the set of real figures, R = Q Q’. This also implies that real figures contain natural figures, whole figures, integers, rational figures, and illogical figures. Going by this, the answer is

R( Real figures) ⊃ N( Natural figures)

R( Real figures) ⊃ W( Whole figures)

R( Real figures) ⊃ Z( Integers)

R( Real figures) ⊃ Q( Rational figures)

R( Real figures) ⊃ Q'( Irrational figures)

As a result, the set R, which is the set of real figures, is the Superset of natural figures, whole figures, integers, rational figures, and illogical figures. On the other hand, complex figures are neither rational nor illogical and hence aren’t real figures; thus, the set of real figures can not be nominated as the Superset of the set of complex figures C. This suggests that C R. As a result, R isn’t the Superset of complex figures.

Q 2. Set A consists of{ a, b, c, d, e, f, z} and set B consists of{ a, e, I, o, u}. Identify the Superset and the subset.

Answer: handed, Set A = a, b, c, d, e, f,. z, i.e. all the English rudiments, and Set B = a, e, I o, you, i.e. all the five vowels that are simply set up in English rudiments. As a result, we may conclude that set A is the Superset of subset B,i.e. AB.

Q3. Determine if the following assertions are true or untrue.

a) An empty set is a superset of all sets.

b) Each set is a subset of the empty set.

c) All sets are supersets of themselves.

d) There are a finite number of supersets for each set.

Answer: The following are the rates of a superset

a) False

b) True

c) True

d) False

Related Posts:

• Standard Meridian Of India
• Why Is India Called A Subcontinent? For Class 9
• Difference Between Plant Cell And Animal Cell For Class 9
• ICSE Full Form
• Tribhuj Ka Kshetrafal (त्रिभुज का क्षेत्रफल)- Formula, Sutra
• Area Of A Triangle- Formula In Class 10 Co-Ordinate Geometry
• Electrochemical Series Of Metals- NCERT, Trick, Order Class 11 & 12
• Herbs Plant Examples, Definition, With Names
• Atal Tunnel Rohtang: Lenght, Weather, Map, Temperature Today
• Adverb Definition And Examples, Meaning And Types

Superset Meaning, Definition, Examples in Maths- FAQs

Q1. What is a Superset?

Answer: Superset can be the set of any other set if all the other elements of the other set are elements of this particular set. For example,  if  X lies inside Y, then we can say that Y contains X. It also means that X is a subset of Y, and then we can say Y is a superset of X. The superset relation between Set X and Set Y can be denoted as X⊃Y. Suppose say Set X has the following elements {c,d,e,f,g,h,i,j} and Set Y has {g,h,i,j}. Then we can say that X⊃Y.

Q2. What is the difference between Subset and Superset?

Answer: Subsets and Supersets are basically the opposite of each other. If elements of Set X are said to be contained in Set Y, then Set X is can be a subset of Set Y. Say Set X consists {2,3,4,5,6,7,8,} and Set Z consists {5,6,7}, in this case, we can say that Set Z is a subset of Set X and Set X is a superset of Set Z.

Q3. What is a Proper Superset?

Answer: A Proper Superset can also be called a strict Superset. Set X will be said to be a  proper Superset of Y when all the elements of Set Y are in Set X, and Set X must contain at least one element of Set Y.

Sharing is caring!