Tribhuj ka Kshetrafal ( त्रिभुज का क्षेत्रफल )
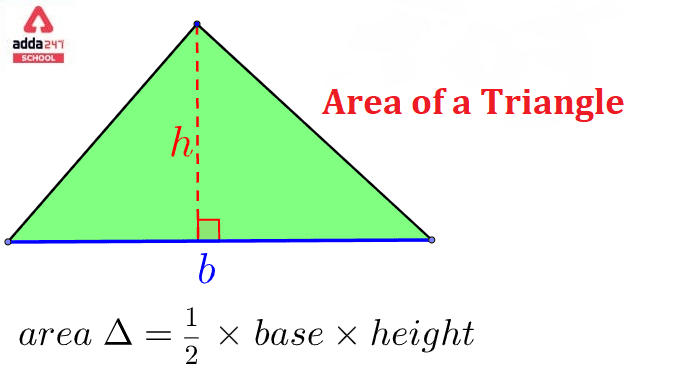
किसी त्रिभुज की तीनों भुजाओं से घिरा क्षेत्र त्रिभुज का क्षेत्रफल कहलाता है। सामान्य तौर पर, यह ऊंचाई के आधार गुणा के आधे के बराबर होता है, यानी A = 1/2 (bxh)। नतीजतन, त्रिकोणीय बहुभुज के क्षेत्र की गणना करने के लिए, हमें पहले आधार (बी) और ऊंचाई (एच) खोजना होगा। यह सभी प्रकार के त्रिभुजों पर लागू होता है, जिसमें स्केलीन, समद्विबाहु और समबाहु त्रिभुज शामिल हैं। यह देखा जाना चाहिए कि त्रिभुज का आधार और ऊँचाई एक दूसरे के लंबवत हैं। क्षेत्रफल की इकाई वर्ग इकाई (m2, cm2) में मापी जाती है। इस लेख में, हमने त्रिभुज के क्षेत्रफल, त्रिभुज के क्षेत्रफल की गणना करने की विधियों पर चर्चा की है। त्रिभुज के क्षेत्रफल की गणना करने का तरीका जानने के लिए बने रहें और पूरा लेख पढ़ें और सभी लेखों के नवीनतम अपडेट प्राप्त करने के लिए इस पृष्ठ को बुकमार्क करें।
Tribhuj ka Chetrafal- त्रिभुज का क्षेत्रफल
3 भुजाओं वाले त्रिभुज सूत्र का क्षेत्रफल
त्रिभुज के सूत्र की गणना करने के कई तरीके हैं। उदाहरण के लिए, जब हम दो भुजाओं और उनके बीच के कोण को जानते हैं, तो हम त्रिभुज के क्षेत्रफल की गणना के लिए त्रिकोणमितीय कार्यों का उपयोग कर सकते हैं। जब हम त्रिभुज की तीनों भुजाओं की लंबाई जानते हैं तो दूसरी विधि का उपयोग कर सकते हैं, हम त्रिभुज के क्षेत्रफल की गणना करने के लिए हीरोन के सूत्र को लागू कर सकते हैं। इसके अलावा, त्रिभुज के क्षेत्रफल की गणना के लिए मूल सूत्र है:
Are you in class12th/passed and willing to get admission in TOP COLLEGE of India ?
Fill up google form for the right guidance towards your GOAL
Tribhuj ka kshetrafal ka Sutra Barabar
त्रिभुज का क्षेत्रफल = A = ½ (b × h) वर्ग इकाई
यहाँ A = त्रिभुज का क्षेत्रफल
बी = त्रिभुज का आधार
एच = त्रिभुज की ऊंचाई
त्रिभुज का क्षेत्रफल सूत्र
त्रिभुज का क्षेत्रफल का सूत्र निम्नलिखित है:
(बेज * उचाई) / 2
यहाँ, बेज त्रिभुज के बुनियादी बेज को निर्दिष्ट करता है, जबकि उचाई त्रिभुज की उचाई को निर्दिष्ट करती है।
उदाहरण के लिए, यदि त्रिभुज का बुनियादी बेज 3 इंच और उचाई 4 इंच है, तो क्षेत्रफल: (3 * 4) / 2 = 6 सेंटीमीटर के बीज होगा।
Tribhuj ka kshetrafal ka sutra (त्रिभुज का क्षेत्रफल का सूत्र)
निर्देशांक ज्यामिति में त्रिभुज का क्षेत्रफल
यहां हमने सूत्रों का उपयोग करके त्रिभुज के क्षेत्रफल की गणना करने के तरीके दिए हैं। समद्विबाहु त्रिभुज, समबाहु त्रिभुज और समकोण त्रिभुज जैसे विभिन्न प्रकार के त्रिभुजों के क्षेत्रफल की गणना करने के सूत्र नीचे दिए गए हैं।
एक समद्विबाहु त्रिभुज का क्षेत्रफल
एक समद्विबाहु त्रिभुज की दो भुजाएँ बराबर होती हैं और समान भुजाओं के सम्मुख कोण भी समान होते हैं।
एक समद्विबाहु त्रिभुज का क्षेत्रफल = 1/4 b√(4a2 – b2)
जहाँ, b = त्रिभुज का आधार
a = दो बराबर भुजाओं में से किसी एक भुजा का माप
एक समकोण त्रिभुज का क्षेत्रफल
एक समकोण त्रिभुज, जिसे अक्सर समकोण त्रिभुज के रूप में जाना जाता है, में एक 90° कोण और दो 60° कोण होते हैं जो 90° तक जोड़ते हैं। नतीजतन, त्रिभुज की ऊंचाई लंबवत पक्ष की लंबाई के बराबर होती है।
एक समकोण त्रिभुज का क्षेत्रफल = A = 1/2 × आधार × ऊँचाई
यहाँ A = त्रिभुज का क्षेत्रफल
बी = त्रिभुज का आधार
एच = त्रिभुज की ऊंचाई
एक समबाहु त्रिभुज का क्षेत्रफल
एक समबाहु त्रिभुज वह होता है जिसकी सभी भुजाएँ बराबर होती हैं। त्रिभुज के शीर्ष से उसके आधार तक अनुरेखित लम्ब आधार को दो बराबर भागों में विभाजित करता है। एक समबाहु त्रिभुज के क्षेत्रफल की गणना करने के लिए, हमें पहले इसकी भुजाओं की लंबाई निर्धारित करनी चाहिए।
एक समबाहु त्रिभुज का क्षेत्रफल = A = (√3)/4 × भुजा2
यहाँ, A = त्रिभुज का क्षेत्रफल
भुजा = त्रिभुज की भुजा
Tribhuj ka Kshetrafal barabar- त्रिभुज का क्षेत्रफल: हल किए गए उदाहरण और सूत्र
Q.1: एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसका आधार 20 सेमी और ऊंचाई 10 सेमी है।
त्रिभुज का क्षेत्रफल = (1/2) × b × h
ए = 1/2 × 20 × 10
ए = 1/2 × 200
अत: एक त्रिभुज का क्षेत्रफल 100 सेमी2 है।
Q.2: एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसका आधार 6 सेमी और ऊंचाई 3 सेमी है।
त्रिभुज का क्षेत्रफल = (1/2) × b × h
ए = 1/2 × 6×3
ए = 1/2 ×18
अत: त्रिभुज का क्षेत्रफल 9 सेमी2 है।
Q.3: एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसका आधार 12 सेमी और ऊंचाई 16 सेमी है।
त्रिभुज का क्षेत्रफल = (1/2) × b × h
ए = 1/2 × 12 × 16
ए = 96
अत: त्रिभुज का क्षेत्रफल 96 सेमी2 है।
Q.4: 12 सेमी भुजा वाले एक समबाहु त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समबाहु त्रिभुज का क्षेत्रफल = A = (√3)/4 × (भुजा)2
समबाहु त्रिभुज की भुजा दी हुई है = 12cm
ए = (√3) / 4 × (पक्ष) 2
ए = (√3) / 4 × (12)2
ए = (√3) / 4 × 144
ए = 36√3 सेमी2
Related Post:
- Aryabhatta
- Mass of Electron, Proton, and Neutron in g, kg, mev, amu
- CCC Full Form – Course on Computer Concepts
- Longest Dam in India- Hirakud Dam
Tribhuj ka Kshetrafal (त्रिभुज का क्षेत्रफल)- Formula, Sutra- FAQs
Q. समबाहु त्रिभुज के क्षेत्रफल की गणना कैसे करें?
एक समबाहु त्रिभुज का क्षेत्रफल = A = (√3)/4 × (भुजा)2
Q. समकोण त्रिभुज का क्षेत्रफल कैसे ज्ञात करें?
समकोण त्रिभुज का क्षेत्रफल = (1/2) × b × h
Q. त्रिभुज में बगुला का सूत्र क्या होता है?
हीरोन का सूत्र
एक विषमकोण त्रिभुज का क्षेत्रफल = √s(s−a)(s−b)(s−c)
एस = (ए + बी + सी) / 2
जहाँ, a, b, और c = भुजाएँ
S = त्रिभुज का अर्ध-परिधि
Q. समद्विबाहु त्रिभुज के क्षेत्रफल की गणना कैसे करें?
एक समद्विबाहु त्रिभुज का क्षेत्रफल = 1/4 b√(4a2 – b2)
