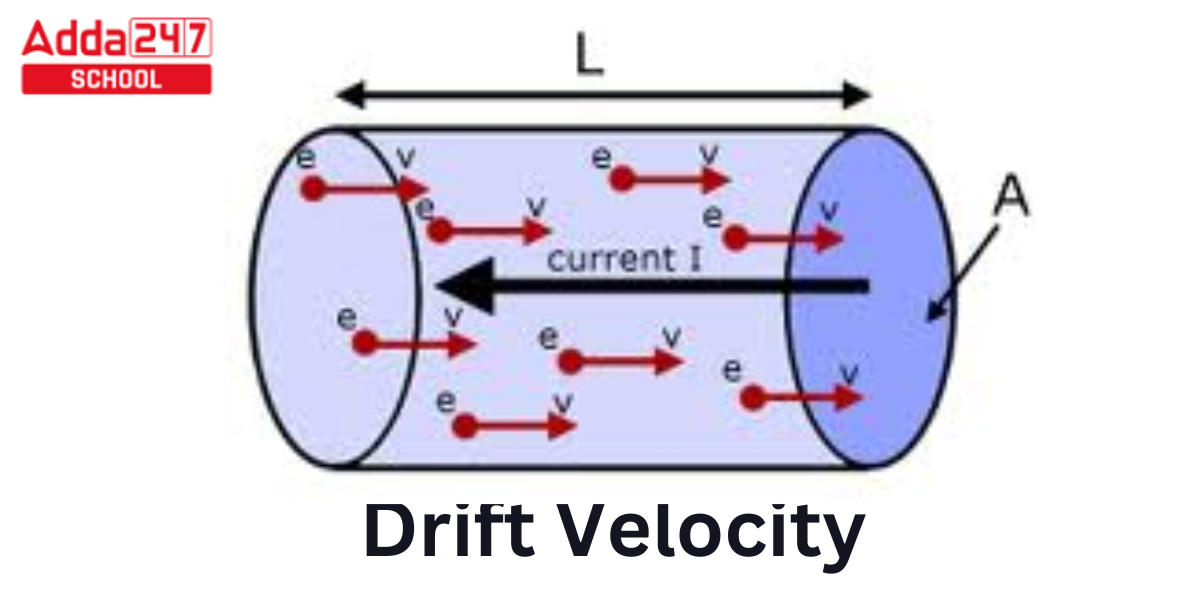
How do you calculate drift velocity?

The average speed at which electrons move away from the field is known as the "drift velocity." Beginning with the electrons' acceleration, a = F/m = eE/m. The drift velocity, or average velocity obtained as a result of this acceleration, is given by a*t = eEt/m.

What is drift velocity class 12?

The average speed obtained by charged particles (like electrons) in a material as a result of an electric field is known as drift velocity. M/s is the SI unit for drift velocity.

What is meant by drift velocity?

The average speed at which electrons "drift" in the presence of an electric field is known as drift velocity. The electric current is a result of the drift velocity (or drift speed).

What is the drift velocity of electrons?

the average speed that free electrons in a conductor travel at when an external electric field is placed across the conductor, causing the electrons to drift.

Drift Velocity Formula, Definition, SI Unit for Class 12 -

Table of Contents

Drift Velocity

Electrons and other subatomic particles constantly migrate in arbitrary ways. When exposed to an electric field, electrons do travel randomly, but they do so slowly in the direction of the applied electric field. The drift velocity refers to the overall speed of these electrons.

Define Drift Velocity

Drift velocity can be defined as:

The average velocity attained by charged particles, (eg. electrons) in a material due to an electric field.

Drift Velocity Definition

Drift velocity is a term commonly used in physics, particularly in the context of electrical conductivity in materials like metals. It refers to the average velocity of charged particles, such as electrons, as they move through a conductor in response to an applied electric field.

What is Drift Velocity?

Drift velocity refers to the average velocity of charged particles, such as electrons or ions, in a conductor or semiconductor material when an electric field is applied across it. It’s a concept commonly used in the study of electric currents and electrical conductivity.

When an electric field is applied to a conductor (like a wire), the electric field exerts a force on the charged particles within the conductor, causing them to move. However, individual charged particles don’t typically move very fast in response to the electric field. Instead, they experience frequent collisions with other particles, impurities, lattice vibrations, and defects within the material. These collisions impede the charged particles’ motion.

As a result, even though individual charged particles may have relatively high speeds between collisions, their net motion, on average, is quite slow. The drift velocity represents this slow, net average velocity of charged particles in response to the applied electric field.

Mathematically, drift velocity (v_d) can be expressed as:

$v_{d} =I/ n q A I$

Where:

$v_{d}$ is the drift velocity.
$I$ is the electric current in the conductor (the rate of flow of charge).
$n$ is the number density of charge carriers (e.g., electrons) in the material.
$q$ is the charge of a single charge carrier (e.g., the charge of an electron).
$A$ is the cross-sectional area of the conductor.

Drift velocity is generally much slower than the speed of individual charged particles. This is why electric current, which is defined as the flow of charge per unit time, can exist even though the charged particles themselves are not moving very fast.

Drift Velocity Formula for Class 12

The formula for drift velocity, often discussed in the context of electric current in class 12 physics, is given by:

$v_{d} =I/ n q A$

Where:

$m^{-3}$ ).
$1.6 \times 1 0^{- 19}$
$1.6 \times 1 0^{-19}$ coulombs, C).

This formula describes the average velocity of charge carriers in a conductor when an electric current is applied. The drift velocity is typically much smaller than the average velocity of electrons due to thermal motion. It represents the slow net movement of charge carriers in response to an applied electric field.

Drift Velocity Formula

The formula the calculate Drift Velocity is:

I = nAvQ

Here, I is the conductor’s current, measured in amperes; n is the number of electrons; A is the cross-sectional area of the conductor, measured in m2; v is the electrons’ drift velocity; and Q is the charge of an electron, measured in Coulombs.

Drift Velocity SI Unit

The SI unit of drift velocity is m/s. It is also measured in m²/(V.s).

Net Drift velocity of the electrons

Every substance that can conduct electricity and is warmer than absolute zero will have some free electrons travelling randomly. The electrons will naturally gravitate toward the positive potential when a potential is placed around a conductor, but as they go, they will hit atoms and either bounce back or lose some of their kinetic energy. The electrons will accelerate once more as a result of the electric field, and these random collisions will continue to take place. However, because the electric field causes the acceleration to always occur in the same direction, the electrons’ net velocity will also always be in that same direction.

CBSE Class 12 Physics Syllabus 2022-23 PDF Download

Relation between Drift Velocity and Electric Current

Mobility is always positive and relies on the type of charge carrier; an electron’s drift velocity is often measured in terms of 10-3 ms-1. Therefore, at this speed, it will take electrons approximately 17 minutes to go through a conductor that is 1 metre in length. However, amazingly, we can quickly turn on electrical appliances in our homes with the flick of a switch since an electric current is established at the speed of light and not with drift velocity.

Acceleration- Formula, Unit, Definition and Meaning

Define Relation between Drift Velocity and Current Density

The total amount of current flowing through a conductor with a certain cross-sectional area in a given amount of time is known as current density. We may calculate drift velocity using the following formula:

I = nAvQ
J = I/A = nVQ
Here, J is the current density measured in Amperes per square meter and v is the drift velocity of the electrons

As a result, we may state that the electrons’ current density and their drift velocity are directly proportional to one another. Additionally, as the strength of the electric field grows, the drift velocity and current flowing through the conductor do as well.

Formula of Drift Velocity in Other Words

The formula for Drift Velocity is given as follows:

v_d = -eEτ / m

Where,

v_dis the drift velocity ,

e is the charge of a electron,

E is the strenth of electric feild,

τ is the average relexatation time,

m is the mass of electron

Drift Velocity Derivation

As each free electron in the conductor experiences a force,

F = -eE

and the acceleration of each electron is

a = F / m

From both the above equations, we get

∴ a = -eE / m (where m is the mass of the electron)

At any instant of time, the velocity acquired by an electron having thermal velocity u₁ will be given using v = u + at as,

v₁ = u₁ + aτ₁

Where,

τ₁ is Time taken by Electron to collide with Positive Ion

v₁is Initial Velocity

Similarly, velocity acquired by electron, v₂ = u₂ + aτ₂ , v₂ = u₂ + aτ₂ , . . . . . . , v_n = u_n + aτ_n

The average velocity of all the free electrons in the conductor under the effect of the external electric field is the drift velocity v_d of the free electrons.

v_d= ( v₁ + v₂ + . . . . + v_n ) / n

⇒ v_d= ((u₁ + aτ₁) + (u₂ + aτ₂) + . . . . + (u_n + aτ_n)) / n

⇒ v_d= ((u₁ + u₂ + . . . +u_n)/n) + a((τ₁ + τ₂ + . . . . . + τ_n) /n) . . . (1)

when an Electric field is not applied to the conductor then there is no current in the conductor.

∴ (( u₁ + u₂ + . . . + u_n )/n) =0 . . . (2)

Putting equation 2 in equation 1, we get

v_d= 0 + aτ [where τ = ((τ₁ + τ₂ + . . . . . + τ_n) /n)]

where τ is the average relaxation time and it refers to the length each electron takes to recover from its most recent interaction with a conductor atom.

we know, a = -eE / m [from force experienced by charge in an electric field]

∴ v_d = -eEτ / m

where the negative sign shows the opposite direction of the electric field.

Drift Velocity, v_d = eEτ / m …(3)

Alternate Formula of Drift Velocity

If the length of the conductor and time taken by the electron to travel throughout the length of the conductor is given then drift velocity can be calculated using the following formula

$\bold{v_d = \frac{\Delta x }{\Delta t}}$

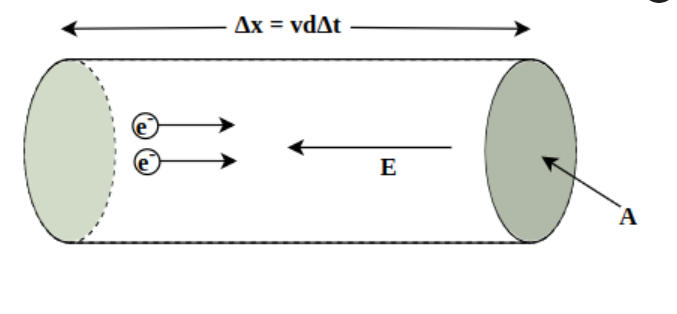
Due to the frequent collisions that electrons have, their drift velocity is small.
If the cross-section is constant, i ∝ J i.e. for a given cross-section area, the greater the current density, the larger will be current.
In the presence of an exceptionally large number of free electrons in a conductor, a tiny amount of drift velocity produces a large amount of electric current.
The electric bulb glows immediately when the switch is turned on because current transmission is practically as fast as light and involves electromagnetic processes.
In the presence of an electric field, the path of electrons between successive collision are curved and In the absence of an electric field, the path of electrons between successive collision is a straight line.
Free electron density in metal is