Acceleration
Acceleration is an important concept in physics and is used to define motion. Acceleration is defined as the rate of change in velocity which implies that an object is said to be accelerating when the velocity of the object is increasing or decreasing. Acceleration has both magnitude and direction which make it a vector quantity. The magnitude of the acceleration of an object is the combination of two factors net resulting force and the mass of the object, as per Newton’s Second Law of Motion. Let us understand in detail more about acceleration, its units, types, and graphs.
What is the Formula of Acceleration?
Acceleration is defined as the rate of change of velocity of an object concerning time. When the velocity of an object is changing, it is said to be accelerating.
Formula of Acceleration = Change in Velocity /Time taken
Acceleration can also be defined as the rate of change in velocity and the change over time. Acceleration can be positive, negative, or zero.
- Positive Acceleration occurs when the velocity of the object increases with time.
- Zero Acceleration occurs when the velocity is neither decreasing nor increasing it is zero.
- Negative Acceleration occurs when the velocity decreases with time. It is also known as retardation.
Acceleration Formula
The change in the velocity of an object in motion is defined as “v-u” where v is the final velocity and u is the initial velocity. Therefore, the acceleration of an object with initial velocity ‘u’ and final velocity ‘v’ and time took ‘t’ is
Acceleration = Change in Velocity /Time taken

Formula of Acceleration in Simple words
Acceleration is the rate of change of an object’s velocity with respect to time. In other words, acceleration describes how quickly an object’s speed or direction is changing over a specific period. The formula for acceleration can be expressed as follows:
Acceleration (a) = Change in Velocity (Δv) / Time Interval (Δt)
Where:
- Acceleration (a) is measured in units like meters per second squared (m/s²) in the International System of Units (SI).
- Change in Velocity (Δv) is the difference between the final velocity and the initial velocity of the object.
- Time Interval (Δt) is the duration over which the change in velocity occurs.
In simple terms, the formula tells us how much an object’s velocity changes per unit of time. If the acceleration is positive, it means the object is speeding up. If the acceleration is negative, it indicates the object is slowing down.
Acceleration Equation
The acceleration of an object is defined as the rate of change of its velocity with respect to time. Mathematically, it can be expressed using the following equation:
Where:
represents the acceleration.
(delta v) represents the change in velocity.
(delta t) represents the change in time.
Alternatively, you can also express acceleration in terms of the initial velocity (
), final velocity (
), and the time interval (
) as:
This equation tells you how quickly an object’s velocity changes over time, and it is typically measured in units such as meters per second squared (m/s²) in the International System of Units (SI).
Acceleration Unit
Acceleration is a vector quantity as it has both magnitude and direction. It is denoted by a. The unit of acceleration is meters per second squared which is m/s2. The dimensional formula of acceleration is [M0 L1 T-2].
Acceleration Formula Types
There are different types of Acceleration, namely uniform, non-uniform, average, and instantaneous, acceleration.
Uniform Acceleration Formula
When the velocity of an object changes in equal amounts during the same time intervals, then the object is said to be in uniform acceleration. During uniform acceleration, the direction and the magnitude do not change with time.
The formula for uniform acceleration relates the initial velocity (v₀), final velocity (v), acceleration (a), and displacement (s) of an object moving with constant acceleration. It’s commonly known as the second equation of motion. The formula is as follows:
v = v₀ + a * t
Where: v = final velocity of the object v₀ = initial velocity of the object a = acceleration of the object t = time taken for the object to reach the final velocity
This formula applies to an object moving in a straight line with uniform acceleration. Uniform acceleration means that the object’s acceleration remains constant during the time interval considered.
Using this formula, you can calculate the final velocity of an object when you know its initial velocity, acceleration, and the time it takes to achieve that final velocity.
It’s important to note that this formula only works for situations with constant acceleration. In real-world scenarios, acceleration may not always be constant, and more complex equations and calculus may be needed to describe the object’s motion accurately. However, for many introductory physics problems and situations involving constant acceleration (e.g., free-fall near the Earth’s surface), this formula is quite useful.
Example: motion of a car with constant velocity or a ball rolling down a slope.
Non-uniform Acceleration Formula
Non-uniform acceleration is also known as variable acceleration. In variable acceleration the velocity of the object changes by varying amounts during the same time interval. During non-uniform acceleration, the magnitude and direction both change with time.
The formula for non-uniform acceleration, where acceleration varies with time, is more complex than the formula for uniform acceleration. In such cases, you can use calculus and integrate the acceleration function with respect to time to determine the object’s velocity and position at any given time.
Let’s break down the formulas step by step for an object with non-uniform acceleration:
- Velocity (v) as a function of time (t): To find the velocity of an object at any given time, you need to integrate the acceleration function (a(t)) with respect to time (t). The formula for velocity as a function of time is:
v(t) = ∫ a(t) dt
Here, ∫ represents the integral symbol, and a(t) is the acceleration function with respect to time.
- Position (s) as a function of time (t): Similarly, to find the object’s position (displacement) at any given time, you need to integrate the velocity function (v(t)) with respect to time (t). The formula for position as a function of time is:
s(t) = ∫ v(t) dt
Where: v(t) = the velocity function as a function of time (obtained from the first step) s(t) = the position function as a function of time
To solve problems involving non-uniform acceleration, you need to know the function representing the acceleration as a function of time (a(t)). Once you have that function, you can perform the integrations to find the velocity function (v(t)) and then the position function (s(t)).
Example: A car changes its speed after every kilometer it travels.
Average Acceleration Formula
When the object changes its velocity for a particular specified time interval it is said to have average acceleration. The formula for calculating the average acceleration is given below.
Av =∆v/∆t or av = (vf-vi) / (tf -ti)
Here, vf is the final velocity
vi is the initial velocity
ti is the initial time
tf is the final time
Instantaneous Acceleration Formula
Instantaneous acceleration is defined as the ratio of change in velocity during a given time interval such that the time interval goes to zero. To calculate the instantaneous acceleration, the average velocity can be calculated between two points in time separated by ∆t and ∆t approaches zero. The result obtained is the derivation of the velocity function v(t) which is the instantaneous acceleration, which when mathematically written gives
a(t) = v(t)
Acceleration Velocity Time Graph
The curves indicate the velocity-time graph, where time is plotted along the x-axis, and velocity is plotted along the y-axis.
- When the velocity of an object is constant or Zero Acceleration.
- When the object is moving with a constant acceleration and the initial velocity is zero.
- When an object is moving with constant retardation
- When the object moves with non-uniform acceleration and the initial velocity is zero.
- When the acceleration is decreasing and increasing.
Difference between Acceleration and Velocity
| Criteria | Definition | Formula | Unit |
| Acceleration | Acceleration is defined as the change in the velocity of an object concerning time. | Velocity / Time | m.s-2 |
| Velocity | Velocity is defined as the speed of an object in a particular direction. | Displacement/Time | m.s-1 |
Acceleration Formula Class 9 and 11 Examples
1.If a car accelerates from 5 m/s to 10 m/s in the 20s. Calculate its acceleration.
Ans. Given,
Initial Velocity, u = 5 m/s
Final Velocity, v = 10 m/s
Time Taken, t = 20 s
Acceleration, a= (v-u)/t
= (10m/s – 5m/s) / 20
= 0.25 m/s2
- If a truck is going at a speed of 100 km/h is slowed down and brought to 70 km/h in 5s. Calculate the retardation of the truck?
Ans. Given,
Initial Velocity, u = 90 m/s or 90 x = 25 m/s
Final Velocity, v = 72 m/s or 72 x = 20 m/s
Time Taken, t = 20 s
Acceleration, a= (v-u)/t
= (20m/s – 25m/s) / 20
= -0.25 m/s2
- If a car is moving from rest and then accelerates uniformly at 8.2 m/s2 for 10s. Find the velocity of the train in 10s.
Given,
Initial Velocity, u = 0 m/s (car is in rest)
Time Taken, t = 10 s
Acceleration, a= 8.2 m/s2
v = u + at
= 0 + 8.2 x 10
= 82 m/s
Formula for Acceleration QNAs
- What is the average acceleration over time?
Ans. The average acceleration over time ka is defined as the total change in velocity in given intervals of time divided by the total time taken for the change.
- What is Acceleration due to gravity?
Ans. The acceleration due to gravity is defined as the acceleration experienced by the earth’s gravitational pull.
- What do you understand by Centripetal Acceleration?
Ans. Centripetal Acceleration is defined as the acceleration points toward the center of the curvature since the velocity is continuously changing and acceleration is present.
- How acceleration is related to force?
Ans. Acceleration is directly proportional to the force applied to an object with constant mass.
- Why acceleration is a vector quantity?
Ans. Acceleration is a vector quantity because it is related to both magnitude and direction.

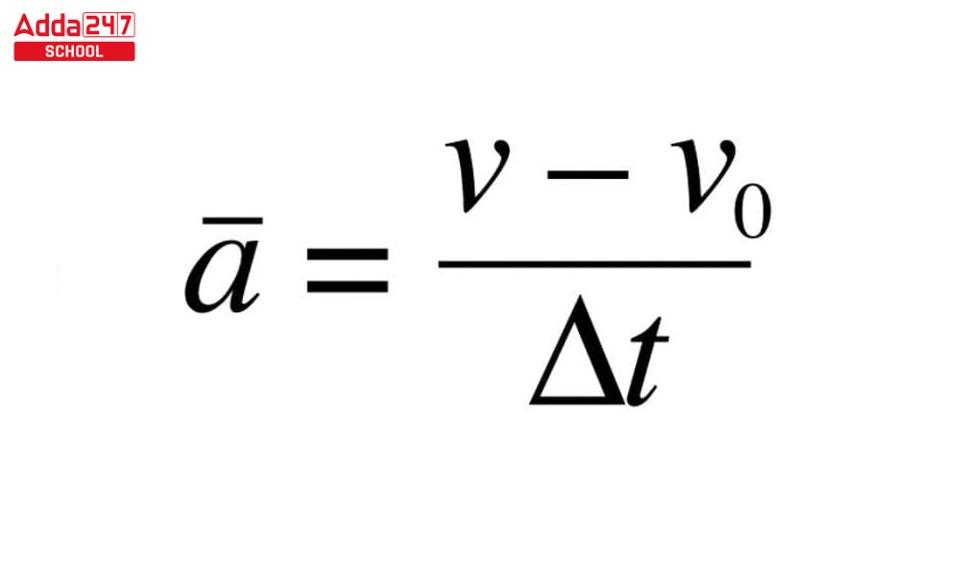







 Try CUET College Predictor 2025 to Predi...
Try CUET College Predictor 2025 to Predi...
 CUET Result 2025 OUT (Today) @cuet.nta.n...
CUET Result 2025 OUT (Today) @cuet.nta.n...
 Why the Delay in CUET UG 2025 Results? C...
Why the Delay in CUET UG 2025 Results? C...









