Table of Contents
वर्ग, घन, वर्गमूळ आणि घनमूळ
प्रिय वाचकांनो, गणिताच्या आकर्षक क्षेत्रामध्ये मनमोहक प्रवासात आपले स्वागत आहे! या ब्लॉगमध्ये, आम्ही चार मूलभूत गणितीय क्रियांचा शोध घेत आहोत ज्यांनी शतकानुशतके मनाला कुचकामी आणि गोंधळात टाकले आहे: वर्ग, घन, वर्गमूळ आणि घनमूळ. आगामी स्पर्धा परीक्षा जसे की, आदिवासी विकास विभाग भरती 2023 साठी हा एक महत्वाचा टॉपिक आहे. चला मग या लेखात आपण अंकगणित विषयातील वर्ग, घन, वर्गमूळ आणि घनमूळ बद्दल संपूर्ण माहिती घेऊयात. या लेखात आम्ही 1-30 वर्ग संख्या, 1-30 वर्गमूळ संख्या, 1-30 घन संख्या आणि 1-30 घनमूळ संख्या दिल्या आहेत.
वर्ग, घन, वर्गमूळ आणि घनमूळ: विहंगावलोकन
गणितात, x संख्येचे वर्गमूळ ही संख्या y असते जी y² = x असते. दुसर्या शब्दांत, संख्येचे वर्गमूळ मूळ संख्येच्या बरोबरीच्या संख्येच्या पटीत असते. उदाहरणार्थ, 4 आणि −4 हे 16 चे वर्गमूळ आहेत कारण 4² = 16 आणि (-4)² = 16. गणितात, संख्येचा घन हा त्या संख्येचा तीन वेळा गुणाकार केल्याने होतो. उदाहरणार्थ, 2 चा घन 2 × 2 × 2 = 8 आहे. संख्येच्या घनाला संख्येची घन घात असेही म्हणतात. खालील तक्त्यात वर्ग, घन, वर्गमुळ आणि घनमुळ बद्दल विहंगावलोकन पहा.
| वर्ग, घन, वर्गमूळ आणि घनमूळ: विहंगावलोकन | |
| श्रेणी | अभ्यास साहित्य |
| उपयोगिता | आदिवासी विकास विभाग भरती 2023 व सर्व स्पर्धा परीक्षांसाठी |
| विषय | अंकगणित |
| टॉपिकचे नाव | वर्ग, घन, वर्गमूळ आणि घनमूळ |
| लेखातील प्रमुख मुद्दे |
|
वर्ग: 1 ते 30 संख्येचा वर्ग (1-30 Squares)
जेव्हा आपण पूर्णांक संख्येला स्वतःनेच गुणाकार करतो तेव्हा आपल्याला मिळणारे मूल्य हे त्या पूर्णांकाचा वर्ग असतो. उदाहरणार्थ, 8 पूर्णांक आहे. 8 × 8 = 64, 8 चा वर्ग आहे.
जर ‘x’ ही संख्या असेल, तर त्याचा वर्ग ‘x²’ ने दर्शविला जाईल.
| 1 ते 30 चे वर्ग संख्या (1-30 Squares): (x²) = 1 to 30 | ||
| 1² = 1 | 11² =121 | 21² =441 |
| 2² = 4 | 12² =144 | 22² =484 |
| 3² =9 | 13² =169 | 23² =529 |
| 4²= 16 | 14² =196 | 24² =576 |
| 5² =25 | 15² =225 | 25² =625 |
| 6² =36 | 16² =256 | 26² =676 |
| 7² =49 | 17² =289 | 27² = 729 |
| 8² =64 | 18² =324 | 28² = 784 |
| 9² =81 | 19² =361 | 29² = 841 |
| 10² =100 | 20² =400 | 30²= 900 |
वर्गमूळ: 1 ते 30 संख्येचे वर्गमूळ (1-30 Square Roots)
| 1 ते 30 संख्येचे वर्गमूळ (1-30 Square Root): √x = 1 to 30 | ||
| √1 = 1 | √11 = 3.317 | √21 = 4.583 |
| √2 = 1.414 | √12 = 3.464 | √22 = 4.690 |
| √4 = 2 | √13 = 3.606 | √23 = 4.796 |
| √3 = 1.732 | √14 = 3.742 | √24 = 4.899 |
| √5 = 2.236 | √15 = 3.873 | √25 = 5 |
| √6 = 2.449 | √16 = 4 | √26 = 5.099 |
| √7 = 2.646 | √17 = 4.123 | √27 = 5.196 |
| √8 = 2.828 | √18 = 4.243 | √28 = 5.292 |
| √9 = 3 | √19 = 4.359 | √29 = 5.385 |
| √10 = 3.162 | √20 = 4.472 | √30 = 5.477 |
घन: 1 ते 30 संख्येचा घन (1-30 Cubes)
जेव्हा आपण पूर्णांकाचा तीन वेळा गुणाकार करतो तेव्हा आपल्याला मिळणारे मूल्य हे त्या पूर्णांकाचे घन असते.
उदाहरणार्थ, 7 हा पूर्णांक आहे. 7 चा घन = 7×7×7 = 343 आहे.
जर ‘×’ पूर्णांक असेल, तर त्याचा घन ‘x³’ ने दर्शविला जातो.
| 1 ते 30 चे घन संख्या (1-30 Cubes): (x³) = 1 to 30 | ||
| 1³ = 1 | 11³ = 1331 | 21³ = 9261 |
| 2³ = 8 | 12³ = 1728 | 22³ = 10648 |
| 3³ = 27 | 13³ = 2197 | 23³ = 12167 |
| 4³ = 64 | 14³ = 2744 | 24³ = 13284 |
| 5³ = 125 | 15³ = 3375 | 25³ = 15625 |
| 6³ = 216 | 16³ = 4096 | 26³ = 17576 |
| 7³ = 343 | 17³ = 4913 | 27³ = 19683 |
| 8³ = 512 | 18³ = 5832 | 28³ = 21952 |
| 9³ = 729 | 19³ = 6859 | 29³ = 24389 |
| 10³ = 1000 | 20³ = 8000 | 30³ = 27000 |
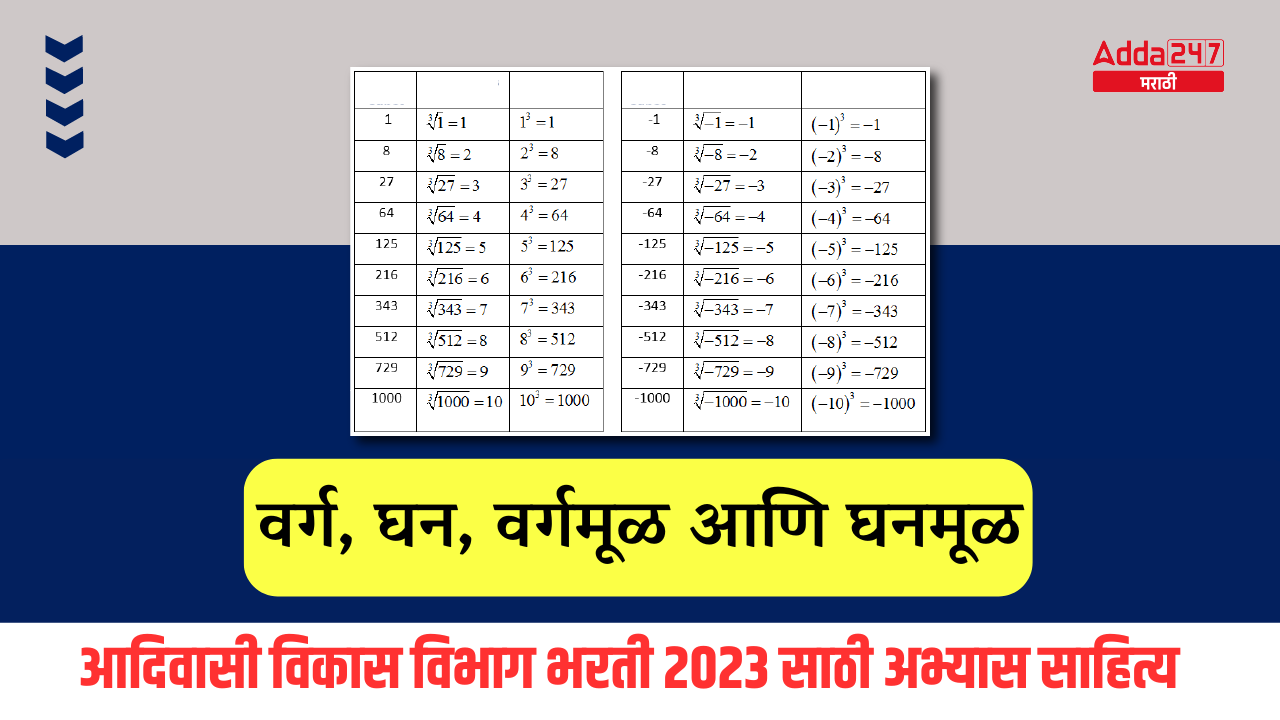
घनमूळ : 1 ते 30 संख्येचे घनमूळ (1-30 Cube Roots)
| घनमूळ : 1 ते 30 संख्येचे घनमूळ (1-30 Cube Roots) | ||
| ∛1 = 1 | ∛11 = 2.224 | ∛21 = 2.759 |
| ∛2 = 1.26 | ∛12 = 2.289 | ∛22 = 2.802 |
| ∛3 = 1.442 | ∛13 = 2.351 | ∛23 = 2.844 |
| ∛4 = 1.587 | ∛14 = 2.41 | ∛24 = 2.884 |
| ∛5 = 1.71 | ∛15 = 2.466 | ∛25 = 2.924 |
| ∛6 = 1.817 | ∛16 = 2.52 | ∛26 = 2.962 |
| ∛7 = 1.913 | ∛17 = 2.571 | ∛27 = 3 |
| ∛8 = 2 | ∛18 = 2.621 | ∛28 = 3.037 |
| ∛9 = 2.08 | ∛19 = 2.668 | ∛29 = 3.072 |
| ∛10 = 2.154 | ∛20 = 2.714 | ∛30 = 3.107 |
महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळावा.