Rectilinear Motion of a Particle – Definition, Types, Formulas, Examples

Rectilinear Motion of a Particle: Rectilinear motion is one of the core concepts in the world of dynamics. Every object in the world undergoes motion. Travelling from one place to another is an example of motion. In layman’s words, going from one place to another is known as motion. So, first diving into the world of rectilinear motion, let us first recall the concept of motion in scientific terms.

What is Motion?

A body is said to be in motion if its position varies with respect to space, time, and its surroundings. One of the most prevalent things we experience on a daily basis is motion. A moving car, a child jogging down the street, or a fly flying through the air are all examples of motion. Different motions, such as projectile motion, rectilinear motion, rotational motion, etc., can be produced by a particle depending on the path it follows. In this article, we will explore different aspects of the rectilinear motion.

Rectilinear Motion of a Particle

Definition of Rectilinear Motion

A particle is said to exhibit a rectilinear motion if it travels along a straight line or a straight path. So, the motion which is restricted to a single direction or line is known to be a rectilinear motion. So, we can define the rectilinear motion using only one co-ordinates. That is, rectilinear motion of a particle means the motion in which a particle travels along any one of the axis. We can define the motion of any object using velocity, displacement and acceleration. In rectilinear motion, all these parameters have only one dimension and the same path. Thai is why, this motion is also known as linear motion or motion in a straight line.

Examples of Rectilinear Motion of a Particle

As discussed above, in rectilinear motion, the particle travels along any one direction. Some of the examples of rectilinear motion of a particle are given below:

• A vehicle travelling on a straight road
• Ball rolling down an inclined ramp
• An object in free fall
• Fall of a fruit from the tree
• Marching of soldiers
• Motion of an arrow hitting the target
• Motion of a bullet fired from a gun
• Motion of an elevator

The straight-line nature of a rectilinear motion will be more clear to you by observing the diagram given below.

As we can observe from the above diagram, a particle in rectilinear motion travels along a straight line while a particle in non-rectilinear motion follows a non-straight path.

Rectilinear Motion of a Particle Formula

The rectilinear motion of a particle can be expressed mathematically. These equations also show the one-dimensional nature of this motion. Let us derive its formula for different motion-related parameters.

Assume an object initially at point X1. After time t, the object is now located at point X2.

Displacement

so, Displacement = Change in position of the particle = X2 – X1 = X

so, we can observe the distance travelled formula needs only one co-ordinate.

Velocity and Acceleration

Velocity is defined as the rate of change of displacement with time or the ratio between displacement and time. Mathematically, velocity is defined as:

V = d(X)/dt = X/t

where, V = velocity

t = time period

Acceleration is defined as the rate of change of velocity. It is denoted as “a”. Mathematically, acceleration is given by:

a = dv/dt = d²(X)/dt

Types of Rectilinear Motion of a Particle

Rectilinear motion of a particle can be categorized in three types based on the motion-related parameters. These three types of rectilinear motion are given below:

1. Uniform Rectilinear Motion: The uniform rectilinear motion of a particle means the particle travels at a constant speed with 0 acceleration. That is, the object travels equal distance in equal time interval.
2. Uniformly accelerated Rectilinear Motion: In this motion, the object travels with a constant acceleration. The velocity of object changes at a constant rate.
3. Non-uniformly accelerated Rectilinear Motion: In this type of rectilinear motion, the object travels at irregular acceleration. There is no co-relation between displacement, velocity and time.

Rectilinear Motion of a Particle Graph

The rectilinear motion of a particle can be represented graphically. The graphical representation helps to understand the nature of this motion. The graph can be plotted for distance-time, velocity-time, or acceleration-time. The nature of the graph will depend on the parameters for which it is plotted and the type of rectilinear motion. The distance-time graph of a uniform rectilinear motion of a particle is shown below.

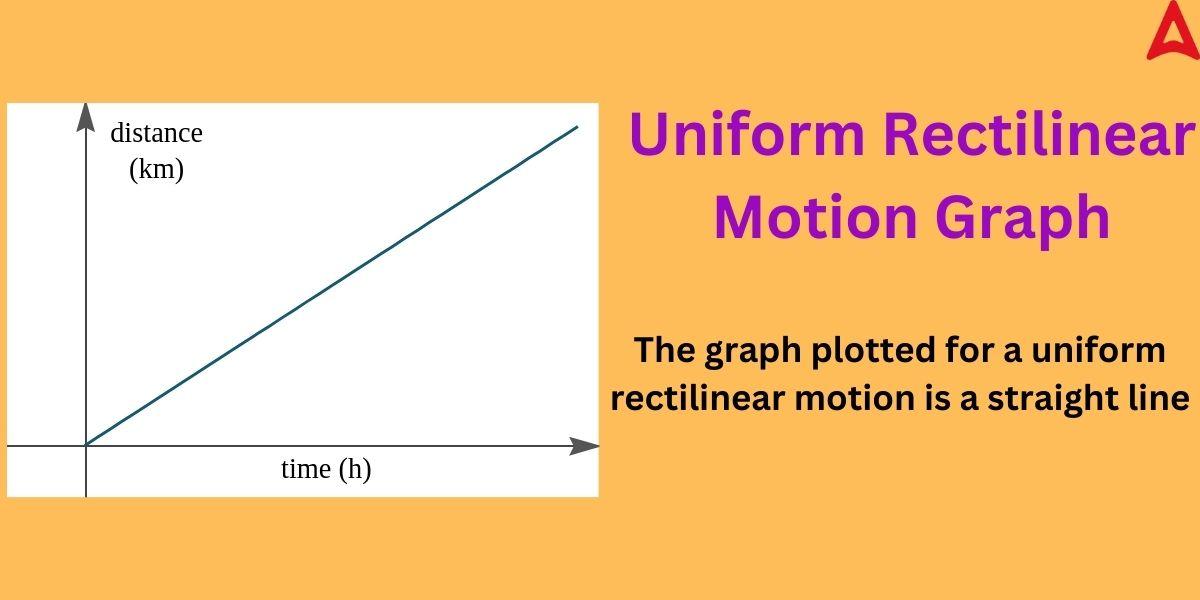
As we can observe from the above diagram, the distance is taken as y-axis and time is taken as x-axis. The graph is a straight line showing that the particle covers equal distance in equal time. The tangent of this graph will give the value of the velocity of the particle.

Rectilinear Motion of a Particle Derivation

We can derive the formulas for the uniformly accelerated rectilinear motion of a particle. Let us derive the formulas for the same.

Let us consider a particle which is at position Po at time t =0

the initial velocity of the particle = u

let there be no acceleration initially

so, dv/dt = 0

in the absence of acceleration initial velocity = constant = u

that is, dx/dt = u

or, dx = u dt —(i)

let the particle travels from Po to P1 in time t= 0 to t

so integrating the equation (i) taking the above-mentioned lower and upper limits

∫dx = ∫u dt

∫dx = u ∫ dt

P1 – Po = u (t-0)

or, P1 = Po + u.t

It is the distance formula for a particle in rectilinear motion.

The formula for uniformly accelerated motion can be derived too.

Let the uniform acceleration applied on the object be a

Hence, dv/dt = a

or dv = adt

As the velocity at time t = 0 is taken as u. let at time = t, the velocity becomes v

So, integrating both sides with lower and upper limits of dv = u and v respectively while the lower and upper limits of dt= 0 and t respectively.

∫ dv = ∫ a dt

∫ dv = a ∫ dt

v-u = a (t-0)

v = u + at ——(ii)

as v = dx/dt

so putting this in equation (ii), we get

dx/dt = u + at

dx = (u + at) dt

Taking integration on both sides

∫ dx = ∫ (u + at) dt

∫ dx = ∫ u dt + ∫ dt

Taking the respective lower and upper limits for each parameter, we get

P1 – Po = u.t + (1/2) a.t²

or, P1 = Po + u.t + (1/2) a.t² ———-(iii)

we can derive the following formula in terms of displacement too.

as acceleration (a) = (v – u)/t

or, t = (v – u)/a

putting the above value of t in equation (iii), we get,

P1 = Po + u(v – u)/a + (1/2) a. (v – u)²

on solving the above equation, we get

v² = u² – 2.a(P1 – Po)

Rectilinear Motion of a Particle Class 9 and Class 11

The rectilinear motion of a particle is an important concept in class 9 and class 11. Students must go through this article to have a clear understanding of this topic. The important formulas related to this topic for both classes is listed below.

• distance = speed x time
• displacement = velocity x time
• v = u + at
• D = u.t + (1/2)a.t²
• v² – u² = 2.a.D

Rectilinear Motion of a Particle Examples

Some of the solved examples on rectilinear motion concept given below. These solved questions will help students prepare this topic in a better way.

Example 1: If the velocity of a particle is given to be 50 m/s. What will be the position of a particle after 10 s if the particle is currently at 20 m on the +x-axis.

Solution: Given velocity (v) = 50 m/s

time (t) = 10 s

initial position = 20 m

as no acceleration is present, so velocity will be constant.

Using the formula for the uniform rectilinear motion

P1 = Po + u.t

P1 = 20 + 50 x 10

P1 = 520 m

Hence, the particle will be at 520 meter

Example 2: What position will a car occupy after 10 seconds of acceleration at 10 m/s? The car is currently at rest.

Solution: Given, initial velocity (u) = 0

time (t) = 10

acceleration (a) = 10

using the formula D = u.t + (1/2) a.t²

D = 0 x 10 + (1/2) x 10 x 10

D = 50 meter

So, the car will be 50 meter ahead of the current position.

Example 3: What will be distance covered by an object if its speed is 18 km/hour and the time given is 20 s.

Solution: given, speed = 18 km/hour

time = 20 s

as the speed is in km/hour, so first we will convert it into m/s

18 km/hour = 18 x (5/18) m/s = 5m/s

as, distance = speed x time

so, distance = 5 x 20

Hence, the distance covered by the object = 100 meter

Sharing is caring!