Doppler Effect- Explanation, Formula, Applications, Examples

The Doppler Effect is one of the most intriguing concepts in physics which explains many real-world phenomena. It is connected to waves and hence it can be associated with both light and sound waves. This is an important property of the sound waves and light waves. It is sometimes also known as the Doppler shift, especially in the case of light waves. It basically illustrates the effect of the motion of the observer, source or both on the characteristics of waves. Let us explore this concept in a thorough way by going through its formula, applications, and examples for both light waves and sound waves.

Doppler Effect

Doppler effect is an important phenomenon which can be easily observed in the real-world scenario. It also holds a great importance in the field of planetary motion. It is an observed phenomenon which does not alter the real nature of the waves. You all must have experienced this phenomenon. For example, when a train approaches the platform, the sound of its horn keep increasing while it keeps fading away while leaving the railway station. It is related to the concentration of waves reaching a particular observer. The object emitting the waves is known as the source while the person/object receiving the waves is known as observer. After knowing the basic terms, let us now take a deep dive into its technical explanation.

Doppler Effect Explanation

The Doppler Effect is a phenomenon that describes the change in frequency or wavelength of a wave in proportion to an observer moving relative to the source of the wave. It is named after the Austrian physicist Christian Doppler who first postulated it in 1842. When a wave source or an observer moves, it causes a change in the wave’s frequency relative to the observer. This is a result of how close or far the source and observer are to one another. This effect is observed in both sound and light waves. A source’s waves are compressed as they move in the direction of the observer. In contrast, waves from a source that is moving away from the observer become longer. Let us understand this concept by taking an example.

Doppler Effect Example

The Doppler Effect can be understood in a crystal clear manner through the diagram given below.

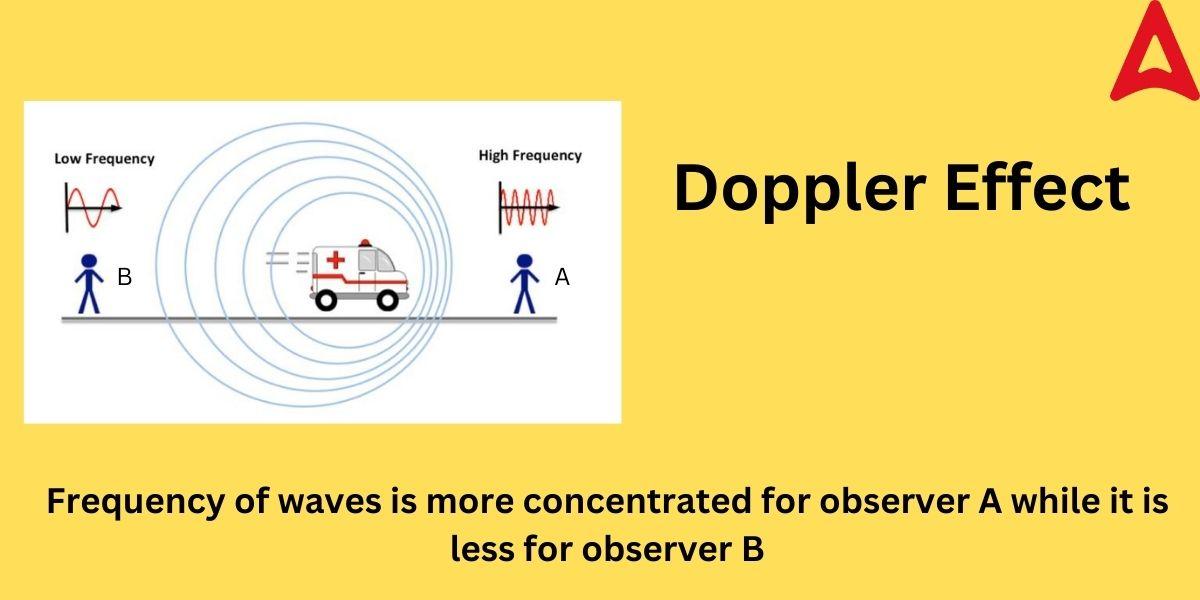
In the above figure we have two observers A and B. An ambulance is approaching the observer A and leaving/going far away from the observer B.

As we can clearly observe from the above diagram, the concentration of waves is more at the observer A side whereas the concentration of waves at the observer B is less. This results in the lesser frequency of sound for observer B and higher frequency of sound for the observer A. So, the observer A will receive a higher magnitude of sound leading to more loudness as compared to the observer B.

Doppler Effect Formula

The variation in frequency of the received waves due to the relative motion of the observer and source can be mathematically expressed using the Doppler Effect formula.

The Doppler Effect Formula is given by:

fo = f x ((V ± Vo)/(V ± Vs))

where, fo = observed frequency by the observer

V = velocity of the waves

Vs = velocity of the source

Vo = velocity of the observer

f = original frequency emitted by the source

The velocity of the surrounding medium (like air) also affects the observed frequency of sound waves. It is important to note that the above formula is used for sound waves. The above formula can be modified as per the requirement in different case. For example, in some cases the observer might be at rest or the source might be at rest. The Doppler Effect formula for different cases is shown below.

Doppler Effect Formula in Different Scenarios

As stated above, there can arise different situation depending on the velocity of the object and the observer. The modified Doppler formula for different cases is given below.

Case I: Observer Moving Towards the Source at Rest

as the source is at rest, so, Vs = 0

and the observer is approaching the source, so we will use + sign with Vo

The modified formula hence becomes:

fo = f x ((V + Vo)/V)

Case II: Source Moving Towards the Observer at Rest

as the observer is at rest, so, Vo = 0

and the source is approaching the observer, so we will use – sign with Vs to make fo bigger overall

The modified formula hence becomes:

fo = f x (V/(V-Vs))

Case III: Observer Moving Away from the Source at Rest

as the source is at rest, so, Vs = 0

and the observer is moving away from the source, so we will use – sign with Vo

The modified formula becomes:

fo = f x ((V – Vo)/V)

Case IV: Source Moving Away from the Observer at Rest

as the observer is at rest, so, Vo = 0

and the source is moving away from the observer, so we will use + sign with Vs to make fo smaller overall

The modified formula hence becomes:

fo = f x (V/(V+Vs))

Case V: Source and Observer both Moving Towards Each Other

In this case, the modified Doppler Effect formula is given by:

fo = f x ((V + Vo)/(V – Vs))

Case VI: Source and Observer both Moving Away from Each Other

In this case, the modified Doppler Effect formula is given by:

fo = f x ((V – Vo)/(V + Vs))

Doppler Effect in Light

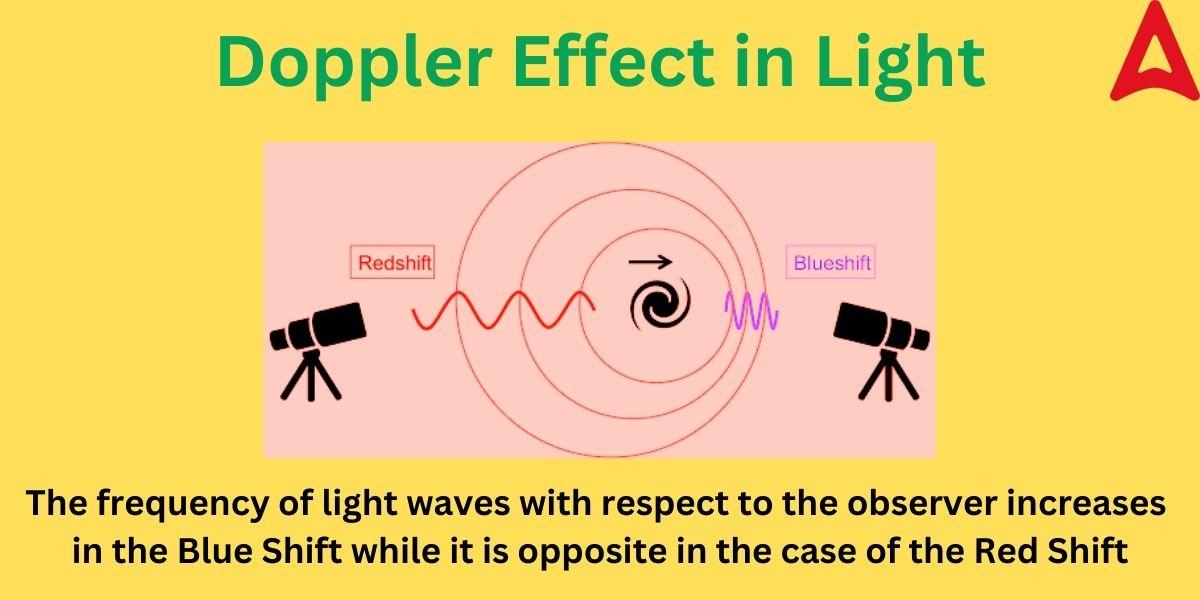
As mentioned earlier, the Doppler effect is observed in the light waves too. It is more widely pronounced as Doppler shift in the case of lights. The apparent shift in the frequency of the light that the observer perceives as a result of relative motion between the source of the light and the observer is known as the Doppler effect of light. It is responsible for the red shift and blue shift phenomenon of the light. This effect is used in explaining various aspects of planetary motion and astronomy. Unlike sound waves, light waves do not require any medium to travel. So, the velocity of the surrounding medium does not effect the frequency/wavelength nature of the light waves for the observer. The doppler effect in light depends only on the relative motion of the observer and the source. After getting a basic idea, let us now understand the phenomena of red shift and blue shift occurring due to this effect.

Red Shift: The frequency that the observer receives will be lower than the frequency that the light source transmits as it moves away from the observer. The visible light spectrum shifts towards the red end as a result. It’s known as the redshift in astronomy.

Blue Shift: The frequency perceived by the observer will be higher than the frequency broadcast by the source when the light source advances in that direction. The visible light spectrum shifts in favor of the high-frequency region as a result. It is referred to as the blue shift.

Application of Doppler Effect

There are many practical uses of the Doppler Effect. Its applications can be found in different fields in our daily life. Some of the areas in which this effect finds its application are listed below

• Astronomy
• Satellite Communication
• GPS Navigation
• Radars
• Remote Sensing
• Sonic Boom Analysis
• Developmental Biology

Doppler Effect Solved Examples

We have provided students with some solved examples on the Doppler Effect topic. By practicing these solved questions on the doppler effect formula, students will have a better understanding of this concept.

Example 1: The siren of an ambulance is blaring as it approaches you. The frequency of the siren is 440 Hz. The ambulance is travelling at a 30 m/s speed. What frequency do you hear the siren at rest? The velocity of sound waves is given to be 360 m/s in the air.

Solution: As we have been given

Velocity of the sound waves (V) = 360 m/s

Velocity of the source (Vs) = 30 m/s

actual frequency of the source (f) = 440 Hz

Velocity of the object (Vo) = 0

By using the Doppler Effect formula for the source approaching the observer at rest:

fo = f x (V/(V-Vs))

fo = 440 x (360/(360-30))

fo = 440 x (360/330)

fo = 440 x (36/33)

fo = 480 Hz

Example 2: What will be the actual frequency of the source at rest when the observed frequency is 600 Hz. The observer is moving away from the source with a velocity of 50 m/s. Take the speed of the sound waves in air to be 350 m/s.

Solution: Given,

Vs = 0

Vo = 50 m/s

fo = 600 Hz

V = 350 m/s

By using the Doppler Effect formula for the Observer Moving Away from the Source at Rest

fo = f x ((V – Vo)/V)

600 = f x ((350-50)/350)

600 = f x (300/350)

600 = f x (6/7)

f = 600 x (7/6)

f = 700 Hz

Therefore, the actual frequency of the source = 700 Hz

Example 3: X and Y buses are travelling with a speed of 432 km/h in the direction of one another. What is the apparent frequency of the horn heard by the passenger in bus X if the horn frequency generated by bus X is 800 Hz? (Sound travels through air at a speed of 360 m/s).

Solution: We have been given two buses X and Y. As the horn is generated by bus X, so, it is the source and the passenger in bus B will be the observer.

We have been given Vo = Vs = 432 km/h

on converting the velocity of the source and observer in meter per second we get:

432 x (5/18) = 120 m/s

V = 360 m/s

actual frequency (f) = 800 Hz

Using the doppler effect formula for the scenario Source and Observer both Moving Towards Each Other

fo = f x ((V + Vo)/(V – Vs))

fo = 800 x ((360 + 120)/(360-120)

fo = 800 x (480/240)

fo = 800 x 2

fo = 1600 Hz

Sharing is caring!