Elastic Potential Energy: Definition, Formula, Derivation, Examples

Elastic Potential Energy: A fundamental idea in physics called elastic potential energy can explain how energy is stored and released in elastic materials like springs and rubber bands. The energy of any form is basically the potential to do work. Before delving into the world of this special energy, let us first recall the concept of potential energy. Potential energy is the energy possessed by a particle due to its special position, orientation, or shape. It is one of the most important concepts related to energy. Due to its usefulness, it finds its applications in many branches of science and engineering. Let us understand this concept in a detailed manner.

Elastic Potential Energy

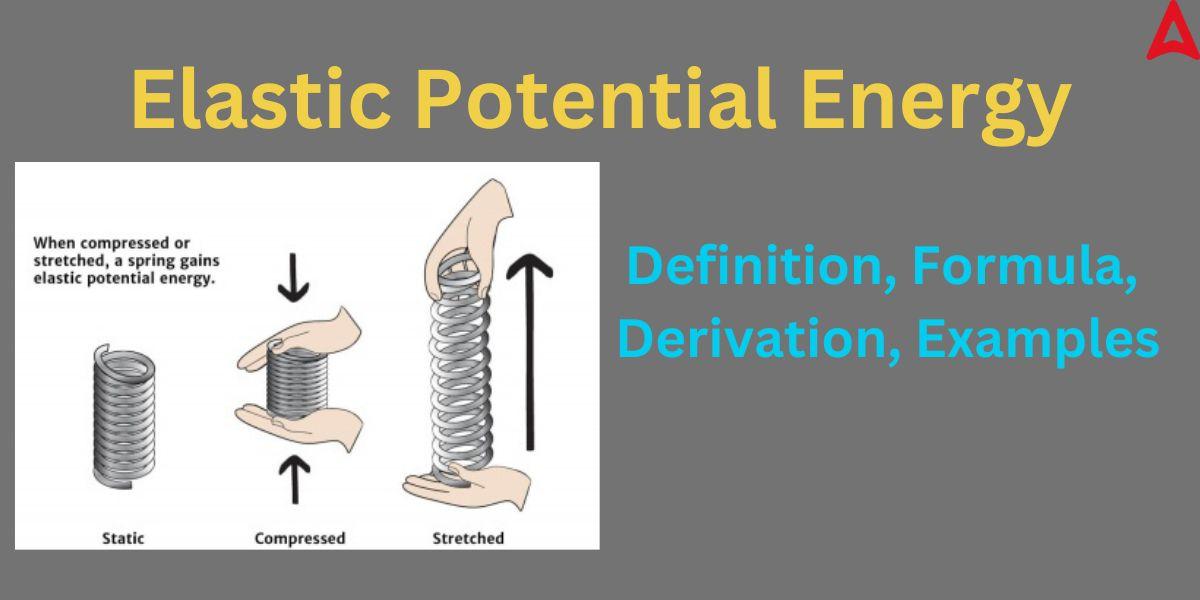
After getting the basic understanding of the energy and potential energy, w can now understand this concept clearly. Elastic potential energy is a special form of energy associated with elastic objects. As we know, elastic bodies have the ability to retain its original shape. whenever we apply a force on these elastic objects, its shape changes due to work done by the applied force. This is stored in an equivalent amount in the form of energy that help elastic particles to regain its shape. This equivalent amount of force is known as the Elastic potential energy. For example, the potential energy of an elastic object is increased when an elastic object, like a spring, is stretched or compressed. It is possible to convert this potential energy into kinetic energy or use it in a variety of ways.

Elastic Potential Energy Definition

The potential energy that is stored when an elastic item is stretched or compressed by an external force, such as the stretching of a spring, is known as elastic potential energy. It is equivalent to the work required to stretch the spring, which is dependent on both the length of the stretch and the spring constant k. In other words, it is energy that is stored when a force is used to deform an elastic object. Until the force is released and the object springs back to its original shape, doing work in the process, the energy is retained. The object may be compressed, stretched, or twisted during the deformation. It is also known as the spring potential energy in case of a spring.

Elastic Potential Energy Examples

There are many real-life examples of this potential energy. Some of the elastic potential energy examples are listed below.

• Elongation or compression of spring
• A stretched bow
• Twisted rubber band
• Stretched slingshot
• A bouncy ball when squeezed as it bounces off a brick wall
• A bent diving board before the diver jumps

As you can observe from the above examples that in each scenario, the energy is stored due to the compression, stretching, or torsion.

Elastic Potential Energy Formula

The value of this energy stored in an elastic object can be derived using mathematical concepts. The formula for the same is given below.

The potential energy stored in an elastic object is given by:

U = (1/2) k.x²

where, U = Elastic potential energy

k = spring constant

x = distance by which the object is displaced from its original shape/position

Elastic Potential Energy Units

The potential energy stored in an elastic object is denoted by U. Its SI unit is same as that of all other forms of energy, i.e., Joule (J). Its SI unit can also be expressed as Kg-m²/s². We can find out the dimensional formula for his special energy. The dimensional unit of the potential energy stored in an elastic object is given by:

[M¹L²T^-2]

Elastic Potential Energy Derivation

As we observed above, the potential energy stored in an object is given by the formula (1/2) k.x². We can derive this equation by using mathematical concepts. The derivation of this formula is based on the energy-work duality. Let us derive this expression through the diagram given below.

As you can observe in the above diagram that a spring is displaced by a distance of x by a force F. The energy is stored in the spring in the form of potential energy in the opposite direction of the displacement. Suppose initially the spring is at rest (x =0).

Let a force F be applied on the spring that displaces it by a small distance dx

Then the small amount work done (dw) by the force on the spring will be given by:

dw = F. dx —————-(1)

By Hooke’s law, F = -k . x

where k is the spring constant and x is the displacement.

Putting these values of F in equation (1)

dw = -k. x. dx

the negative (-) shows the opposite direction in which the force is restored

To find the total work done (W) in changing the spring from x = 0 to x = x, we will integrate the above equation

∫ dw = ∫ – k. x. dx

ignoring the negative sign

∫ dw =  k ∫ x. dx

W – 0 = k[(x²/2) – 0²/2]

W = (1/2)k.x²

as work done is stored in the form of elastic potential energy

Hence, U = (1/2)k.x²

This derivation is also known as the derivation of potential energy in a stretched spring. It is one of the most important derivation in class 11 physics.

Elastic Potential Energy Example Problems

Some of the solved example problems on this topic is given below. These solved questions will help students in preparing this topic in a better way.

Example 1: A spring that has a 100 N/m spring constant is elongated by 0.4 meters. Determine how much elastic potential energy is contained in the spring.

Solution: given, spring constant (k) = 100 N/m

displacement (x) = 0.4 m

using the formula U = (1/2)k.x², where U = potential energy associated with elastic objects

U = (1/2) x 100 x (0.4)²

U = 8 joules

Example 2: A compressed spring has a 400 N/m spring constant and a potential energy of 50 joules. Determine the spring’s displacement as a result of the potential energy.

Solution: given, potential energy of a spring (U) = 50 joules

spring constant (k) = 400 N/m

As U = (1/2) k. x²

50 = (1/2) 400. x²

x² = 50/200

x² = 1/4

x = 1/2

Hence, the spring will be displaced by 0.5 meter

Example 3: When the load of 5 kg is connected to the vertical spring, it is elongated by 10m. Find out the potential energy stored in the spring. Take g = 10ms²

Solution: given, mass (m) = 5 kg

g = 10 m/s²

x = 10 m

we have been asked the potential energy (U) of the spring

as U = (1/2) k . x²

so, we will have to first obtain the value of k

as F = – k. x

F = mg

so, mg = – k. x

5 x 10 = k. 10

k = 5 N/m

putting the value of k and x in the equation of potential energy, we get

U = (1/2) x 5 x 10²

U = 250 joules

Sharing is caring!