How do I convert binary to decimal?

To convert a binary number to decimal we need to perform a multiplication operation on each digit of a binary number from right to left with powers of 2 starting from 0 and add each result to get the decimal number of it.

What is the 1111 binary to decimal?

15 is the decimal equivalent of the binary number 1111.

How do you write 0.75 in binary?

The decimal number 0.75 is written as 0.11 in binary.

What is 15 in binary form?

The binary equivalent of 15 is 1111.

How to Convert Binary to Decimal? -

Table of Contents

Binary to decimal conversion is a fundamental concept in computer science and digital electronics. The binary system, composed of only two digits—0 and 1—serves as the foundation for most computing operations, while the decimal system, using ten digits (0-9), is what we use in everyday life. Converting binary numbers to their decimal equivalents allows us to interpret and represent binary data in a more familiar format. This process involves understanding the place value of each binary digit and calculating the corresponding decimal value through powers of two. Mastering binary-to-decimal conversion is essential for programmers and engineers alike.

Binary to Decimal

A binary number (base-2) is converted to an equivalent decimal number using the binary-to-decimal conversion formula (base-10). In mathematics, numbers are expressed using a number system. It is a way to display numerical data. The four various number systems are as follows:

System of Binary Numbers (Base-2)
System of octal numbers (Base-8)
System of Decimal Numbers (Base-10)
System of Hexadecimal Numbers (Base-16)

The number system is crucial to computer systems. The number system is used by virtually all electronic devices, not just computer architecture. Therefore, learning how to convert between different number systems is crucial. Before we talk about converting from binary to decimal, let’s first grasp both number systems.

Binary Number System

A number that is employed in binary systems is referred to as a binary number system. The base 2 number system is another name for it. It uses two separate symbols to represent the numerical values, essentially 1 (one) and 0 (zero).

Decimal Number System

The base-10 numeral system is another name for the decimal number system. Ten digits, from 0 to 9, are used. The continuous locations to the left of the decimal point in the decimal number system stand in for units, tens, hundreds, thousands, and so forth. Consequently, 10 serves as the decimal number system’s base.

Binary to Decimal Conversion

When converting a binary number (base-2) to a decimal number, this process is known as binary to decimal conversion (base-10). Understanding binary-to-decimal conversion is crucial for applications using computer programming. Only two digits, 0 and 1, are used to represent the binary number system, whereas all ten digits, from 0 to 9, are used to represent the decimal number system. In the subsequent section, we must learn how to translate a binary number into its matching decimal number.

Know: Parts of Computer Name and Their Functions For Kids

How Binary to Decimal Converter Works?

We use the division method to multiply the binary integer to get its decimal equivalent. In this conversion method, each digit of the input number is multiplied from the Most Significant Bit (MSB) to the Least Significant Bit (LSB), lowering the base’s power, if a number with base n is to be turned into a number with base 10.

Binary to Decimal Conversion Steps

Write the specified binary number first, then count the powers of two going left to right (powers starting from 0)
Now, from right to left, write each binary digit with the matching powers of 2, so that the first binary digit (MSB) will be multiplied by the largest power of 2.
Add each of the items from the previous step.
The required decimal number will be the final response.

Check: Wi-Fi Full Form in Computer Network {English and Hindi}

Binary to Decimal Converter working Formula

We will learn the basic formula, let’s study how to convert a binary number to a decimal number. The formula to convert binary to decimal is provided as, where dn represents the digits of a binary number with ‘n’ digits.

The formula for conversing binary to decimal is given below

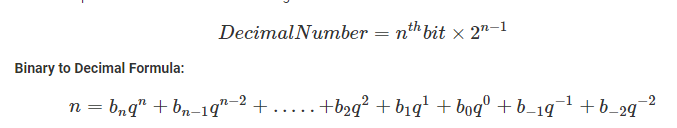
Where,

N is decimal equivalent,

b is the digit,

q is the base value

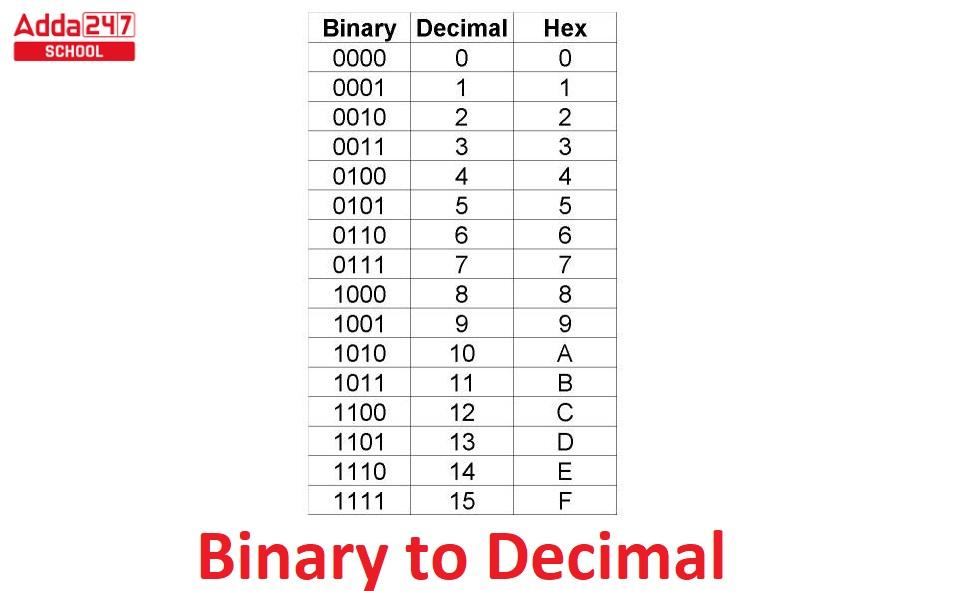
Binary to Decimal Table

Binary Number	Decimal Number	Hex Number
0	0	0
1	1	1
10	2	2
11	3	3
100	4	4
101	5	5
110	6	6
111	7	7
1000	8	8
1001	9	9
1010	10	A
1011	11	B
1100	12	C
1101	13	D
1110	14	E
1111	15	F
10000	16	10
10001	17	11
10010	18	12
10011	19	13
10100	20	14
10101	21	15
10110	22	16
10111	23	17
11000	24	18
11001	25	19
11010	26	1A
11011	27	1B
11100	28	1C
11101	29	1D
11110	30	1E
11111	31	1F
100000	32	20
1000000	64	40
10000000	128	80
100000000	256	100

Binary to Decimal Table

The conversion chart for Binary to Decimal conversion is given below

Binary	Decimal
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10
1011	11
1100	12

Binary to Decimal Conversion Examples

Example: Convert 1110₂, from binary to decimal using the binary-to-decimal formula.

Solution: We start doing the conversion from the rightmost digit, which is ‘0’ here.
(Decimal Number)₁₀ = (d₀× 2⁰) + (d₁ × 2¹)+ (d₂ × 2²)+ ….. (d_n-1 × 2^n-1),
= (0 × 2⁰) + (1 × 2¹) + (1 × 2²) + (1 × 2³)

= (0 × 2⁰) + (1 × 2¹) + (1 × 2²) + (1 × 2³)
= 0 + 2 + 4 + 8
= 14
Therefore, 1110₂ = 14₁₀

Example: Convert the binary number 1001 to a decimal number.

Solution: Given, binary number = 1001₂

Hence, using the binary-to-decimal conversion formula, we have:

1001₂ = (1 × 2³) + (0 × 2²) + (0 × 2¹) + (1 × 2⁰)

= 8 + 0 + 0 + 1

= (9)_₁₀

Example: Convert 1101001₂ into an equivalent decimal number.

Solution: Using binary to decimal conversion method, we get;

(1101001)₂ = (1 × 2⁶) + (1 × 2⁵) + (0 × 2⁴) + (1 × 2³) + (0 × 2²) + (0 × 2¹) + (1 × 2⁰)

= 64 + 32 + 0 + 8 + 0 + 0 + 1

= (105)_₁₀

1111 Binary to Decimal

1111 is in binary to decimal conversion is equal to 15.

1111

11111 Binary to Decimal

To convert the binary number 11111 to decimal, we can use the positional value of each bit. Starting from the right, each bit represents a power of 2, with the rightmost bit representing
2020.

1001 Binary to Decimal Conversion

In The binary conversion of 1001 means the 1 and the 8 bits are activated, but not the 2 or 4 bits. Thus, the binary-to-decimal conversion for 1001 is 8 + 1 = 9.