Area of Sphere
Area of Sphere all details are given in this article. The region covered by a spherical object’s surface in three-dimensional space is known as the area of sphere or total surface area of sphere. The curved surface area of the sphere is equal to the overall area of the sphere because it is a full curved shape. It’s sometimes referred to as lateral surface area.
Area of Sphere in Maths
A sphere is a solid shape that is bordered by a curved surface with every point on the surface being the same distance from the centre. In other terms, a sphere, like the surface of a round ball, is a fully round geometrical entity in three-dimensional space. The radius of a sphere is the distance between its centre and its outside surface. The surface area of a sphere is equal to 4r2 and is defined as the amount of territory covered by the sphere’s surface. The volume of a sphere is the amount of space it takes up in three dimensions.
A sphere is defined mathematically as a collection of points in three-dimensional space that are all at the same distance from a single point.
Area of Sphere Formula with Diameter
The surface area of a sphere in terms of diameter is given as, A=πD2 where “D” is the diameter of the sphere.
The radius of the sphere is the distance from the center to the outermost surface, while the diameter is the line that links two points on the sphere and is twice the radius’s length.
| Diameter = 2 x radius |
Area of Sphere Formula
Area of Sphere Formula given below.
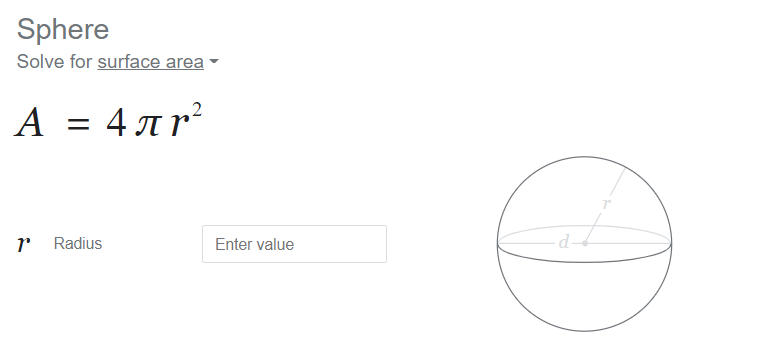
Area of Sphere Formula Derivation
Surface Area of the Sphere = Lateral Surface Area of the Cylinder
A cylinder’s lateral surface area is equal to 2 rh, where r is the cylinder’s radius and h is its height. Assuming that the sphere fits into the cylinder completely, the height of the cylinder can alternatively be thought of as the sphere’s diameter. Consequently, it is possible to state that height of the cylinder = diameter of sphere = 2r. Thus, the formula for the surface area of a sphere is surface area of sphere = 2rh, where ‘h’ can be replaced by the diameter, or 2r. Therefore, the sphere’s surface area is 2rh = 2r(2r) = 4r2.
Read More:
Area of Triangle
Area of Rhombus
Area of Parallelogram
Area of Sphere Formula is Equal to in Maths
area of sphere A is equal to
where r2= radius square
Properties of a Sphere
The following are some of the most important features of a sphere:
1. A sphere does not have a face or an edge.
2. A sphere is symmetrical in every way.
3. It isn’t a polyhedron at all.
4. The surface’s points are all equidistant from the sphere’s centre.
5. It just has one surface.
Surface Area of Sphere
The surface area of a sphere is a fundamental concept in geometry and is used in a wide range of applications, from engineering to physics. In this article, we will explore the formula for calculating the surface area of a sphere, as well as its properties and applications.
Formula of Surface Area of Sphere
The formula for the surface area of a sphere is given by 4πr², where r is the radius of the sphere. This formula is derived from the fact that the surface area of a sphere can be thought of as the sum of the areas of an infinite number of infinitesimally small circles. The constant 4π is the ratio of the circumference of a circle to its radius, and r² is the area of a circle with a radius of r.
It’s important to note that the surface area of a sphere is dependent solely on the sphere’s radius and not on the shape of the sphere. This means that a sphere of radius 1 has the same surface area as a sphere of radius 2, despite the fact that the latter sphere is twice the size of the former.
Surface Area of Sphere- Applications
The surface area of a sphere has a number of important applications in the fields of mathematics, science, and engineering. For example, in physics, the surface area of a sphere is used to calculate the amount of energy that is required to heat a spherical object. In engineering, the surface area of a sphere is used to calculate the strength of a spherical shell, such as a pressure vessel or a spherical tank.
In addition to its practical applications, the surface area of a sphere is also an important concept in mathematics, particularly in the field of geometry. For example, it is used in the study of the four-dimensional geometry of space-time, and in the study of the topology of three-dimensional manifolds.
Surface Area of Sphere
The surface area of a sphere is a fundamental concept in mathematics and science that has a wide range of applications. It is dependent solely on the sphere’s radius, and can be calculated using the formula 4πr². Understanding the surface area of a sphere is important in fields such as physics, engineering and mathematics, and is used in the study of the four-dimensional geometry of space-time and topology of three-dimensional manifolds.
The formula for calculating the surface area of a sphere is:
Surface Area = 4 * π * r^2
Where:
- π (pi) is a constant approximately equal to 3.14159
- r is the radius of the sphere
So, to find the surface area of a sphere, you need to square the radius and then multiply it by 4 times pi.
Surface Area of Sphere Formula
A sphere is a three-dimensional shape in which the total surface area of the figure is equal to the curved surface area. The curved surface area is the portion of the surface that is only covered by the curved component. The circular base is not taken into consideration in the formula.
The total surface area, on the other hand, is made up of the curved area as well as the base area. The formula for the sphere’s total surface area and curved surface area is given below.
| Surface area (TSA) = CSA = 4πr² square units |
Total Surface Area TSA of Sphere
The total surface area of a sphere can be calculated using the formula:
Where:
- is the total surface area of the sphere,
- (pi) is a mathematical constant approximately equal to 3.14159,
- is the radius of the sphere.
Make sure that the radius you use in the formula is consistent with the units you’re working with (e.g., if the radius is in meters, the area will be in square meters).
Curved Surface Area CSA of Sphere
The curved surface area of sphere is calculated using the formula 4πr², where r is the radius of the sphere. The constant 4π is the ratio of the circumference of a circle to its radius, and r² is the area of a circle with a radius of r. This formula represents the total area of the curved surface of sphere, and it is dependent solely on the sphere’s radius and not on the shape of the sphere.
It’s important to note that the curved surface area of a sphere is different from the total surface area of a sphere, which includes both the curved surface area and any flat areas, such as the base of a sphere. The curved surface area is the area of the outer surface of the sphere that forms a part of the sphere’s surface. This area of the sphere is always curved, and is used to calculate the amount of energy that is required to heat a spherical object, the strength of a spherical shell, and so on.
The curved surface area of sphere is the total area of its outer surface. It is given by the formula:
Curved Surface Area = 4πr^2
Where:
- π (pi) is a mathematical constant approximately equal to 3.14159.
- r is the radius of the sphere.
Keep in mind that the curved surface area only considers the surface area of the sphere itself, excluding the top and bottom “caps.” If you want to calculate the total surface area, including the caps, you would use the formula:
Total Surface Area = 4πr^2 + 2πr^2 = 6πr^2
This formula includes the curved surface area as well as the areas of the two hemispherical caps.
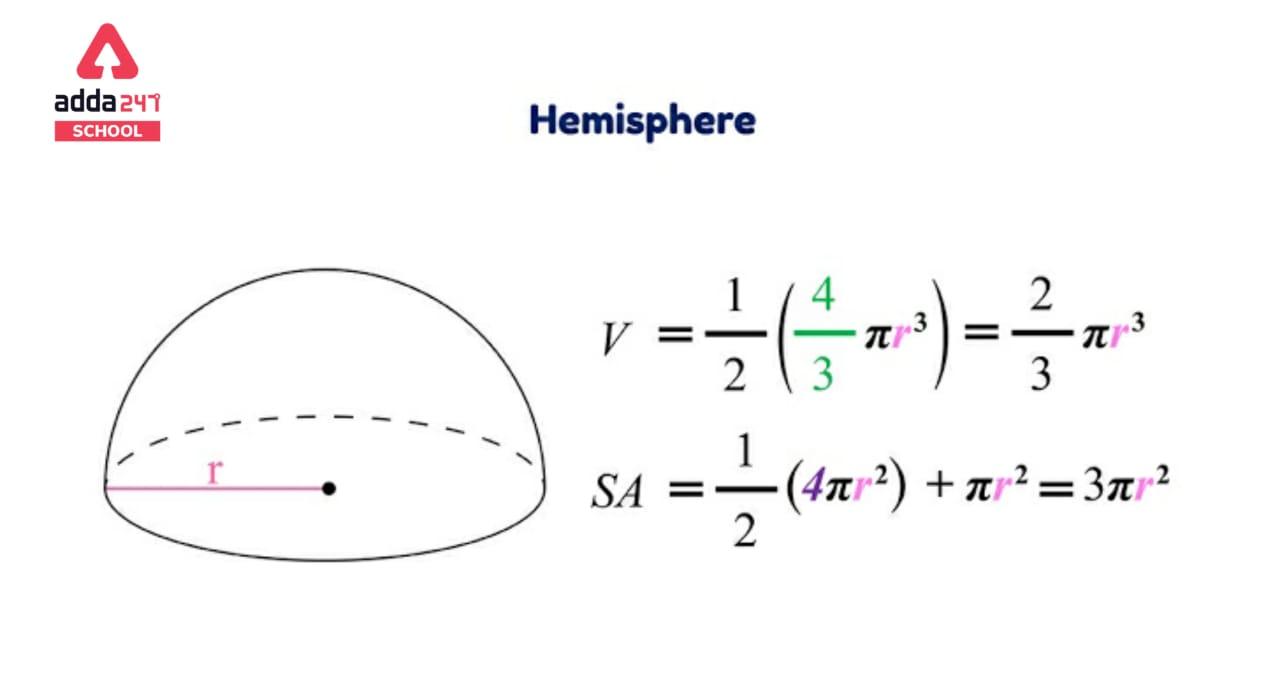
Area of Hemisphere
Hemisphere is a three-dimensional form that is half of a sphere. A hemisphere is formed when a plane divides a spherical into two equal half.
The sum of a hemisphere’s curved surface area and base area is its total surface area (TSA) (circular base).
- Total Sphere Area (hemisphere) = Half of area of sphere + Base area
- TSA = 2πr² + πr²
| TSA = 3πr² |
Area of Sphere- Sample Problems on Formula
Problem: Find the sphere of a sphere of diameter 12 m, rounding your answer to two decimal places (using pi = 3.14).
Soln: Diameter of the sphere (d) = 12 m
Finding the radius of the sphere,
- Radius of the sphere (r) = d/2 = 12/2 = 6 m
Area of the sphere (V) = 4 π r2
- V = 4 x 3.14 x 62
- V = 4 x 3.14 x 6 x 6
- V = 452.16
Therefore, the volume of the sphere is 904.32 m3 .
Problem: A plane passes through the centre of a sphere and forms a circle with a radius of 10 feet. What is the surface area of the sphere?
Soln: Radius of the sphere = 10 feet
Area of Sphere (A) = 4 π r2
- Area = 4 x 3.14 x 10 x 10
- Area = 1256
Therefore, area of the sphere is 1256 feet2.








 DTE Maharashtra Polytechnic Merit List 2...
DTE Maharashtra Polytechnic Merit List 2...
 JEECUP Round 2 Seat Allotment Result 202...
JEECUP Round 2 Seat Allotment Result 202...
 YCMOU Result 2025 Out @ycmou.digitaluniv...
YCMOU Result 2025 Out @ycmou.digitaluniv...









