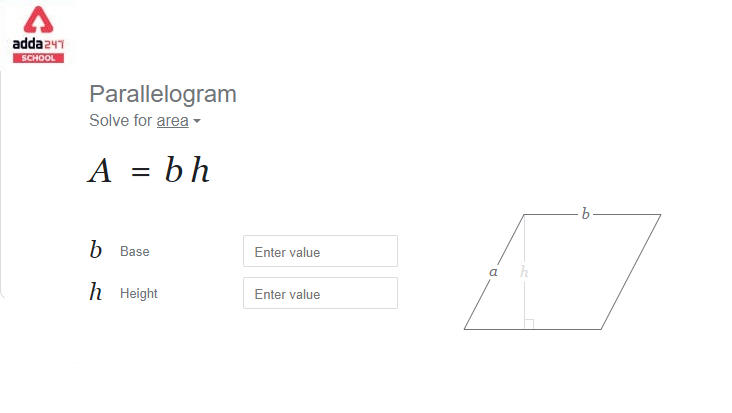
Area of Parallelogram
The area of a parallelogram in a two-dimensional plane is the area covered by a parallelogram. A parallelogram is a two-dimensional figure with four sides in geometry. It’s a type of quadrilateral with opposite sides that are equal and parallel. A parallelogram’s area is the space enclosed by its four sides. The area of a parallelogram is equal to the product of its length and height.
A quadrilateral’s internal angles add up to 360 degrees. A parallelogram is made up of two pairs of parallel sides that are of equal length. It has an area and perimeter because it is a two-dimensional figure. Let’s take a closer look at the area of a parallelogram, including its formula, derivations, and additional solved problems, in this post.
Area of Parallelogram Definition
In a two-dimensional space, the area of a parallelogram is the region bordered by the parallelogram. A parallelogram, as you may recall, is a specific form of quadrilateral with four sides, two of which are parallel. The opposite sides of a parallelogram are of equal length, and the opposite angles are of equal measure. The area of a rectangle is equal to the area of a parallelogram because the rectangle and the parallelogram have identical features.
Area of Parallelogram Formula
Multiply the perpendicular’s base by its height to get the area of the parallelogram. It’s worth noting that the parallelogram’s base and height are perpendicular to each other, but the parallelogram’s lateral side is not. As a result, the height is represented by a dotted line.
| Area of parallelogram = b × h square units |
Where b is the base and h is the height of the parallelogram.
Area of Parallelogram Finding Methods
- The area of a parallelogram can be computed using the base and height of the parallelogram. Aside from that, the area of a parallelogram can be calculated if its two diagonals are known, as well as any of their intersecting angles, or if the length of the parallel sides and any of the angles between them are known. As a result, there are three ways to calculate the area of a parallelogram.
Area of a parallelogram Formula From Rectangle Sides
Suppose a and b are the set of parallel sides of a parallelogram and h is the height, then based on the length of sides and height of it, the formula for its area is given by:
Area = Base × Height
A = b × h [sq.unit]
Area of a parallelogram Formula without height
If we don’t know the height of the parallelogram, we can apply the trigonometry idea to calculate its area.
Area = ab sin (x)
Where a and b are the length of parallel sides and x is the angle between the sides of the parallelogram.
Area of a parallelogram Formula using diagonals
The diagonal lengths can also be used to compute the area of any parallelogram. A parallelogram has two diagonals that intersect each other, as we all know. Assume that the diagonals cross at an angle of y, then the area of the parallelogram is given by:
Area = ½ × d1 × d2 sin (y)
Where, d1 and d2 are the lengths of the diagonals of the parallelogram.
Area of Parallelogram Formula Questions
Question 1: Find the area of the parallelogram with the base of 3 cm and height of 6 cm.
Solution: Base, b = 3 cm, height, h = 6 cm
As we know that,
Area of a Parallelogram = b×h Square units
= 3 × 6 = 18 sq.cm
Therefore, the area of a parallelogram = 18 cm2
Question 2: Find the area of a parallelogram whose breadth is 10 cm and height is 15 cm.
Solution: Breadth, b = 10 cm and height, h = 15 cm
Area of a parallelogram
= b × h
= 10 × 15 cm2
= 150 cm2
Question 3: The base of the parallelogram is thrice its height. If the area is 192 cm2, find the base and height.
Solution:
Let the height of the parallelogram = h cm
then, the base of the parallelogram = 3h cm
Area of the parallelogram = 192 cm2
Area of parallelogram = base × height
Therefore, 192 = 3h × h
⇒ 3 × h2 = 192
⇒ h2 = 64
⇒ h = 8 cm
Hence, the height of the parallelogram is 8 cm, and breadth is
3 × h
= 3 × 8
= 24 cm
Question 4: The area of a parallelogram is 128 sq.cm. Its height is twice its base. Find the height and base.
Solution: Area = 500 sq.cm. Height (h) = Twice of base (2b)
h = 2b
As we know by the formula that,
Area = b x h
128 = b x 2b
2b2 = 128
b2 = 64
b = 8 cm
Hence, height = 2 x b = 16 cm
Related Articles:
- Unit Of Force- What Is The SI & CGS Unit Of Force?
- CNG Full Form In Science And Medical
- Plaster Of Paris- Formula, Uses
- Bleaching Powder Formula And Chemical Name
- Rainbow Colours- What Is 7 Rainbow Colours In Order?








 BTEUP Result 2025 Out at bteup.ac.in, Do...
BTEUP Result 2025 Out at bteup.ac.in, Do...
 SGBAU Result 2025 Out, Check Summer Seme...
SGBAU Result 2025 Out, Check Summer Seme...
 How To Prepare for CUET Accountancy Exam...
How To Prepare for CUET Accountancy Exam...









