Angular Momentum Formula -Definition, SI Unit, Derivation, Examples

Angular Momentum Formula: The angular momentum formula neatly describes the concept of angular momentum. The angular momentum is analogous to the linear momentum in its linear motion counterpart. The angular momentum formula is one of the most widely used formulas which is used to solve many problems of the rotational dynamics. It finds many applications in different branches of physics. In this article, we will cover the different aspects of the angular momentum formula. 

Angular Momentum Formula

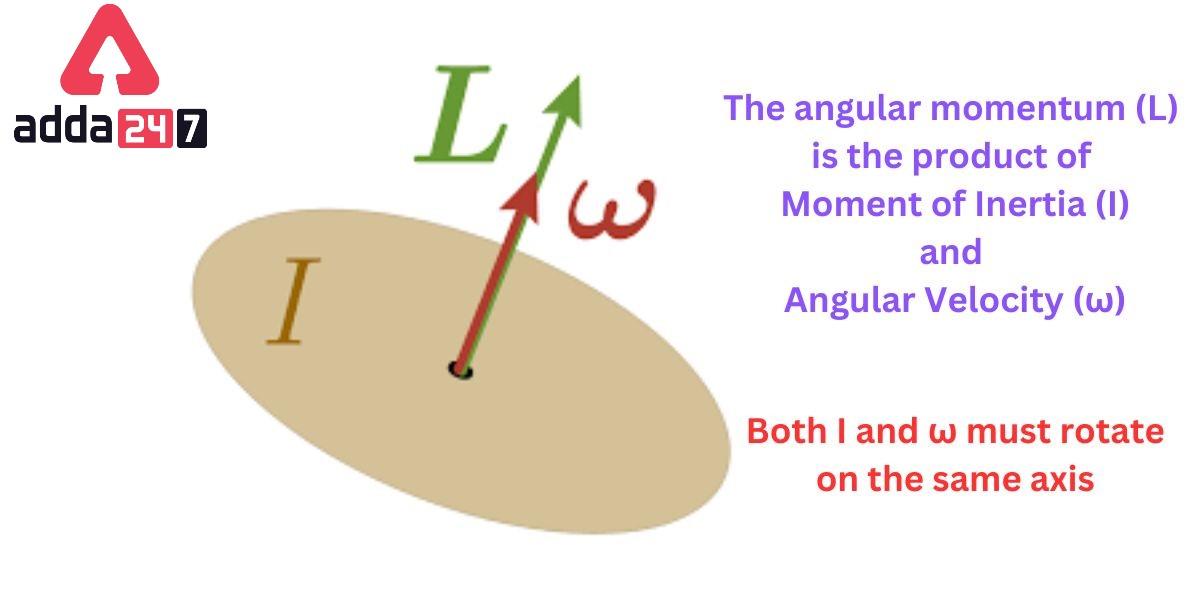
The rotational equivalent of the linear momentum formula is the angular momentum formula. Momentum is basically the product of mass and velocity in the linear momentum. Momentum tells us about the magnitude of impact a moving object can create. Using the angular momentum formula, we can calculate how challenging it is to alter the speed and direction of the object moving in a rotational motion. It is denoted by L. In essence, angular momentum is the result of an object’s moment of inertia and angular velocity.

The mathematical expression of the angular formula is given herein.

L = I x ω

Where ω is the angular velocity and I is the moment of inertia of that particular object

Another form of the angular momentum formula that is used primarily for point-sized objects is-

 L = P x r

Here, P is the linear momentum and r is the distance of the object from the axis of rotation, also known as the radius or radial distance. 

Angular Momentum Formula Derivation

The angular momentum formula is based on the second law of motion given by Newton. As the second law of motion deals with the concept of momentum, it helps in deriving the formula of angular momentum. As per Newton’s second law of motion, the net force acting on a body is equal to the rate of change of momentum. We can also derive the angular momentum formula using the angular momentum analogy of the linear momentum. The derivation of the angular momentum formula is given below.

As we know L = P x r—————(i)

Where L = angular momentum

P= Linear momentum

r = radial distance, i.e., the object’s distance from the axis of rotation

As P = m x v 

Here, m corresponds to the object’s mass and v corresponds to the object’s velocity

Putting these values in equation (i), we get

L = m x v x r—————–(ii)

As we know v = ω x r, where ω is the angular velocity

Putting the value of v as ω x r in equation (ii), we get

L = m x ω x r x r

Or, L = m x ω x r2————————–(iii)

As I = mr²

Where I is the moment of inertia

Putting this value in equation (iii), we get the formal angular momentum formula, i.e., 

L = Iω 

In the case of extended mass, the Σ mr2 will give the total value of inertia (I)

It is to be noted that both values (I and ω) must revolve around the rotation line, which is the same axis for both. 

Angular Momentum Formula SI Unit

The angular momentum formula helps us derive the SI unit of the angular momentum. Using the basic concept of the unit operations, we can derive the SI unit for the angular momentum formula. The same is highlighted below for a better understanding of students.

As L = Iω 

The SI unit I =  Kg m2

Si unit of ω = radian per second (s)

So the SI unit of L = Kg-m² x radian/s

As the radian corresponds to no unit, the SI unit of L becomes (Kg-m²)/s

Angular Momentum Dimensional Formula

As we have just extracted the SI unit of the angular momentum formula, we can now easily derive the dimensional formula of the angular momentum using that. The dimensional formula of the angular momentum is given below.

As SI unit of L = (Kg-m²)/s

Kg corresponds to M

M (meter) corresponds to L 

S (second) corresponds to T

So the dimensional formula of the angular momentum becomes [ML2T-1]

Angular Momentum Formula Quantum Number

Azimuthal quantum number, or secondary quantum number, and angular momentum quantum number are interchangeable terms. An atomic orbital’s quantum number, which also characterizes the orbital’s size and form, determines the angular momentum of the atom. The common value falls between 0 and 1.

Angular Momentum Conservation Rule

The conservation of the angular momentum is one of the most noteworthy properties of rotational motion. The conservation of angular momentum states:

Initial Angular Momentum = Final Angular Momentum

i.e., Linitial = Lfinal

This conservation rule explains occurrences like the increased spin caused by a figure skater pulling in their arms or the slowing down of a rotating item when its moment of inertia rises.

Angular Momentum Formula Solved Examples

The complex concept of the angular momentum formula will be best known to you if you thoroughly practice the solved examples given below. Apart from that, these examples will help you know the application of the angular momentum formula. 

Example 1: Determine the angular momentum of a pulley with a radius of 1 m and a mass of 20 kg that rotates at a constant speed of 6 rad/sec.

As given in the question, 

Mass (m) = 20 kg
Angular Velocity (ω) = 6 rad /s
r = 1 m 
As we know Angular Momentum (L) = Iω 
I = ½ x mr² for pulley 
So, I = 20 x 1 x 1 = 20 Kg-m²
Putting the value of I in the equation of angular momentum, we get:
L = 20 x 6
L = 120 Kg-m²/s

Example 2: The angular momentum of a hoop with a mass of 10 kg and a radius of 1 m is 50 Kg-m²/s. Determine the hoop’s angular velocity.

As we are given with the angular momentum (L) = 50 Kg-m2/s
Mass (M) = 10kg
Radius (R) = 1 m
The moment of Inertia of a hoop is given by:
I =  MR²
I = 10 x 1 x 1
So, I = 10 Kg-m²
As L = Iω 
50 = 10 x ω
Or, ω = 50/10
ω = 5 rad/s   

Example 3: On the ice, a figure skater is turning. She weighs 80 kg, and because her arms are outstretched, her moment of inertia is 5 Kg-m2. She is rotating with a 20 rad/s angular velocity. Her angular momentum is what?

Here we are provided with the value of the moment of Inertia (I) = 5 Kg-m2 

Angular Velocity (ω) = 20 rad/s

So applying the angular momentum formula:

L = Iω 

Putting the given values, we get

L = 5 x 20

L = 100 Kg-m2/s

The angular momentum formula is an effective tool for comprehending and forecasting the rotational motion of objects.

Sharing is caring!