Angle of Elevation- Definition, Formula, Diagram, Examples

Angle of Elevation: Whenever you look upward in the sky or at the top of a building, you are unknowingly forming an angle of elevation. This angle is an important concept in the geometrical world. It is one of the most important concepts that is widely used in real-world engineering. It is an important tool to solve complex spatial problems related to height and distance. This angle is associated with viewing objects present at an elevated height. Through this article, we will explore different aspects of this crucial angle and understand its applications.

Angle of Elevation

As the name suggests, the angle of elevation is created when we observe anything that is located at a greater height than us. The concept of this elevation angle is used to find out height and distance, especially in trigonometry. This angle is created whenever we observe an object above the surface. For example, when we view the terrace of our building from the ground, this angle is formed with respect to our eyesight. As the name says, it is formed in such a way that it is above the observer’s eye.

What is the Angle of Elevation?

The formal definition for the angle of elevation states that it is an angle formed between the line of sight of the observer and the plane/line horizontal to the observer’s eye in the still position. In other words, the elevation angle is the angle formed at the intersection of the direction in which the observer views an object at an elevated position to the direction in which the observer sees during the head-still position in the horizontal direction. This can be better understood through an analogy.

Think about a ladder leaning against the wall. In that case, the angle formed by the foot of the ladder with the ground is known as the angle of elevation. By extending this analogy, we can consider the horizontal line to be the ground and the ladder to be the line of sight.

Angle of Elevation Diagram

If you are still uncertain about the position of this angle, the following diagram will clear the air for you. The diagram given below will make you understand this angle and will help you picturize this concept in your memory.

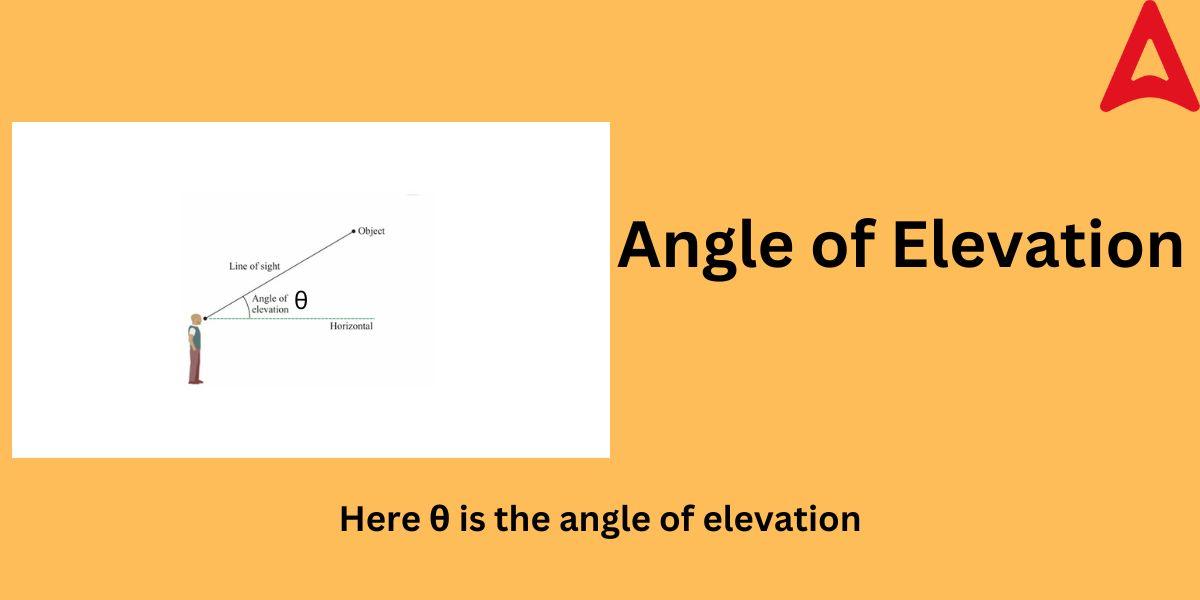
As you can see in the above figure that a person standing is looking at an elevated object, i.e., the object situated above the horizontal line of its eye.

The angle θ in the above diagram denotes the elevation angle.

You can clearly observe that the angle θ is formed between the line of sight and the horizontal of the observer.

Angle of Elevation Explanation

The angle of elevation is always formed above the eye of the object. It is formed when you view the sun or an airplane flying in the sky. As discussed in its definition above, this angle is formed between the line of sight and the horizontal line. What basically are these two terms. To understand the angle of elevation fully, first we will have to get acquainted with these technical terms.

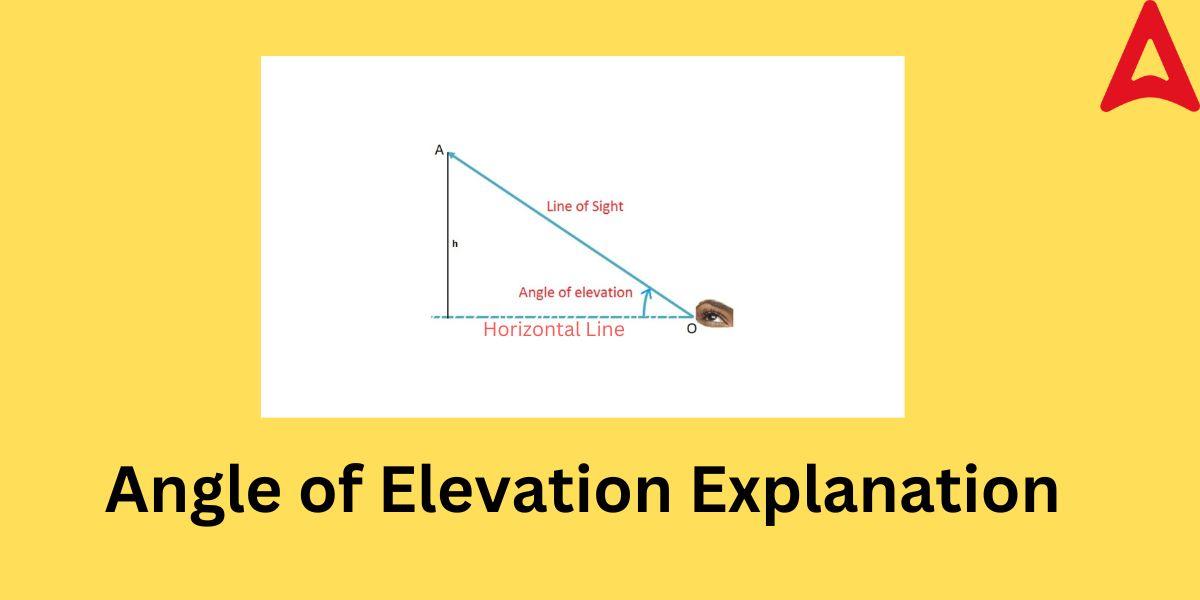
Line of sight: It is an imaginary line that is drawn from the eye of the observer to the object that is viewed at a greater height. In simple words, it is the direction in which the observer is viewing the object. We can obtain this point by taking the observer and the object as points on a plane and joining these two points with a straight line.

Horizontal line: It is a straight imaginary line on the plane that has a fixed y co-ordinate. That is, the x co-ordinate changes in the horizontal line but the y co-ordinate remains constant. In simple words, it is an imaginary line that is drawn from the eye of the observer in still position parallel to the ground/surface.

These terms have been shown in the following figure so that students can understand them better.

Angle of Elevation Formula

We can find the value for this special angle by using its formula. We can find the value for the elevation angle by knowing some of the measures. We can find the angle of elevation formula by knowing any of the two values from the height (length of the observed object from the horizontal line), horizontal length (length of the base of height from the observer), and the line of sight (hypotenuse). The formula is given by:

Tanθ = height/horizontal length

Sin θ = height/line of sight

Cos θ = horizontal length/line of sight

where, θ is the angle of elevation.

Angle of Elevation of the Sun

The rising and setting of the sun is a phenomenon that we observe daily. As sun is located far above from us, whenever we view it, we form an elevation angle in doing so. There is an interesting relation existing between the position of sun and the elevation angle formed. During the sunrise, when the sun is farthest from us, the the value of the angle of elevation is minimum. As sun keeps on rising, the angle’s value keeps increasing. It reaches its highest value during the noon period, when the sun is straight ahead of our head. At that time, the elevation angle of the sun with respect to the observer becomes 90°. After that the elevation angle starts decreasing and reaches its minimum value during the sunset.

Angle of Elevation properties

There are some unique properties associated to the angle of elevation. These properties will help students in solving various trigonometric problems related to height and distance.

• This angle is always formed when we see an object located above our height
• The elevation angle of the sun becomes maximum during the noon
• The maximum value of the for this angle can be 90°
• It is also known as upwards angle
• The object is above the horizontal line

Angle of Elevation Applications

This special angle finds many applications in the real world. Some of its applications are mentioned below.

• Maps and cross-sections of a landscape can be made using the elevation angle at various sites.
• For artillery and other weapons, firing solutions can be calculated using the angle of elevation to enemy targets.
• It is possible to calculate latitude and longitude using the elevation angle formed with the sun or other stars.
• To calculate the distances and velocities of various celestial objects, including planets and stars, one can use the this angle to those objects.

Angle of Elevation Examples

Below we have given some of the solved examples on this topic so that students can have a better grasp on this subject. These solved questions will be very useful for students of class 10.

Example 1: Determine the height of the building if an observer standing 50 meters away from a structure measures the elevation angle to the top of the structure at 30°.

Solution: We have been given,

angle of elevation (θ) = 30°

horizontal length = 50 meter

we have been asked to find the height of the structure

Using Tanθ = height/horizontal length

Tan 30° = height/50

1/√3 = height/50

height = 50/√3

Hence, the height of the structure = 50/√3

Example 2: A pilot is cruising at 5,000 meters in the air. She calculates a mountain’s height angle to be 45°. How far is it from the cockpit to the mountain?

Solution: As mentioned in the given problem,

height = 5000 meters

angle of elevation = 45°

we have to find the distance of the mountain, i.e., the horizontal length

Using Tanθ = height/horizontal length

Tan 45° = 5000/horizontal length

1 = 5000/horizontal length

horizontal length = 5000

Hence, the distance of the mountain from the cockpit = 5000 meter

Example 3: The length of the line of sight from the object to the observer is 300 meter. If the object is located at the height of 150 meter, the find its elevation angle.

Solution: As we have been given,

line of sight length = hypotenuse = 300 meter

height of the object = 150 meter

Let the elevation angle be θ

Then, Sin θ = height/line of sight

Sin θ = 150/300

Sin θ = 1/2

or, θ = 30°

Hence, the elevation angle= 30°

Sharing is caring!