Co-Interior Angles: Meaning, Theorem, Property, Examples

When a traversal intersects the two parallel lines, one of the angles created by it is the Co-Interior angle. These angles are one of the special types of angles formed at the juncture of the traversal and parallel lines. These angles show many different features that find many uses in the geometrical world. These angles are always formed between two parallel lines. Apart from these special angles, many different types of angles are formed by the traversal like alternate angles, corresponding angles, and vertically opposite angles. In this article, we will explore its definition, properties and many other aspects that are important for students to learn.

Co-Interior Angles

Co- Interior angles are formed on the same side of the traversal. It can be thought of as of the opposite nature of the alternate interior angles in which the angles are located on the different sides of the traversal. These angles are located inside the boundary of two parallel lines. These angles always exist in pairs and exhibit some unique features. When a traversal line intersects the two parallel lines, these angles are formed on the same side of the traversal. Let us understand these special angles through their definitions and diagrams.

Co-Interior Angles Definition

Co-Interior angles are the angles formed by the two parallel lines and a traversal that is situated on the same side of the traversal within the boundary of the two parallel lines. These angles are supplementary in nature, i.e., the addition of the angles results in 180°. In other words, these angles are angles situated inside the parallel lines on the same sides of the traversal whose sum is equal to 180°. Their angles can supplement one another, i.e., they form a supplementary pair. The diagram given below will help you better understand these angles and will tell you their position in the plane of the traversal.

Co-Interior Angles Diagram

The diagram given below shows the two pairs of these special angles. As shown below, these angles are located on the same side within parallel lines.

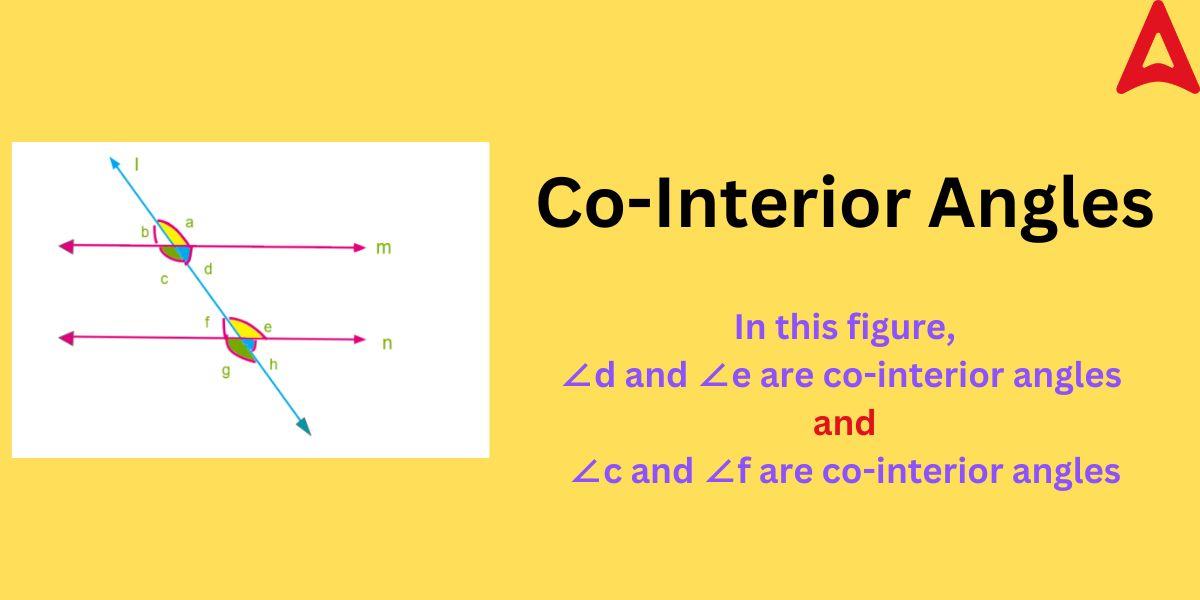
As shown in the above figure,

“m” and “n” are the two parallel lines

“l” is the traversal which intersect these two parallel lines

The two pairs of angles that are co-interior in the given figure are:

∠e and ∠d

∠f and ∠c

Co-Interior Angles Full Form

The co-interior angles is a short form of the consecutive interior angles. So, the full form of these angles is consecutive interior angles. As the name suggests, these angles lie consecutively, i.e., one after the other. This is evident from the above diagram that these angles lie at consecutive positions on the same side of the traversal in between the two parallel lines.

Co-Interior Angles Sum

As these angles lie on the same side of the traversal, so they form a straight line. From the property of the straight line, we can say that the sum of the angles forming a straight line must be 180°. So, the sum of consecutive interior angles is always equal to the measure of a straight angle, i.e., 180°.

Co-Interior Angles Supplementary

As we know that supplementary angles are those angles whose sum is 180°. It is already stated above that the sum of consecutive interior angles equal 180°, so we can say that these angles are supplementary angles. The individual angles of this pair are supplement to each other.

Co-Interior Angles Formula

As we know the basic features of these angles, we can derive its formula. The formula is used to find the missing angle from the pair of these angles. The formula is given below.

As we know that sum of consecutive interior angles = 180°.

Let us suppose one angle in the pair = X

So the missing angle = 180° – X

Co-Interior Angles Theorem

The theorem for the co-interior angles states that the sum of the successive internal angles pair on the same side of the traversal between the two parallel lines equals 180°. In simpler words, the sum of these angles is equal to 180° or these angles are supplementary angles. The proof of this theorem is stated below:

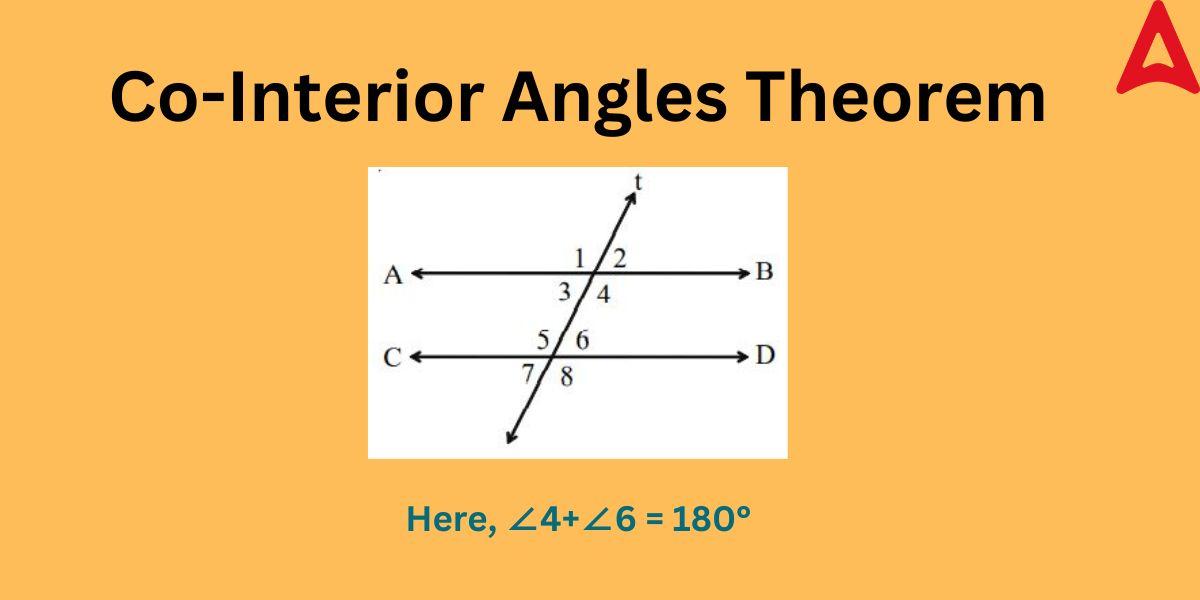
As given in the above figure,

AB and CD are parallel lines and t is the traversal

We have to prove the sum of consecutive interior angles, i.e., ∠4 +∠6 =180°

As ∠2 +∠4 =180° (linear pair of angles) ———-(i)

∠8 +∠6 =180° (linear pair of angles) —————(ii)

∠2 = ∠6 (corresponding angles)

∠4 = ∠8 (corresponding angles)

Substituting ∠2 and ∠8 with angle ∠6 and ∠4 respectively in the above equations, we get

∠6 + ∠4 =180°

∠4 + ∠6 = 180°

On adding the above two equations, we get

2 (∠4 + ∠6) = 360°

∠4 + ∠6 = 180°

Hence proved

Co-Interior Angles Property

Consecutive Interior angles (Co Interior angles) are one of the special types of angles that is highly useful in explaining different concepts of angles. Its features will prove to be beneficial for students in solving complex problems in geometry. Some of its unique features are:

• They are located consecutively on the same side of traversal within the parallel lines
• Their sum equals 180°
• There are only two pairs of angles present in a single traversal
• These angles are supplementary in nature
• They are equal to each other only when the traversal cuts the parallel lines perpendicularly

Co-Interior Angles Examples

The solved examples mentioned below will provide a clear understanding of this topic. Students will be able to apply this concept in a more fruitful manner after understanding the examples given below.

Example 1: The values of angles situated on the same side of the traversal inside the parallel lines are 4X-23° and 6X-17°. Find the value of X.

Solution: As we know that angles situated inside the parallel lines on the same side of the traversal are consecutive interior angles (co interior angles).

So, using its supplementary property

4X-23° + (6X-17°) = 180°

4X-23° + 6X-17° =180°

10X – 40° = 180°

10X = 220°

Hence, X = 22°

Example 2: If the value of one of the angle in a consecutive interior angles is 46°. What will be the value of other angle?

Solution: As we know sum of consecutive interior angles = 180°

So, 46° + other angle = 180°

other angle = 180° – 46°

Therefore, other angle = 134°

Example 3: If the value of two consecutive interior angles are 80° and 60°+a, what will be the value of a?

Solution: By using its sum property

80° + 60°+a = 180°

140° + a = 180°

a = 180°-140°

a = 40°

Sharing is caring!