Alternate Interior Angles- Definition, Theorem, Diagram, Examples

Angles are one of the most fundamental entities in geometry which is present in every branch of it and one such special type of angles are alternate interior angles. It is one of the two types of alternate angles found in the mathematical world. Alternate angles are a concept associated with the parallel lines and the traversal. Due to its unique nature, it finds a special place in the mathematical world. The definition and theorem of these special angles will be covered in detail in this article along with illustrated examples.

Alternate Interior Angles

One of the angles created when a transversal intersect two coplanar lines are known as alternate interior angles. These angles are located on the opposing sides of the traversal line and on the inner sides of the two parallel lines. Apart from these angles, other types of angles formed by the two parallel lines and a traversal are alternate exterior angles, corresponding angles, and vertically opposite angles. The transversal cuts through the two lines that are coplanar at two different locations. These angles can be used to show that the two coplanar lines are parallel to each other. If these angles are equivalent, then the lines that the transversal crosses are parallel.

Alternate Interior Angles Definition

As per the formal mathematical definition, alternate interior angles are those angles that are formed at the intersection of traversal with the two parallel lines on the opposite sides of the traversal and on the inner sides of the parallel lines. In other words, we can say these angles are the non-adjacent angles that are formed on the inner sides of the parallel lines. This special angle pair is always equal in nature. So we can also say that if the pairs of this angle is equal, then the lines must be parallel. Let us understand this concept more clearly through a diagram.

Alternate Interior Angles Diagram

A diagrammatic view of these angles will help you get a clear idea about the position of these angles. The below diagram shows various angles formed when the traversal intersect the two parallel lines.

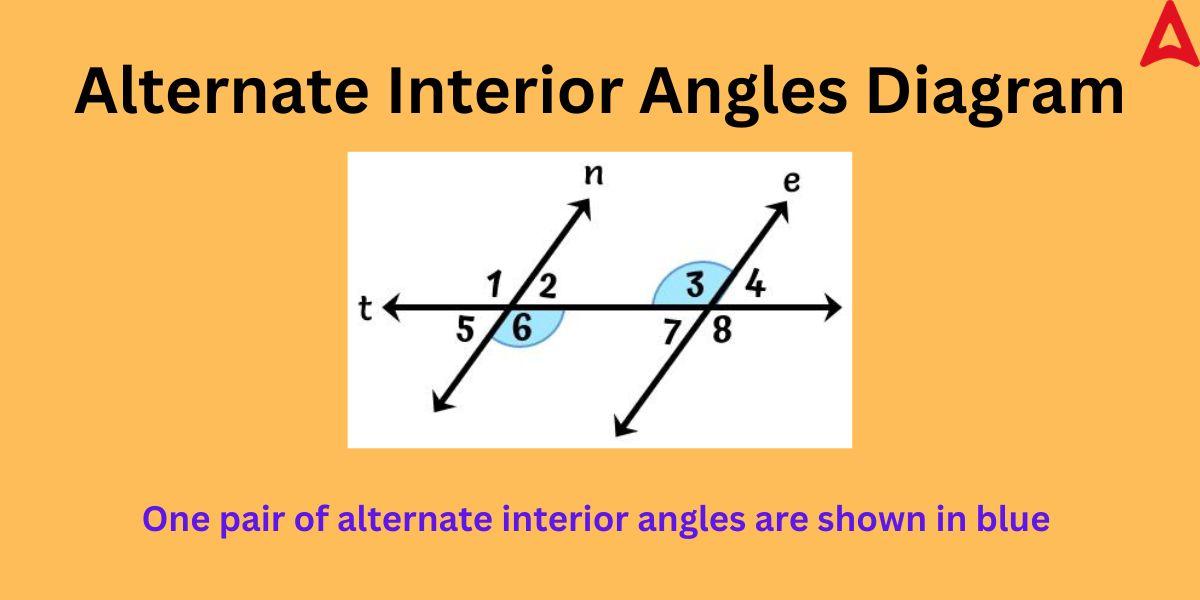
From the above figure,

the two parallel lines are “e” and “n”

the traversal is “t”

The pairs of alternate interior angles are:

∠6 and ∠3

∠2 and ∠7

As one can observe from the above figure that the pairs of these special angles are situated at the opposite sides of the traversal and enclosed within the two parallel lines.

Alternate Interior Angles are Equal

It is utmost importance to note that the measure of these angles are equal. The pairs are congruent to each other. If these two angles are not equal then it must be noted that the two lines that the traversal intersect are not parallel. The two parallel lines and a traversal always produce such pairs of these angles that are congruent, i.e., equal in measure. This feature is very important and is used to prove the parallel nature of two lines.

Alternate Interior Angles Supplementary

The sum of these angles can be supplementary in a special case. These angle pairs are supplementary when the traversal cuts the parallel lines in perpendicular. That is, if the angle between the traversal and the two parallel lines is 90°, the these pairs add up to give supplementary angles. In this case, each angle in the pair equals 90°. Hence, their sum is equal to 180°, i.e., supplementary. In other cases, these angles do not form the supplementary pair.

Alternate Interior Angles in a Triangle

The concept of the these angles can be also visualized in a triangle. This angle-pair is formed in a triangle when a parallel line if drawn touching a vertex that is parallel to the opposite side of the vertex. In such case the exterior angles situated on the parallel line drawn forms this special angle pair with the two angles situated on the other opposite side of the triangle. This concept can be easily understood through the diagram given below.

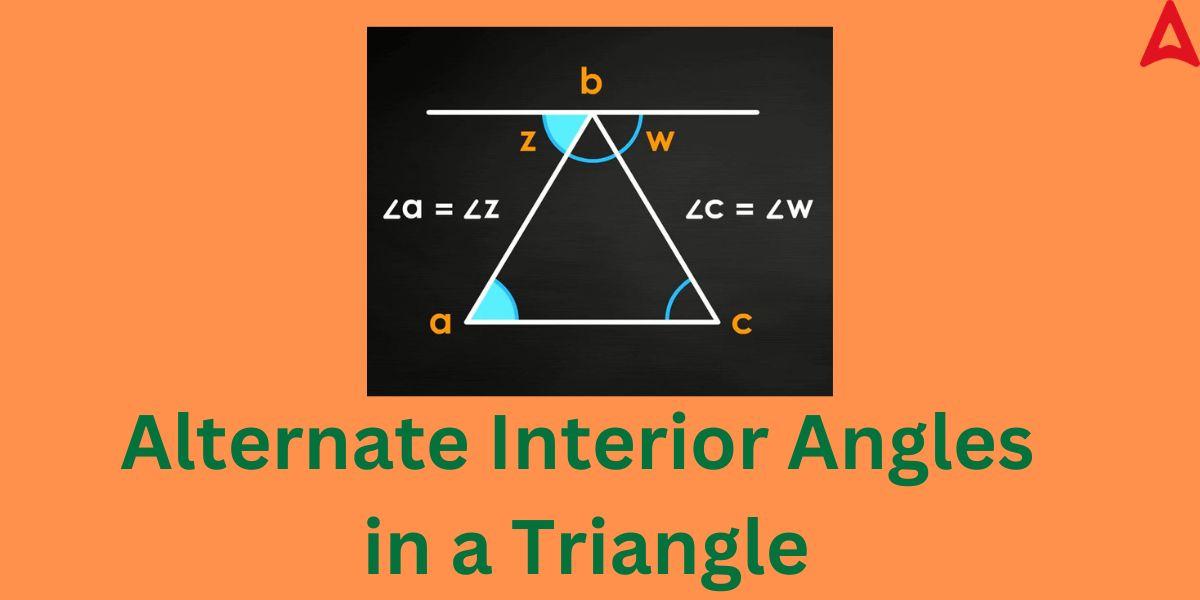
In the above figure, a parallel line is drawn through vertex b that is parallel to the side ac that is opposite to the vertex. The angle pairs situated at the opposite parallel sides, i.e. ∠a and ∠c forms an alternate interior angle pair with angle w and angle z respectively. Angle w and angle z are exterior angles for the triangle ABC. These angle pairs are equal to each other, i.e. congruent. So, from the above figure, we can conclude that the alternate interior angles in the given triangle are:

∠a = ∠z

∠c = ∠w

Alternate Interior Angles Theorem

The theorem of this angle states that the alternate interior angles are equal in measure, i.e., congruent if a transversal cuts through the pair of parallel lines. The proof of this theorem is given below.

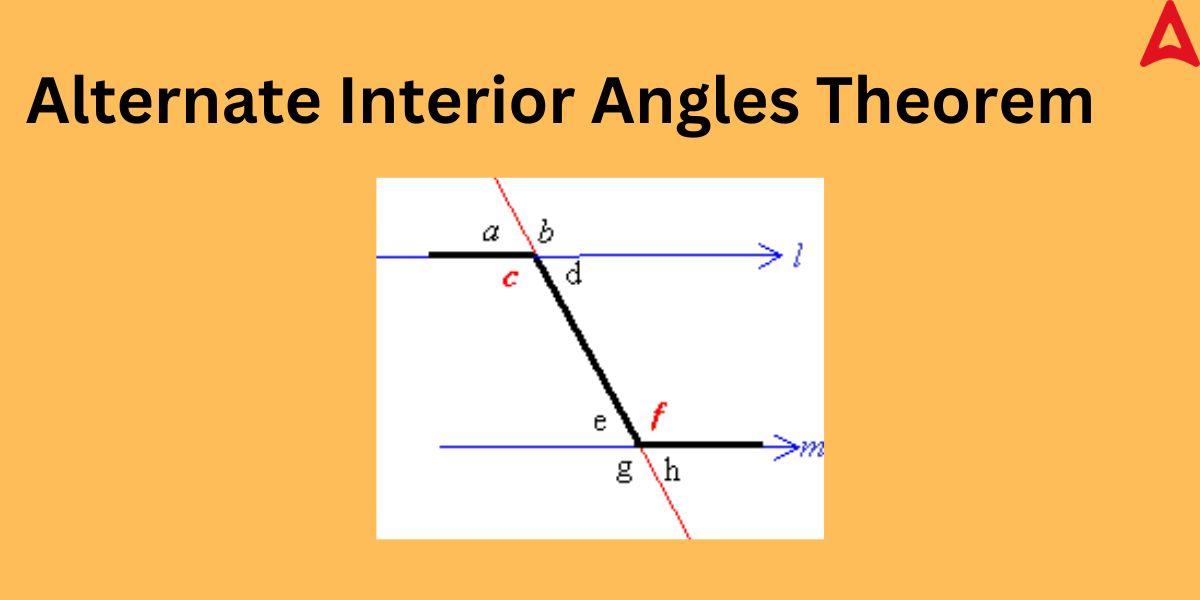
Proof: In the above given figure, “l” and “m” are two parallel lines

we have to prove that ∠c = ∠f

As given in the figure:

∠c = ∠b (vertically opposite angles) ———–(i)

also, ∠f = ∠b (corresponding angles) ———-(ii)

on comparing equation (i) and equation (ii), we can conclude that

∠c = ∠f, which are interior angles that are alternate

The converse of this theorem also holds true. That is, if the alternate interior angles are congruent (equal) then the lines must be parallel.

How to find Alternate Interior Angles

We can find the the value of these angles using its property that they are congruent or equal in nature. So if one of the angle from the pair is given, we can easily find the other pair. The other way to find the value of these angles are that it satisfy the following two conditions:

1. The angles are situated on the inner side or parallel lines
2. They are located on the opposite ends of the traversal

Alternate Interior Angles Properties

These angles possess some special properties that help students to differentiate these angles from others. Some of the properties of this special angle is given below.

• They are always equal in measure, i.e. congruent
• There are always two pairs of these angles in between the two parallel lines
• These angles can be supplementary if the traversal cuts the parallel lines at perpendicular

Alternate Interior Angles Examples

Some of the solved examples of the alternate angles are given below. These solved questions is important from the examination point of view. After understanding these solved examples, students will have a better grasp on this segment of angles.

Example 1: The values of two alternate angles (interior) are given as 7a+3 and 8a-27. What will be the value of a?

Solution: As we know that alternate interior angles are equal in measure

So, 7a+3 = 8a-27

=> 27+3 = 8a – 7a

Hence, a = 30

Example 2: If the value of one of the interior angle that is alternate is 56° and the value of other angle in the pair is 17°+Y. Find out the value of Y.

Solution: As we know, alternate angles (both interior and exterior) are equal in nature

So, 17°+Y = 56°

=> Y = 56° – 17°

Hence, Y = 39°

Sharing is caring!