Angle of Deviation: Definition, Diagram, Formula, Examples

The angle of deviation is a special phenomenon related to the property of light. It is one of the most important concepts in the world of optics. This special angle explains various physical phenomena of light. This angle is observed when a ray of light passes through the prism. All physics enthusiasts must have noticed the picture of the great Newton holding a prism in his hand. Thus, in the world of optics, this angle plays an important role primarily in the case of prisms.

Angle of Deviation

In optics, the angle of deviation is an important phenomenon, especially when working with prisms. Refraction occurs when light travels through a prism, causing the light path to change. The angle of deviation, also called deviation angle, takes place due to the process of refraction in prisms. It is essential to appreciate this special angle in order to develop optical systems and to understand how light behaves when it interacts with transparent materials. Let us understand this concept in more detail through its definition and a diagram.

Angle of Deviation Definition

The deviation angle is the angle formed between the direction of the incident ray and the direction of the emergent ray. In other words, the difference in angle between the initial route that the beam ought to have taken and the deviated beam is known as the angle of deviation. It can also be described as the angle at which an incident ray deviates from a straight path after passing through a prism. The degree of deviation depends on the wavelength of the light and the refractive index (n) of the material. Let us understand this angle through a diagram so that you can get a clear picture of it in your mind.

Angle of Deviation Symbol

Just like any other physical quantity, the deviation is too denoted by a symbol. The symbol for this angle helps in identifying this angle and saves the time to write its complete name again and gain. The symbol for this special angle is δ (delta). It is pronounced as delta and it is a Greek symbol.

Angle of Deviation Diagram

The below figure shows the the deviation angle.

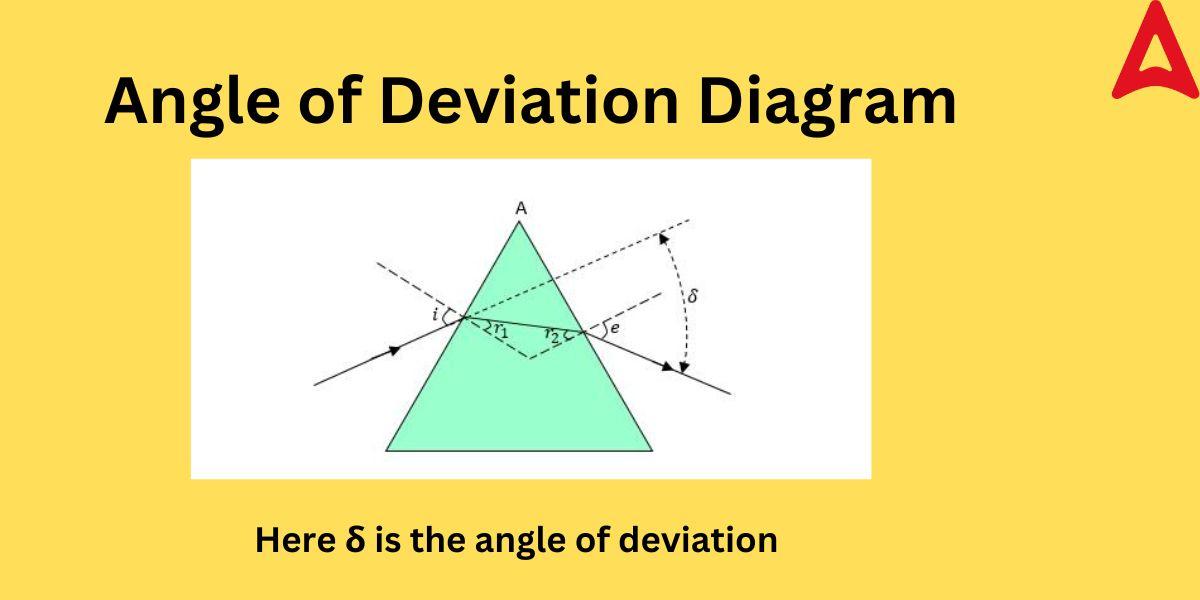
In the above figure a cross-section of the triangular prism is shown.

As you can observe from the given figure, the ray of light deflects its path after entering the prism at an angle “i” (angle of incidence) and leaving the prism at angle “e” (angle of emergence).

Here the deviation angle is shown by δ.

Angle of Deviation in Prism

The deviation phenomenon of the light is observed clearly in the prism. The passing of light through a prism causes it to deviate it from its original path, hence forming the angle of deviation. A wedge-shaped body constructed of a refracting material is referred to as a prism. Two plane faces that are positioned at an angle to one another and set at an incline serve as its boundaries. The prism’s two flat faces are referred to as the refracting faces. The angle of the prism is the angle formed by the two faces. The refracting angle is another name for it. The light undergoes refraction at both faces of the prism.

Angle of Deviation Formula

The deviation angle’s formula is very important as it interconnects various angles of prism. It is relation which shows the relationship between angle of incidence, angle of prism, angle of emergence, and the deviation angle.

The angle of deviation formula is given by:

δ = i + e – A

where, δ is the angle formed due to the deviation

i is the angle of incidence

e is the angle of emergence

A is the prism angle

Angle of Deviation Derivation

The formula mentioned above can be derived using some basic concepts. Let us derive this formula with the help of a diagram.

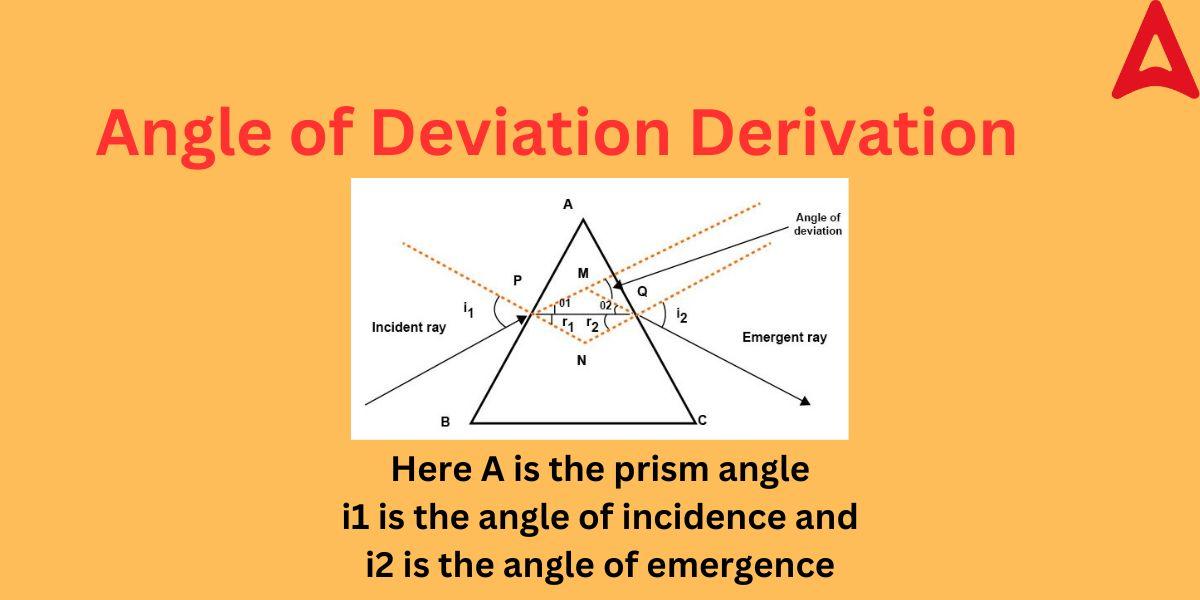
In the above figure, we can observe that the incident ray entering and leaving the triangular prism.

From the above figure,

The deviation angle in the above case is formed at vertex point M

The angle of incidence is given by i₁

The angle of emergence is given by i₂

The prism angle is denoted by A

Let the deviation angle be denoted by δ

By observing the constructions of angles in the above figure and using elementary analysis, we can say that

δ = i₁– r₁ + i₂ – r₂

or, δ = (i₁+i₂) – (r₁+r₂)

From the triangle PQN, we can say that,

∠N = 180° – (r₁+r₂)

As we know, ∠APN = ∠AQN = Normal = 90°

Now, in quadrilateral APNQ

∠A + ∠P + ∠N + ∠Q = 360° (angle sum property of a quadrilateral)

Substituting the value of ∠P and ∠Q as 90° (normal)

∠A + 90° + ∠N + 90° = 360°

∠A + ∠N + 180° = 360°

∠A + ∠N = 360° – 180°

∠A + ∠N = 180°

As ∠N can be written as 180° – (r₁+r₂)

Substituting this value of ∠N in the above equation, we get

∠A + 180° – (r₁+r₂) = 180°

or, ∠A = (r₁+r₂)

Using the value of angle A from triangle ABC, we get

δ + A = i₁+i₂

or, δ = i₁+i₂ – A

Angle of Deviation and Angle of Incidence Graph

There is a relation between the deviation angle and the angle of prism. The relation can be represented graphically. The graphical representation of this relation is shown below.

As you can observe in the above diagram, at a particular angle of incidence, the deviation of the light becomes minimum for a particular wavelength of light, hence giving the minimum deviation angle value.

Minimum Angle of Deviation

When we keep on increasing the angle of incidence, the deviation angle keeps on decreasing. After a particular lowest point, the deviation angle starts increasing again. After this lowest point, the value of this angle keeps increasing on increasing the incidence angle. This lowest angle angle value is known as the minimum angle of deviation. The minimum angle formed due to deviation remains constant for a particular material at a particular wavelength of light. The minimum angle of the deviation is denoted by δ_m. The relationship between the refractive index of the material and the minimum deviation angle is denoted by the following formula.

The minimum angle of deviation is given by

n = Sin((A+δ_m)/2)/Sin(A/2)

where, n = refractive index of the material

A = Prism angle

δ_m = minimum deviation angle

Angle of Deviation Depends on

It must be noted that the angle of deviation changes with the changing surrounding condition. It depends on:

• The wavelength of light used
• The angle of incidence
• The prism angle
• The refractive index of the material

Angle of Deviation in Mirror

The concept of the deviation angle can also be applied in the mirror. As we know that light rays get reflected from the mirror surface. But if we trace the path of the incident light rays behind the mirror, then the angle formed between the imaginary light ray and the reflected light ray is known as the angle of deviation in mirror. For a plane mirror, the deviation angle is always the twice value of the angle of incidence. Mathematically,

δ = 2i

where, δ is the deviation angle in the case of mirrors

i = angle of incidence

Angle of Deviation Examples

The angle of deviation concept is very important for class 10 and class 12 students. So they must have a clear understanding of this particular topic. The following solved questions will help students in understanding this concept in a better way.

Example 1: A prism is given with the value of the prism angle as 50°. The angle of incidence is given to be 35° and the angle of emergence is given to be 40°. Find out the value of the deviation angle.

Solution: As we know that the deviation angle is related to the prism angle, angle of incidence and the angle of emergence by the formula:

δ = i + e – A

given, A = prism angle = 50°

i = angle of incidence = 35°

e = angle of emergence = 40°

putting these values in the formula, we get

δ = 35° + 40° – 50°

δ = 75° – 50°

δ = 25°

Hence, the deviation angle = 25°

Example 2: Find the refractive index of the prism if the angle of minimum deviation of a light beam passing through it is 30° and the prism angle is 60°.

Solution: As we have been given

prism angle = A = 60°

minimum deviation angle = δ_m = 30°

we have to find the refractive index of the prism, that is, n

By using the formula of the angle of minimum deviation,

n = Sin((A+δ_m)/2)/Sin(A/2)

n = Sin ((60°+30°)/2)/Sin(60°/2)

n = Sin (90°/2)/Sin(60°/2)

n = Sin45°/Sin30°

n = 1.414

Example 3: The light rays passing through the beam gets deviated by 10°. If the angle of incidence is equal to the angle of emergence and its value is 40°. Find out the value of the angle of prism.

Solution: We have been given

i = angle of incidence = 40°

e = angle of emergence = i = 40°

δ = deviation angle = 10°

By using the formula for the angle of deviation

δ = i + e – A

or, δ +A = i + e

on substituting the value in this equation,

10° + A = 40° + 40°

A = 80° – 10°

A = 70°

Hence, the angle of prism = 70°

Sharing is caring!