Angle Between Two Vectors- Meaning, Formula, Examples

Angle Between Two Vectors: The angle between two vectors is one of the crucial concepts in physics as well as mathematics. Vectors are those quantities that have magnitude as well as direction. Many of the popular known physical quantities such as Force, Velocity, Electric Field, etc. are vector quantities. Apart from the vector quantities, other quantities are known as scalar quantities. These physical quantities only have magnitude and do not possess direction. Some of these quantities are power, distance, etc. As vectors have directions associated with them, angle plays an important role in vectors.

Angle Between Two Vectors

Just as a normal angle between two line segments are formed when they are joined end to end, the angle between two vectors are formed by joining their ends. In the graphical form, vectors consist of a head and a tail. The angle is formed when two vectors are joined from tail-to-tail. There are two different ways to find the angle formed between two vectors. It is important to note that the vector can take angles value in the range of acute angle, right angle, or obtuse angle, depending on the direction of the two vectors. Let us understanding this interesting concept by understanding its meaning through its definition and diagrams.

Angle Between Two Vectors Meaning

The meaning of the angle between the two vectors precisely mean the angle formed when the two vectors meet at the common point. As per the formal definition, the angle formed between the tails of two vectors is known as the angle between two vectors. When two vectors are joined through their tails, then the angle formed is said to be the angle between two vectors. In other words, an angle is created between two vectors when their tails are joined. We can recognize the tail of the vector just by viewing its graphical notation. The outcome of two vectors acting on a particle relies on the angle at which they are acting. Therefore, it is crucial to understand the angle between them. The following diagram shows the valid and invalid angle formation between two vectors.

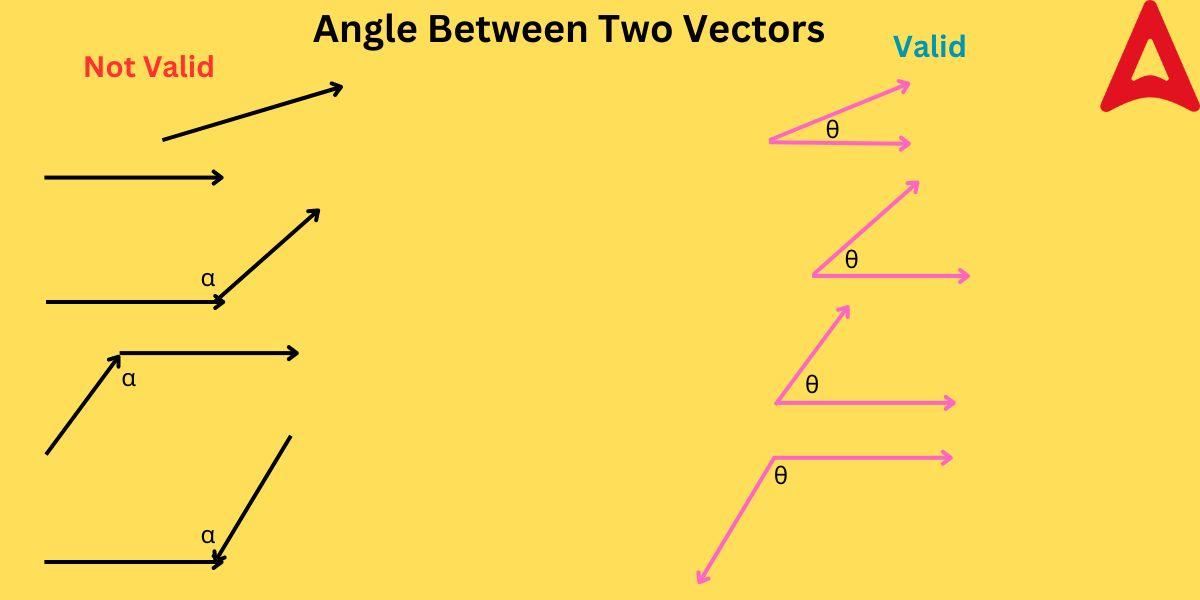
As you can observe in the above figure, in the left hand side of the diagram, the vectors are either not joined or they are not joined tail-to tail. Hence, they cannot be termed as the valid angle between the two vectors. Whereas, on the right hand side of the diagram, the two vectors are joined tail-to-tail. Hence, they are forming a valid angle between the two vector quantities. They have been colored in pink color in the diagram and the angle between them is given to be θ.

Angle Between Two Vectors

Vector Symbol Notation

Vectors can be represented either in graphical form or equation form (co-ordinate system form). In graphical form, the vector symbol is denoted by an arrow (→). The part with the pointed shape is known as the head of the vector while the other part is known as the tail of the vector. In the equation form, the vector magnitude is accompanied by the direction vector. The direction vector are unitless vector that has a magnitude of 1. Using these unit vectors, a vector quantity can be represented both in a 2D plane and a 3D plane. The unit vector is denoted by a cap (^) on its head. For example, “i” unit vector denotes the x-axis, “j” unit vector denotes the y-axis, and “k” unit vector denotes the z-axis.

Angle Between Two Vectors Diagram

The angle between any two vectors is said to exist if they are joined tail-to-tail. The same concept can be best understood by the diagram given below:

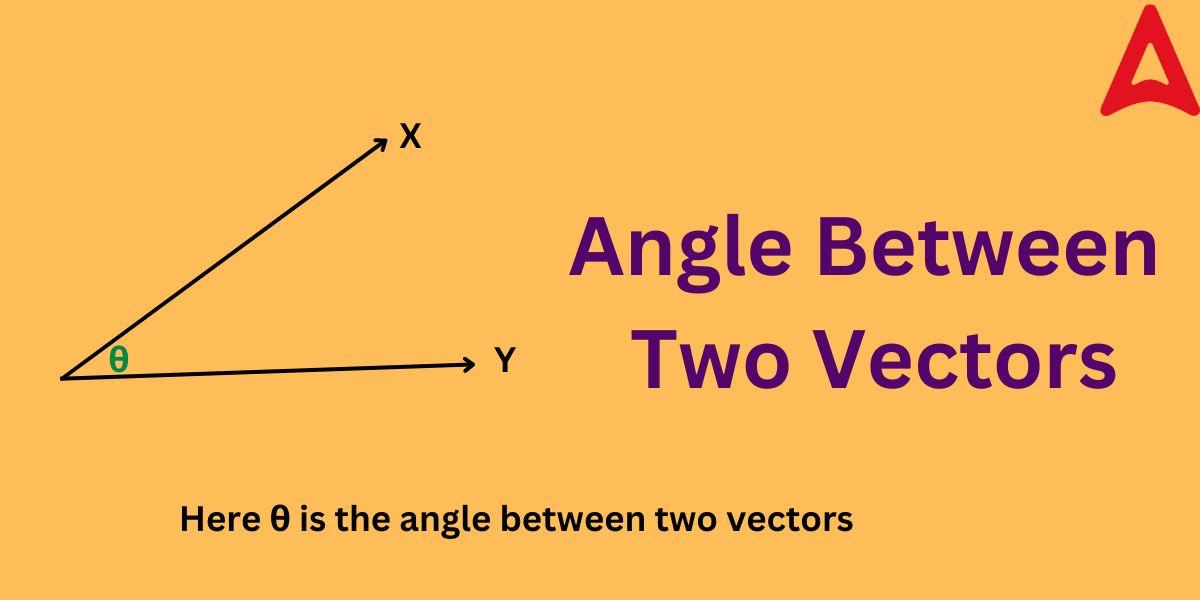
As shown in the above figure, two vectors A and B are joined tail-to-tail to form an angle θ. This θ angle can be termed as the angle between two vectors.

Angle Between Two Vectors Formula

The angle formed between two vectors is important as it is used in determining the effect of the resultant of the two vectors. There are two formulas used to find the angle existing between two vectors. These two formulas are: Dot Product and Cross Product. Let us discuss both these formula one-by-one.

Angle Between Two Vectors Applying Dot Product

The angle between two vectors can be found using the dot product. The . (dot) symbol is used to denoted the dot product. The dot product is also known as scalar product.

The angle formed by two vectors using dot product is given by:

θ = Cos^-1 [(a . b)/(|a| |b|)]

where, θ = angle formed between two vectors

|a| = magnitude of vector a

|b| = magnitude of vector b

Angle Between Two Vectors Applying Cross Product

The another method to find the angle created between two vectors is the cross product. It is denoted by the symbol cross (x), hence the name cross product. It is also known as the vector product.

The angle formed between two vectors using the cross product is given by:

θ = Sin^-1 [|a| x |b|)/(|a| |b|)]

where, θ = angle formed between two vectors

|a| = magnitude of vector a

|b| = magnitude of vector b

Angle Between Two Vectors in 2D and 3D

Two vectors can be found either in 2D plane or a 3D plane. The angle between both of them can be found using the formula mentioned above either in 2D plane or 3D plane. The vectors in 3D plane will contain three unit vectors, namely i, j, and k. While the vectors in 2D plane will contain only i and j unit vectors. Using the dot product and vector’s magnitudes, one can find the angle between them both in 2D as well as 3D plane.

Some examples of the vector in 2D plane are: 2i+3j, 7i+10j, 8i+9j, etc.

The examples of vectors in 3D plane are: 2i+3j+4k, 16i+9j+k, 4i+3k, etc.

How to Find the Angle Between Two Vectors

One can find the angle between two vectors using the following steps:

Step 1: First check whether the two vectors form a vector angle or not

Step 2: If they are not joined tail-to-tail, then shift the vector parallelly so that they are joined tail-to-tail

Step 3: Once the angle is formed, find the magnitude of the individual vectors

Step 4: Use the dot product or cross product formula given above to find the angle formed between two vectors

It is always advisable to go for dot product to avoid ambiguity in finding the desired angle.

Angle Between Two Vectors Properties

The angle formed between two vectors exhibit very interesting properties. These properties are helpful in understanding various concepts related to vectors. Some of these properties are:

• The value of the angle between two vectors always range from 0° to 180°
• Two equal vectors always subtend an angle of 0°
• The angle between two parallel vectors is always 0
• The angle between two positive vectors range from 0° to 90°
• If the dot product of two vectors is positive, then the angle between them must be more than 0° and less than 90°
• Unit vectors subtend angle of 0° with one another
• If the dot product of two vectors is negative, then the angle between them must be more than 90° and less than equal to 180°

Angle Between Two Vectors Examples

Some of the solved examples of the angle between two vectors is given below. These solved questions will be helpful for students who have opted for physics in class 11. By going through these solved examples, students will get a better understanding of the subject.

Example 1: Two vectors i-2j and -2i+j are joined together tail-to-tai. What will be the angle between these two vectors?

Solution: As we know, the angle between two vectors is given by:

θ = Cos^-1 [(a . b)/(|a| |b|)]

Given,

a = i-2j

b = -2i+j

a . b = 1 x (-2) + (-2) x 1

a . b = -2 – 2

a . b= -4

|a| = √(1)² + (-2)²

|a| = √1 + 4

|a| = √5

|b| = √(-2)² + (1)²

|b| = √5

on substituting these values in the equation, we get

θ = Cos^-1 (-4/√5 x √5)

θ = Cos^-1 (-4/5)

Example 2: Find the angle created by two vectors whose dimensions are 2i + 4j + k and 3i – j – k.

Solution- Given:

a = 2i+4j+k

b = 3i-j-k

By using the formula for the angle between two vectors,

θ = Cos^-1 [(a . b)/(|a| |b|)]

a . b = 2 x 3 + 4 x (-1) + 1 x (-1)

a . b = 6 -4 -1

a . b= 1

|a| = √(2)² + (4)² + (1)²

|a| = √4 + 16 + 1

|a| = √21

|b| = √(3)² + (-1)² + (-1)²

|b| = √9 + 1 + 1

|b| = √11

on substituting these values in the equation, we get

θ = Cos^-1 (1/√21 x √11)

θ = Cos^-1 (1/√231)

Example 3: If the cross product of two vectors is equal to 1/2, then what will be the angle between them?

Solution: As we know the cross product is given by:

Sinθ = [|a| x |b|)/(|a| |b|)]

given [|a| x |b|)/(|a| |b|)] = 1/2

putting this value in the above equation

Sinθ = 1/2

Sinθ = Sin30°

Hence, θ = 30°

Sharing is caring!